Skip to main content
SpringerLink
Log in

On the Role of Involutions in the Discontinuous Galerkin Discretization of Maxwell and Magnetohydrodynamic Systems

  • Conference paper
Compatible Spatial Discretizations

Part of the book series: The IMA Volumes in Mathematics and its Applications ((IMA,volume 142))

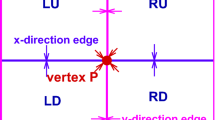
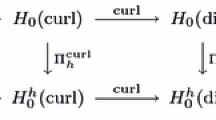
Abstract

The role of involutions in energy stability of the discontinuous Galerkin (DG) discretization of Maxwell and magnetohydrodynamic (MHD) systems is examined. Important differences are identified in the symmetrization of the Maxwell and MHD systems that impact the construction of energy stable discretizations using the DG method. Specifically, general sufficient conditions to be imposed on the DG numerical flux and approximation space are given so that energy stability is retained. These sufficient conditions reveal the favorable energy consequence of imposing continuity in the normal component of the magnetic induction field at interelement boundaries for MHD discretizations. Counterintuitively, this condition is not required for stability of Maxwell discretizations using the discontinuous Galerkin method.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 169.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Preview

Unable to display preview. Download preview PDF.

Unable to display preview. Download preview PDF.

Similar content being viewed by others

References

  1. T.J. Barth. Numerical methods for gasdynamic systems on unstructured meshes. In Kröner, Ohlberger, and Rohde, editors, An Introduction to Recent Developments in Theory and Numerics for Conservation Laws, volume 5 of Lecture Notes in Computational Science and Engineering, pages 195–285. Springer-Verlag, Heidelberg, 1998.

    Google Scholar 

  2. T.J. Barth. Simplified discontinuous Galerkin methods for systems of conservation laws with convex extension. In Cockburn, Karniadakis, and Shu, editors, Discontinuous Galerkin Methods, Volume 11 of Lecture Notes in Computational Science and Engineering. Springer-Verlag, Heidelberg, 1999.

    Google Scholar 

  3. T.J. Barth. On the discontinuous Galerkin approximation of compressible ideal magnetohydrodynamics I: Energy stable discretizations. In preparation, 2005.

    Google Scholar 

  4. J.U. Brackbill and D.C. Barnes. The effect of nonzero Δ · B on the numerical solution of the magnetohydrodynamic equations. J. Comp. Phys., 35:426–430, 1980.

    Article  MathSciNet  Google Scholar 

  5. N. Besse and D. Kröner. Convergence of locally divergence-free discontinuous Galerkin methods for the induction equations of the MHD system. Technical Report Submitted to M2AN, Wolfgang Pauli Institute, Austria, 2004.

    Google Scholar 

  6. G. Boillat. Involutions des systéms conservatifs. C. R. Acad. Sci. Paris, Sere I, 307:891–894, 1988.

    MathSciNet  Google Scholar 

  7. A. Bossavit. Computational Electromagnetism, Variational Formulations, Complementarity, Edge Elements. Academic Press, San Diego, 1998.

    MATH  Google Scholar 

  8. P.B. Bochev and A.C. Robinson. Matching algorithms and physics: Exact sequences of finite element spaces. In D. Estep and S. Tavener, editors, Collected Lectures on the Preservation of Stability Under Discretization, Philadephia, 2002. SIAM.

    Google Scholar 

  9. B. Cockburn, S. Hou, and C.W. Shu. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws IV: The multidimensional case. Math. Comp., 54:545–581, 1990.

    Article  MathSciNet  Google Scholar 

  10. B. Cockburn, S.Y. Lin, and C.W. Shu. TVB Runge-Kutta local projection discontinuous Galerkin finite element method for conservation laws III: One dimensional systems. J. Comp. Phys., 84:90–113, 1989.

    Article  MathSciNet  Google Scholar 

  11. B. Cockburn, F. Li, and C.W. Shu. Locally divergence-free discontinuous Galerkin methods for Maxwell equations. J. Comp. Phys., 194:588–610, 2004.

    Article  MathSciNet  Google Scholar 

  12. B. Cockburn and C.W. Shu. The Runge-Kutta discontinuous Galerkin method for conservation laws V: Multidimensional systems. Technical Report 201737, Institite for Computer Applications in Science and Engineering (ICASE), NASA Langley R.C., 1997.

    Google Scholar 

  13. A. Csik. Upwind Residual Distribution Schemes for General Hyperbolic Conservation Laws with Application to Ideal Magnetohydrodynamics. PhD thesis, University of Leuven, Belgium, 2002.

    Google Scholar 

  14. C. Dafermos. Quasilinear hyperbolic systems with involutions. Arch. Rational Mech. Anal., 106:373–389, 1986.

    Article  MathSciNet  Google Scholar 

  15. A. Dedner, F. Kemm, D. Kröner, C.-D. Munz, T. Schnitner, and M. Wesenberg. Hyperbolic divergence cleaning for the MHD equations. J. Comp. Phys., 175:645–673, 2002.

    Article  Google Scholar 

  16. B. Einfeldt, C. Munz, P. Roe, and B. Sjögreen. On Godunov-type methods near low densities. J. Comp. Phys., 92:273–295, 1992.

    Article  Google Scholar 

  17. S.K. Godunov. An interesting class of quasilinear systems. Dokl. Akad. Nauk. SSSR, 139:521–523, 1961.

    MathSciNet  Google Scholar 

  18. S.K. Godunov. The symmetric form of magnetohydrodynamics equation. Num. Meth. Mech. Cont. Media, 1:26–34, 1972.

    Google Scholar 

  19. A. Harten, P.D. Lax, and B. van Leer. On upstream differencing and Godunov-type schemes for hyperbolic conservation laws. SIAM Rev., 25:35–61, 1983.

    Article  MathSciNet  Google Scholar 

  20. J.M. Hyman and M. Shashkov. Mimetic discretizations for Maxwell’s equations. J. Comp. Phys., 151:881–909, 1999.

    Article  MathSciNet  Google Scholar 

  21. J. Jaffre, C. Johnson, and A. Szepessy. Convergence of the discontinuous Galerkin finite element method for hyperbolic conservation laws. Math. Models and Methods in Appl. Sci., 5(3):367–386, 1995.

    Article  MathSciNet  Google Scholar 

  22. C. Johnson and J. Pitkäranta. An analysis of the discontinuous Galerkin method for a scalar hyperbolic equation. Math. Corny., 46:1–26, 1986.

    Article  Google Scholar 

  23. G. Jiang and C.-W. Shu. On a cell entropy inequality for discontinuous galerkin methods. Math. Corny., 62:531–538, 1994.

    Article  MathSciNet  Google Scholar 

  24. P. Lesaint and P.A. Raviart. On a finite element method for solving the neuton transport equation. In C. de Boor, editor, Mathematical Aspects of Finite Elements in Partial Differential Equations, pages 89–145. Academic Press, 1974.

    Google Scholar 

  25. M.L. Merriam. An Entropy-Based Approach to Nonlinear Stability. PhD thesis, Stanford University, 1988.

    Google Scholar 

  26. M.S. Mock. Systems of conservation laws of mixed type. J. Diff. Eqns., 37:70–88, 1980.

    Article  MathSciNet  Google Scholar 

  27. J.C. Nedelec. Mixed finite elements in ℝ3. Numer. Math., 35:315–341, 1980.

    Article  MathSciNet  Google Scholar 

  28. S. Osher. Riemann solvers, the entropy condition, and difference approximations. SIAM J. Numer. Anal, 21(2):217–235, 1984.

    Article  MathSciNet  Google Scholar 

  29. K.G. Powell. An approximate Riemann solver for magnetohydrodynamics (that works in more than one dimension). Technical Report 94-24, Institite for Computer Applications in Science and Engineering (ICASE), NASA Langley R.C., 1994.

    Google Scholar 

  30. W.H. Reed and T.R. Hill. Triangular mesh methods for the neutron transport equation. Technical Report LA-UR-73-479, Los Alamos National Laboratory, Los Alamos, New Mexico, 1973.

    Google Scholar 

  31. C.-W. Shu. Discontinuous Galerkin methods for convection-dominated problems. In Barth and Deconinck, editors, High-Order Discretization Methods in Computational Physics, Volume 9 of Lecture Notes in Computational Science and Engineering. Springer-Verlag, Heidelberg, 1999.

    Google Scholar 

  32. G. Tóth. The Δ · B = 0 constraint in shock-capturing magnetohydrodynamics codes. J. Comp. Phys., 161:605–652, 2000.

    Article  Google Scholar 

  33. K.S. Yee. Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media. IEEE Trans. Ant. Prop., AP-14:302–307, 1966.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. NASA Ames Research Center, M.S. T27A-1, Moffett Field, CA, 94035-1000, USA

    Timothy Barth

Authors
  1. Timothy Barth
    View author publications

    You can also search for this author in PubMed Google Scholar

Editor information

Editors and Affiliations

  1. Institute for Mathematics and its Applications, University of Minnesota, Minneapolis, MN, 55455, USA

    Douglas N. Arnold

  2. Computational Mathematics and Algorithms Department, Sandia National Laboratories, Alburquerque, NM, 87185-1110, USA

    Pavel B. Bochev  & Richard B. Lehoucq  & 

  3. Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA, 15213-3890, USA

    Roy A. Nicolaides

  4. Theoretical Division, Los Alamos National Laboratory, Los Alamos, NM, 87545, USA

    Mikhail Shashkov

Rights and permissions

Reprints and permissions

Copyright information

© 2006 Springer Science+Business Media, LLC

About this paper

Cite this paper

Barth, T. (2006). On the Role of Involutions in the Discontinuous Galerkin Discretization of Maxwell and Magnetohydrodynamic Systems. In: Arnold, D.N., Bochev, P.B., Lehoucq, R.B., Nicolaides, R.A., Shashkov, M. (eds) Compatible Spatial Discretizations. The IMA Volumes in Mathematics and its Applications, vol 142. Springer, New York, NY. https://doi.org/10.1007/0-387-38034-5_4

Download citation

Publish with us

Policies and ethics

Search

Navigation