Skip to main content
SpringerLink
Log in

Dynamic Increase Factor of Concrete Subjected to Compression and Tension by using Split Hopkinson Pressure Bar Setup: Overview

  • Published:
Mechanics of Solids Aims and scope Submit manuscript

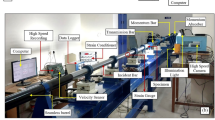
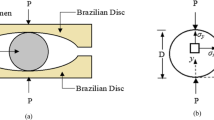
Abstract

The dynamic increase factor (DIF) for the dynamic compressive and tensile strength of concrete-like brittle materials subjected to impact and blast loading has been a broad subject of extensive investigation and debate for many years. The necessity of studying the dynamic behaviour of concrete-like brittle material is increasing daily for the analysis and design of building structures for safety and security purposes. In this context, this paper reviews and summarizes the dynamic increase factor obtained from experimental and numerical studies under compression and tension for their resistance under a high loading rate. Numerous researchers have conducted Split Hopkinson Pressure Bar (SHPB) experiments on concrete, mortar, and composite materials. They have proposed several empirical relationships between the strain rate and Dynamic Increase Factor (DIF). These DIF values, suitable for both compression and tension, have gained extensive acceptance in authoritative design guidelines and model codes for numerical simulation studies. Most of the DIF models followed the power low variation function, linear function, and polynomial function as a function of strain rate, but the trends of DIF models significantly varied from each other based on the experimental results. A few DIF models are available considering the effect of end friction confinement, lateral inertia confinement, porosity, specimen dimensions, and fiber content, as these factors also significantly influence the dynamic strength of materials. Additionally, the value suggested for the transition strain rate significantly varied in compression as well as in tension based on the experimental study. The transition strain rate for dynamic strength in compression is predominantly observed to be above 10 s–1, whereas, for tensile strength, the transition strain rate is approximately 1 s–1, described that the tensile behaviour of concrete is more sensitive to the strain rate.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.

Similar content being viewed by others

REFERENCES

  1. U. S. Lindholm, “High strain testing, part I: measurement of mechanical properties,” in Techniques of Metals Research, Ed by. R. F. Bunshah, Vol. 5 (Wiley Interscience, New York, 1971), pp. 199–271.

    Google Scholar 

  2. W. W. Chen and B. Song, “Conventional Kolsky bars,” in Split Hopkinson (Kolsky) Bar. Mechanical Engineering Series (Springer, Boston, 2010), pp. 1–35. https://doi.org/10.1007/978-1-4419-7982-7_1

    Book  Google Scholar 

  3. B. Song, K. Connelly, J. Korellis, et al., “Improved Kolsky-bar design for mechanical characterization of materials at high strain rates,” Meas. Sci. Technol. 20 (11), 115701 (2009). https://doi.org/10.1088/0957-0233/20/11/115701

  4. M. M. Khan and M. A. Iqbal, “Design, development, and calibration of split Hopkinson pressure bar system for Dynamic material characterization of concrete,” Int. J. Protect. Struct. (2023). https://doi.org/10.1177/20414196231155947

  5. C. A. Ross, J. W. Tedesco, and S. T. Kuennen, “Effects of strain rate on concrete strength,” Mater. J. 92 (1), 37–47 (1995). https://doi.org/10.14359/1175

    Article  Google Scholar 

  6. Q. M. Li, and H. Meng, “About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test,” Int. J. Solids Struct. 40 (2), 343–360 (2003). https://doi.org/10.1016/S0020-7683(02)00526-7

    Article  Google Scholar 

  7. T. J. Holmquist and G. R. Johnson, “A computational constitutive model for glass subjected to large strains, high strain rates and high pressures,” ASME J. Appl. Mech. 78 (5), 051003 (2011). https://doi.org/10.1115/1.4004326

  8. W. Riedel, Doctoral Dissertation in Engineering (Fraunhofer Institut für Kurzzeitdynamik, Ernst-Mach-Institut, Freiburg, 2000).

  9. W. Riedel, N. Kawai, and K. I. Kondo, “Numerical assessment for impact strength measurements in concrete materials,” Int. J. Impact Eng. 36 (2), 283–293 (2009). https://doi.org/10.1016/j.ijimpeng.2007.12.012

    Article  Google Scholar 

  10. D. C. Drucker and W. Prager, “Soil mechanics and plastic analysis for limit design,” Quart. Appl. Math. 10 (2), 157–165 (1952).

    Article  MathSciNet  Google Scholar 

  11. T. Jankowiak and T. Lodygowski, “Identification of parameters of concrete damage plasticity constitutive model,” Found. Civil Environ. Eng. 6 (1), 53–69 (2005).

    Google Scholar 

  12. M. A. Kamran and Iqbal, “A new material model for concrete subjected to high rate of loading,” Int. J. Impact Eng. (2023). https://doi.org/10.1016/j.ijimpeng.2023.104673

  13. X. Chen, S. Wu, and J. Zhou, “Experimental and modeling study of dynamic mechanical properties of cement paste, mortar and concrete,” Constr. Build. Mater. 47, 419–430 (2013). https://doi.org/10.1016/j.conbuildmat.2013.05.063

    Article  ADS  Google Scholar 

  14. S. Lee, K. M. Kim, J. Park, and J. Y. Cho, “Pure rate effect on the concrete compressive strength in the split Hopkinson pressure bar test,” Int. J. Impact Eng. 113, 191–202 (2018). https://doi.org/10.1016/j.ijimpeng.2017.11.015

    Article  Google Scholar 

  15. M. K. Khan, M. A. Iqbal, V. Bratov, et al., “An investigation of the ballistic performance of independent ceramic target,” Thin-Walled Struct. 154, 106784 (2020). https://doi.org/10.1016/j.tws.2020.106784

  16. M. K. Khan and M. A. Iqbal, “Failure and fragmentation of ceramic target with varying geometric configuration under ballistic impact,” Ceram. Int. 48 (18), 26147–26167 (2022). https://doi.org/10.1016/j.ceramint.2022.05.297

    Article  CAS  Google Scholar 

  17. Y. B. Guo, G. F. Gao, L. Jing, and V. P. W. Shim, “Response of high-strength concrete to dynamic compressive loading,” Int. J. Impact Eng. 108, 114–135 (2017). https://doi.org/10.1016/j.ijimpeng.2017.04.015

    Article  Google Scholar 

  18. E. A. Flores-Johnson and Q. M. Li, “Structural effects on compressive strength enhancement of concrete-like materials in a split Hopkinson pressure bar test,” Int. J. Impact Eng. 109, 408–418 (2017). https://doi.org/10.1016/j.ijimpeng.2017.08.003

    Article  Google Scholar 

  19. Comite Euro-International du Beton, CEB-FIP Model Code 1990: Design Code (Thomas Telford, London, 1993).

    Book  Google Scholar 

  20. Y. Hao, H. Hao, G. P. Jiang, and Y. Zhou, “Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests,” Cem. Concr. Res. 52, 63–70 (2013). https://doi.org/10.1016/j.cemconres.2013.05.008

    Article  CAS  Google Scholar 

  21. Code Requirements for Nuclear Safety-Related Concrete Structures and Commentary, Model Code ACI 349-13 (ACI Committee, 2014).

  22. Structures to Resist the Effects of Accidental Explosions, UFC 3-340-02, Unified Facilities Criteria (UFC) (United States Department of Defense, 2008).

  23. Model Code, 2010, First Complete Draft, Vol. 1 (FIB, 2010).

  24. J. Hopkinson, “On the rupture of iron wire by a blow,” Proc. Literary Phil. Soc. Manch. 1, 40–45 (1872).

    Google Scholar 

  25. H. Kolsky, “An investigation of the mechanical properties of materials at very high rates of loading,” Proc. Phys. Soc. B 62 (11), 676 (1949). https://doi.org/10.1088/0370-1301/62/11/302

    Article  ADS  Google Scholar 

  26. B. Song, K. Connelly, J. Korellis, et al., “Improvement in Kolsky-bar design for mechanical characterization of materials at high strain rates,” Meas. Sci. Technol. 20, 115701 (2009). https://doi.org/10.1088/0957-0233/20/11/115701

  27. J. W. Tedesco and C. A. Ross, “Experimental and numerical analysis of high strain rate splitting-tensile tests,” Mater. J. 90 (2), 162–169 (1993). https://doi.org/10.14359/4013

    Article  CAS  Google Scholar 

  28. J. W. Tedesco, J. C. Powell, C. A. Ross, and M. L. Hughes, “A strain-rate-dependent concrete material model for ADINA,” Comp. Struct. 64 (5–6), 1053–1067 (1997). https://doi.org/10.1016/S0045-7949(97)00018-7

    Article  Google Scholar 

  29. H. Schuler, C. Mayrhofer, and K. Thoma, “Spall experiments for the measurement of the tensile strength and fracture energy of concrete at high strain rates,” Int. J. Impact Eng. 32 (10), 1635-1650 (2006). https://doi.org/10.1016/j.ijimpeng.2005.01.010

    Article  Google Scholar 

  30. K. Fujikake, K. Uebayashi, T. Ohno, et al., “Formulation of an orthotropic constitutive model for concrete materials under high strain rates and tri-axial stress states,” J. Mat. Conc. Struct. Pave. 50 (669), 109–23 (2001). https://doi.org/10.2208/jscej.2001.669_109

    Article  Google Scholar 

  31. T. Hartmann, A. Pietzsch, and N. Gebbeken, “A hydrocode material model for concrete,” Int. J. Protect. Struct. 1 (4), 443–68 (2010). https://doi.org/10.1260/2041-4196.1.4.443

    Article  Google Scholar 

  32. J. W. Tedesco and C. A. Ross, “Strain-rate-dependent constitutive equations for concrete,” ASME J. Pressure Vessel Technol. 120 (4), 398–405 (1998). https://doi.org/10.1115/1.2842350

    Article  Google Scholar 

  33. Y. Guo, G. Gao, L. Jing, and V. Shim, “Response of high-strength concrete to dynamic compressive loading,” Int. J. Impact Eng. 108, 114–135 (2017). https://doi.org/10.1016/j.ijimpeng.2017.04.015

    Article  Google Scholar 

  34. T. Ngo, P. Mendis, and T. Krauthammer, “Behavior of ultrahigh-strength prestressed concrete panels subjected to blast loading,” J. Struct. Eng. 133, 1582–1590 (2007). https://doi.org/10.1061/(ASCE)0733-9445(2007)133:11(1582)

    Article  Google Scholar 

  35. Y. Al-Salloum, T. Almusallam, S. M. Ibrahim, et al. “Rate dependent behavior and modeling of concrete based on SHPB experiments,” Cem. Concr. Compos. 55, 34–44 (2015). https://doi.org/10.1016/j.cemconcomp.2014.07.011

    Article  CAS  Google Scholar 

  36. Y. Lu and K. Xu, “Modelling of dynamic behaviour of concrete materials under blast loading,” Int. J. Solids Struct. 41(1), 131–43 (2004). https://doi.org/10.1016/j.ijsolstr.2003.09.019

    Article  CAS  Google Scholar 

  37. D. L. Grote, S. W. Park, and M. Zhou, “Dynamic behavior of concrete at high strain rates and pressures: I. experimental characterization,” Int. J. Impact Eng. 25 (9), 869–886 (2001). https://doi.org/10.1016/S0734-743X(01)00020-3

    Article  Google Scholar 

  38. Q. M. Li and H. Meng, “About the dynamic strength enhancement of concrete-like materials in a split Hopkinson pressure bar test,” Int. J. Solids Struct. 40 (2), 343–360 (2003). https://doi.org/10.1016/S0020-7683(02)00526-7

    Article  Google Scholar 

  39. X. Q. Zhou and H. Hao, “Modeling of compressive behaviour of concrete-like materials at high strain rate,” Int. J. Solids Struct. 45 (17), 4648–4661 (2008). https://doi.org/10.1016/S0020-7683(02)00526-7

    Article  Google Scholar 

  40. M. Katayama, M. Itoh, S. Tamura, et al., “Numerical analysis method for the RC and geological structures subjected to extreme loading by energetic materials,” Int. J. Impact Eng. 34, 1546–1561 (2007).

    Article  Google Scholar 

  41. Y. Hao, H. Hao, and Z. X. Li, “Influence of end friction confinement on impact tests of concrete material at high strain rate,” Int. J. Impact Eng. 60, 82–106 (2013). https://doi.org/10.1016/j.ijimpeng.2013.04.008

    Article  Google Scholar 

  42. Y.F. Hao and H. Hao, “Numerical evaluation of the influence of aggregates on concrete compressive strength at high strain rate,” Int. J. Protect. Struct. 2, 177–206 (2011). https://doi.org/10.1260/2041-4196.2.2.177

    Article  Google Scholar 

  43. Y.F. Hao, H. Hao, G.P. Jiang, and Y. Zhou, “Experimental confirmation of some factors influencing dynamic concrete compressive strengths in high-speed impact tests,” Cem. Concr. Res. 52, 63–70 (2013). https://doi.org/10.1016/j.cemconres.2013.05.008

    Article  CAS  Google Scholar 

  44. S. Ahmad, P. Bhargava, A. Chourasia, and A. Usmani, “Effect of elevated temperatures on the shear-friction behaviour of concrete: Experimental and analytical study,” Eng. Struct. 225, 111305 (2020). https://doi.org/10.1016/j.engstruct.2020.111305

  45. S. Ahmad, P. Bhargava, and N. M. Bhandari, “Evaluation of shear transfer capacity of reinforced concrete exposed to fire,” IOP Conf. Ser.: Earth Environ. Sci. 140 012146 (2018). https://doi.org/10.1088/1755-1315/140/1/012146

  46. S. Ahmad, P. Bhargava, and A. Chourasia, “Direct shear failure in concrete joints exposed to elevated temperatures,” Struct. 27, 1851–1859 (2020). https://doi.org/10.1016/j.istruc.2020.07.074

    Article  Google Scholar 

  47. S. Ahmad, P. Bhargava, A. Chourasia, and M. Ju, “Residual shear strength of reinforced concrete slender beams without transverse reinforcement after elevated temperatures,” Eng. Struct. 237, 112163 (2021). https://doi.org/10.1016/j.engstruct.2021.112163

  48. Fib Model Code for Concrete Structures 2010 (FIB, Lausanne, 2013).

  49. L. J. Malvar and C. A. Ross, “Review of strain rate effects for concrete in tension,” ACI Mater. J. 95, 735–739 (1998).

    CAS  Google Scholar 

  50. P. Soroushian, K. B. Choi, and A. Alhamad, “Dynamic constitutive behavior of concrete,” Int. J. Proc. 83 (2), 251–259 (1986).

    Google Scholar 

  51. K. Komlos, “Investigation of rheological properties of concrete in uniaxial tension,” Mater. Test. 12 (9), 300–304 (1970). https://doi.org/10.1515/mt-1970-120902

    Article  ADS  Google Scholar 

  52. S. Xiao, H. Li, and P. J. M. Monteiro, “Influence of strain rates and load histories on the tensile damage behaviour of concrete,” Mag. Concr. Res. 62 (12), 887–894 (2010). https://doi.org/10.1680/macr.2010.62.12.887

    Article  Google Scholar 

  53. S. Panchal, S. Sharma, M. M. Khan, et al., “Effect of glass reinforcement and glass powder on the characteristics of concrete,” Int. J. Civil Eng. Technol. 8 (3), 637–647 (2017).

    Google Scholar 

  54. Kamran and M. A. Iqbal, “The ballistic evaluation of plain, reinforced and reinforced–prestressed concrete,” Thin-Walled Struct. 179, 109707 (2022). https://doi.org/10.1016/j.tws.2022.109707

Download references

ACKNOWLEDGMENTS

The authors express their gratitude to the Indian Institute of Technology Roorkee, India, and the financial assistantship from the Ministry of Human Resource and Development (MHRD), Government of India.

Funding

No funding was received for conducting this study.

Author information

Authors and Affiliations

  1. Civil Engineering Department, Indian Institute of Technology Roorkee, 247667, Roorkee, India

    M. M. Khan & M. A. Iqbal

Authors
  1. M. M. Khan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. A. Iqbal
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to M. M. Khan or M. A. Iqbal.

Ethics declarations

CONFLICT OF INTEREST

The authors of this work declare that they have no conflicts of interest.

DECLARATION

All authors have been confirming their approval for publication and declare no conflicts of interest among them.

Additional information

Publisher’s Note.

Allerton Press remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Khan, M.M., Iqbal, M.A. Dynamic Increase Factor of Concrete Subjected to Compression and Tension by using Split Hopkinson Pressure Bar Setup: Overview. Mech. Solids 58, 2115–2131 (2023). https://doi.org/10.3103/S0025654423601064

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S0025654423601064

Keywords:

Search

Navigation