Skip to main content
SpringerLink
Log in

Optimal Control Selection for Stabilizing the Inverted Pendulum Problem Using Neural Network Method

  • Published:
Optical Memory and Neural Networks Aims and scope Submit manuscript

Abstract—

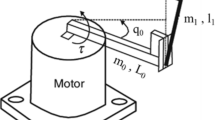
The task of managing unstable systems is a critically important management problem, as an unstable object can pose significant danger to humans and the environment when it fails. In this paper, a neural network was trained to determine the optimal control for an unstable system, based on a comparative analysis of two control methods: the implicit Euler method and the linearization method. This neural network identifies the optimal control based on the position of a point on the phase plane.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.
Fig. 9.
Fig. 10.
Fig. 11.
Fig. 12.

Similar content being viewed by others

REFERENCES

  1. Paredes, V.C. and Hereid, A., Resolved motion control for 3D underactuated bipedal walking using linear inverted pendulum dynamics and neural adaptation, 2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Kyoto, Japan, 2022, pp. 6761–6767. https://doi.org/10.1109/IROS47612.2022.9982009

  2. Shanmugam, L., Mani, P., and Joo, Y.H., Stabilization of event-triggered-based neural network control system and its application to wind power generation systems, IET Control Theory Appl., 2020, vol. 14, no. 10, pp. 1321–1333. https://doi.org/10.1049/iet-cta.2019.0246

    Article  MathSciNet  Google Scholar 

  3. Mukhtar Fatihu Hamza, Hwa Jen Yap, Imtiaz Ahmed Choudhury, Abdulbasid Ismail Isa, Aminu Yahaya Zimit, and Tufan Kumbasar, Current development on using Rotary Inverted Pendulum as a benchmark for testing linear and nonlinear control algorithms, Mech. Syst. Signal Process., 2019, no. 116, pp. 347–369. https://doi.org/10.1016/j.ymssp.2018.06.054

  4. Kozlov, D.S. and Tiumentsev, Y.V., Neural network based semi-empirical models for dynamical systems described by differential-algebraic equations, Opt. Mem. Neural Networks, 2015 no. 24, pp. 279–287. https://doi.org/10.3103/S1060992X15040049

  5. Kolganov, P.A., Kondratiev, A.I., Tiumentsev, A.Y., et al., Neural network nonlinear adaptive fault tolerant motion control for unmanned aerial vehicles, Opt. Mem. Neural Networks, 2022, no. 31, pp. 1–15. https://doi.org/10.3103/S1060992X22010064

  6. Liu, Zhitai; Gao, Huijun; Yu, Xinghu; Lin, Weiyang, Qiu, Jianbin, Rodriguez-Andina, Juan J., Qu, Dongsheng, B-spline wavelet neural network-based adaptive control for linear motor-driven systems via a novel gradient descent algorithm, IEEE Trans. Ind. Electron., 2023, pp. 1–10, https://doi.org/10.1109/TIE.2023.3260318

  7. Bottcher, L. and Asikis, T., Near-optimal control of dynamical systems with neural ordinary differential equations, Mach. Learn.: Sci. Technol., 2022, no. 3, 045004

  8. Lim, H.-K., Kim, J.-B., Kim, C.-M., Hwang, G.-Y., Choi, H.-B., and Han, Y.-H., Federated reinforcement learning for controlling multiple rotary inverted pendulums in edge computing environments, 2020 International Conference on Artificial Intelligence in Information and Communication (ICAIIC), Fukuoka, Japan, 2020, pp. 463–464. https://doi.org/10.1109/ICAIIC48513.2020.9065233

  9. Yi Ming Ren, Alhajeri, M.S., Junwei Luo, Scarlett Chen, Fahim Abdullah, Zhe Wu, and Christofides, P.D., A tutorial review of neural network modeling approaches for model predictive control, Comput. Chem. Eng., 2022, vol. 165, 107956, doi.org/https://doi.org/10.1016/j.compchemeng.2022.107956

    Article  Google Scholar 

  10. Ronzhina, M.I. and Manita, L.A., Spiral-like extremals near a singular surface in a rocket control problem, Regular Chaotic Dyn., 2023, vol. 28, no. 2, pp. 148–161.

    Article  MathSciNet  MATH  Google Scholar 

  11. Ma, L. and Kong, Q., Optimal shortcuts to adiabatic control by lagrange mechanics. Entropy, 2023, vol. 25, no. 5, p. 719.

    Article  MathSciNet  Google Scholar 

  12. Pontryagin, L.S., Mathematical theory of optimal processes, Classics of Soviet Mathematics, CRC Press, 1987.

    Google Scholar 

  13. Lazovskaya, T. and Tarkhov, D., Multilayer neural network models based on grid methods, IOP Conf. Ser.: Mater. Sci. Eng., vol. 158, no. 1, p. 012061.

  14. Tarkhov, D., Lazovskaya, T., and Malykhina, G., Constructing physics-informed neural networks with architecture based on analytical modification of numerical methods by solving the problem of modelling processes in a chemical reactor, Sensors, 2023, vol. 23, p. 663. https://doi.org/10.3390/s23020663

    Article  Google Scholar 

  15. Hairer, E., Norsett, S.P, and Wanner, G., Solving Ordinary Differential Equations I: Nonstiff Problems, Springer Science & Business Media, 2008.

    MATH  Google Scholar 

  16. Degilevich, E.A. et al., Comparative testing of the neural network and semi-empirical method on the stabilization problem of inverted pendulum, in Advances in Neural Computation, Machine Learning, and Cognitive Research II. NEUROINFORMATICS 2018, Studies in Computational Intelligence, Kryzhanovsky, B., Dunin-Barkowski, W., Redko, V., and Tiumentsev, Y., Eds., 2019, p. 799. https://doi.org/10.1007/978-3-030-01328-8_10

Download references

Funding

This work was supported by the Russian Science Foundation, grant no. 22-21-20004, https://rscf.ru/project/22-21-20004/.

Author information

Authors and Affiliations

  1. Peter the Great St. Petersburg Polytechnic University, 195251, St. Petersburg, Russia

    D. A. Tarkhov, D. A. Lavygin, O. A. Skripkin, M. D. Zakirova & T. V. Lazovskaya

Authors
  1. D. A. Tarkhov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. D. A. Lavygin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. O. A. Skripkin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. M. D. Zakirova
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. T. V. Lazovskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to D. A. Tarkhov.

Ethics declarations

The authors of this work declare that they have no conflicts of interest.

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tarkhov, D.A., Lavygin, D.A., Skripkin, O.A. et al. Optimal Control Selection for Stabilizing the Inverted Pendulum Problem Using Neural Network Method. Opt. Mem. Neural Networks 32 (Suppl 2), S214–S225 (2023). https://doi.org/10.3103/S1060992X23060115

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.3103/S1060992X23060115

Keywords:

Search

Navigation