Numerical model of hepatic glycogen phosphorylase regulation by nonlinear interdependent dynamics of calcium and $IP_{3}$

Abstract

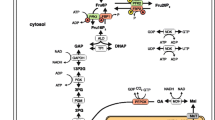
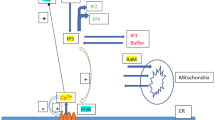
The liver’s primary function is to integrate various signals to retain stable blood glucose levels. Glycogenolysis, gluconeogenesis, and other metabolic processes are regulated by circulating hormones via calcium-dependent signaling. In this paper, the influence of calcium concentration on glycogen phosphorylase in hepatocytes is investigated utilizing a numerical approach. The system comprising two nonlinear reaction-diffusion equations for calcium and $IP_{3}$, respectively, has been coupled to propose a mathematical model. The temporal equation of the fraction of active glycogen phosphorylase ($\phi$) is also incorporated into the model. The finite volume and the Crank Nicolson methods are implemented along spatial and temporal dimensions, while the Gauss-Seidel method is employed to simplify the resulting nonlinear equations. The impact of calcium influx, EGTA buffer concentration, SERCA pump rate constant, and leak flux constant on the $\phi$ has been studied. It has been observed that interdependent calcium and $IP_{3}$ dynamics have a crucial role in controlling the blood glucose level. Any dysregulation of calcium and $IP_{3}$ processes can lead to the dysregulation of glycogen phosphorylase. This may lead to hyperglycemia or hypoglycemia.

Graphical abstract

Appendix: model equations summary

Solving space integration of Eq. (23) we get,

$$\begin{aligned}&\frac{\delta x}{D_{Ca}}\int ^{t+\Delta t}_t\frac{\partial C_{G}}{\partial t} dt=\int ^{t+\Delta t}_{t}\left[ \left( \frac{\partial C}{\partial x} \right) _{e}-\left( \frac{\partial C}{\partial x} \right) _{w} \right] dt-a\int ^{t+\Delta t}_{t}C_{G}\delta x dt+a C_{{\infty }} \delta x \delta t \nonumber \\&\qquad +\delta x\int ^{t+\Delta t}_{t}\frac{ \lambda _{IP3R}}{D_{Ca}V_{C}} \left( \dfrac{(P_{c})_{G}}{(P_{c})_{G}+K_{IP3}}\dfrac{C_{G}}{C_{G}+K_{Act}}\right) ^{3}\left( \dfrac{K_{Inh}}{K_{Inh}+C_{G}}\right) ^{3}\nonumber \\&\quad \left( \dfrac{C_{T}-V_{C}C_{G}}{V_{E}} -C_{G}\right) dt +\delta x\int ^{t+\Delta t}_{t}\frac{\lambda _{LK}}{D_{Ca}V_{C}}\left( \dfrac{C_{T}-V_{C}C_{G}}{V_{E}}-C_{G}\right) dt \nonumber \\&\qquad -\delta x\int ^{t+\Delta t}_{t}\frac{\lambda _{SERCA}}{D_{Ca}V_{C}}\dfrac{C_{G}^{2}}{K_{SERCA}^{2}+C_{G}^{2}} dt. \end{aligned}$$

(28)

The time integral is simplified by using weighted parameter $\Psi$, where $\Psi \in \left[ 0, 1 \right]$.

$$\begin{aligned}&\frac{\delta x}{D_{Ca}} [C_{G}-C_{G}^{0}]= \Psi \left[ \frac{C_{E}-C_{G}}{\delta x} -\frac{C_{G}-C_{W}}{\delta x}\right] \Delta t \nonumber \\&\qquad +(1-\Psi ) \left[ \frac{C_{E}^{0}-C_{G}^{0}}{\delta x} -\frac{C_{G}^{0}-C_{W}^{0}}{\delta x}\right] \Delta t-a\delta x[\Psi C_{G}+(1-\Psi )C_{G}^{0}]\Delta t+a C_{{\infty }} \delta x \delta t \nonumber \\&\qquad + \delta x \frac{ \lambda _{IP3R}}{D_{Ca}V_{C}}.\Psi \left( \dfrac{(P_{c})_{G}}{(P_{c})_{G}+K_{IP3}}\dfrac{C_{G}}{C_{G}+K_{Act}}\right) ^{3}\left( \dfrac{K_{Inh}}{K_{Inh}+C_{G}}\right) ^{3}\left( \dfrac{C_{T}-V_{C}C_{G}}{V_{E}} -C_{G}\right) \Delta t\nonumber \\&\qquad +(1-\Psi ) \left( \dfrac{(P_{c})_{G}^{0}}{(P_{c})_{G}^{0}+K_{IP3}}\dfrac{C_{G}^{0}}{C_{G}^{0}+K_{Act}}\right) ^{3}\left( \dfrac{K_{Inh}}{K_{Inh}+C_{G}^{0}}\right) ^{3}\left( \dfrac{C_{T}-V_{C}C_{G}^{0}}{V_{E}} -C_{G}^{0}\right) \Delta t \nonumber \\&\qquad +\delta x.\Psi \left[ \frac{\lambda _{LK}}{D_{Ca}V_{C}}\left( \dfrac{C_{T}-V_{C}C_{G}}{V_{E}}-C_{G}\right) -\frac{\lambda _{SERCA}}{D_{Ca}V_{C}}\dfrac{C_{G}^{2}}{K_{SERCA}^{2}+C_{G}^{2}}\right] \Delta t\nonumber \\&\qquad +(1-\Psi )\left[ \frac{\lambda _{LK}}{D_{Ca}V_{C}}\left( \dfrac{C_{T}-V_{C}C_{G}^{0}}{V_{E}}-C_{G}^{0}\right) -\frac{\lambda _{SERCA}}{D_{Ca}V_{C}}\dfrac{(C_{G}^{0})^{2}}{K_{SERCA}^{2}+(C_{G}^{0})^{2}}\right] \Delta t, \end{aligned}$$

(29)

where the 0 super scripted values of C represents initial concentrations. The Crank Nicolson method is employed by substituting $\Psi = 1/2$. The hepatocyte cell is assumed to be discretized by 24 nodes. Equation (29) is arranged at ‘$j^{th}$’ iteration in the following form,

$$\begin{aligned} a_{G}C_{G}^{j}=a_{G}^{0}C_{G}^{j-1}+a_{E}[C_{E}^{j}+C_{E}^{j-1}]+a_{W}[C_{W}^{j}+C_{W}^{j-1}]+S_{u}+NLT_{G}^{j-1}, \end{aligned}$$

(30)

where,

$$\begin{aligned} a_{G}&=\left[ \frac{\delta x}{D_{Ca}\Delta t}+\frac{1}{2\delta x}+\frac{1}{2\delta x} +\frac{a}{2}\right] , \, a_{G}^{0}=\left[ \frac{\delta x}{D_{Ca}\Delta t}-\frac{1}{2\delta x}-\frac{1}{2\delta x} -\frac{a}{2}\right] \\ a_{E}& = a_{W}=\frac{1}{2\delta x} \, and \, S_{u}=a C_{{\infty }} \delta x, \end{aligned}$$

and nonlinear term of $Ca^{2+}$ is given by,

$$\begin{aligned}&NLT_{G}^{j}=\dfrac{\delta x}{2}. \frac{ \lambda _{IP3R}}{D_{Ca}V_{C}} \left( \dfrac{(P_{c})_{G}^{j-1}}{(P_{c})_{G}^{j-1}+K_{IP3}}\dfrac{C_{G}^{j-1}}{C_{G}^{j-1}+K_{Act}}\right) ^{3}. \\&\quad \left( \dfrac{K_{Inh}}{K_{Inh}+C_{G}^{j-1}}\right) ^{3}\left( \dfrac{C_{T}-V_{C}C_{G}^{j-1}}{V_{E}} -C_{G}^{j-1}\right) \\&\qquad + \dfrac{\delta x}{2}\left[ \frac{\lambda _{LK}}{D_{Ca}V_{C}}\left( \dfrac{C_{T}-V_{C}C_{G}^{j-1}}{V_{E}}-C_{G}^{j-1}\right) -\frac{\lambda _{SERCA}}{D_{Ca}V_{C}}\dfrac{(C_{G}^{j-1})^{2}}{K_{SERCA}^{2}+(C_{G}^{j-1})^{2}}\right] . \end{aligned}$$

First boundary condition can be incorporated by setting, $C_{W}=\sigma _{Ca}$ and $a_{W}=0$,

$$\begin{aligned} a_{G}C_{G}^{j}=a_{G}^{0}C_{G}^{j-1}+a_{E}[C_{E}^{j}+C_{E}^{j-1}]+S_{u}+NLT_{G}^{j-1}, \end{aligned}$$

(31)

where

$$\begin{aligned} a_{G}&=\left[ \frac{\delta x}{D_{Ca}\Delta t}+\frac{1}{2\delta x}+\left( \frac{1}{\delta x} +\frac{a}{2}\right) \right] , \, a_{G}^{0}=\left[ \frac{\delta x}{D_{Ca}\Delta t}-\frac{1}{2\delta x}-\left( \frac{1}{\delta x} +\frac{a}{2}\right) \right] , \\ a_{E}&=\frac{1}{2\delta x} \, and \, S_{u}=\dfrac{2 \sigma _{Ca}}{\delta x}+a C_{{\infty }} \delta x. \end{aligned}$$

Second boundary condition can be incorporated by setting $C_{\infty }=0.1 \,\mu M$ and $a_{E}=0$,

$$\begin{aligned} a_{G}C_{G}^{j}=a_{G}^{0}C_{G}^{j-1}+a_{W}[C_{W}^{j}+C_{W}^{j-1}]+S_{u}+NLT_{G}^{j}, \end{aligned}$$

(32)

where,

$$\begin{aligned} a_{G}&=\left[ \frac{\delta x}{D_{Ca}\Delta t}+\frac{1}{2\delta x}+\left( \frac{1}{\delta x} +\frac{a}{2}\right) \right] , \, a_{G}^{0}=\left[ \frac{\delta x}{D_{Ca}\Delta t}-\frac{1}{2\delta x}-\left( \frac{1}{\delta x} +\frac{a}{2}\right) \right] ,\nonumber \\ a_{E}&=\frac{1}{2\delta x} \, and \, S_{u}=\dfrac{2 C_{\infty }}{\delta x}+a C_{{\infty }} \delta x. \end{aligned}$$

Integrating Eq. (24) along spatial dimension we get,

$$\begin{aligned}\dfrac{\delta x}{D_{P}}\int ^{t+\Delta t}_{t}\frac{\partial (P_{c})_{G}}{\partial t} dt&=\int ^{t+\Delta t}_{t} \left( \frac{\partial P_{c}}{\partial x} \right) _{e}-\left( \frac{\partial P_{c}}{\partial x} \right) _{w} dt \nonumber \\&\qquad +\dfrac{V_{Prod}}{D_{P}V_{C}}\int ^{t+\Delta t}_{t} \left[ \dfrac{C_{G}^{2}}{C_{G}^{2}+K_{Prod}^{2}}\right] dt\nonumber \\&\qquad -\dfrac{\lambda \delta x}{D_{P}V_{C}}\int ^{t+\Delta t}_{t} \left( 1-\dfrac{C_{G}}{C_{G}+0.39} \right) V_{1} \dfrac{(P_{c})_{G}}{(P_{c})_{G}+2.5} \nonumber \\&\qquad +\dfrac{C_{G}}{C_{G}+0.39} V_{2}\dfrac{(P_{c})_{G}}{(P_{c})_{G}+0.5}+ V_{3}\dfrac{(P_{c})_{G}}{(P_{c})_{G}+30} dt. \end{aligned}$$

(33)

The time integral is simplified using the weighted parameter $\Psi$, where $\Psi \in \left[ 0, 1 \right]$.

$$\begin{aligned}&\dfrac{\delta x}{D_{P}} [(P_{c})_{G}-(P_{c})_{G}^{0}]= \Psi \left[ \frac{(P_{c})_{E}-(P_{c})_{G}}{\delta x} -\frac{(P_{c})_{G}-(P_{c})_{W}}{\delta x}\right] \Delta t \nonumber \\&\qquad +(1-\Psi ) \left[ \frac{(P_{c})_{E}^{0}-(P_{c})_{G}^{0}}{\delta x} -\frac{(P_{c})_{G}^{0}-(P_{c})_{W}^{0}}{\delta x}\right] \Delta t \nonumber \\&\qquad \delta x\Psi \dfrac{V_{Prod}}{D_{P}V_{C}}\left[ \dfrac{C_{G}^{2}}{C_{G}^{2}+K_{Prod}^{2}}\right] \Delta t+\delta x(1-\Psi )\dfrac{V_{Prod}}{D_{P}V_{C}}\left[ \dfrac{(C_{G}^{0})^{2}}{(C_{G}^{0})^{2}+K_{Prod}^{2}}\right] \Delta t \nonumber \\&\qquad -\dfrac{\lambda \Psi \delta x}{D_{P}V_{C}}\left( 1-\dfrac{C_{G}}{C_{G}+0.39} \right) V_{1} \dfrac{(P_{c})_{G}}{(P_{c})_{G}+2.5}+\dfrac{C_{G}}{C_{G}+0.39} V_{2}\dfrac{(P_{c})_{G}}{(P_{c})_{G}+0.5}+ V_{3}\dfrac{(P_{c})_{G}}{(P_{c})_{G}+30} . \Delta t \nonumber \\&\qquad -\dfrac{\lambda (1-\Psi )\delta x}{D_{P}V_{C}} \left( 1-\dfrac{C_{G}^{0}}{C_{G}^{0}+0.39} \right) V_{1} \dfrac{(P_{c})_{G}^{0}}{(P_{c})_{G}^{0}+2.5} \nonumber \\&\qquad +\dfrac{C_{G}^{0}}{C_{G}^{0}+0.39} V_{2}\dfrac{(P_{c})_{G}^{0}}{(P_{c})_{G}^{0}+0.5}+ V_{3}\dfrac{(P_{c})_{G}^{0}}{(P_{c})_{G}^{0}+30} . \Delta t, \end{aligned}$$

(34)

where the 0 super scripted values of P represents initial concentrations. The Crank Nicolson method is employed by substituting $\Psi = 1/2$. Equation (34) is arranged in the following form for all internal nodes at ‘$j^{th}$’ iteration,

$$\begin{aligned} b_{G}(P_{c})_{G}^{j}=b_{G}^{0}(P_{c})_{G}^{j-1}+b_{E}[(P_{c})_{E}^{j}+(P_{c})_{E}^{j-1}]+b_{W}[(P_{c})_{W}^{j}+(P_{c})_{W}^{j-1}]-NLTP_{G}^{j-1}, \end{aligned}$$

(35)

where,

$$\begin{aligned} b_{G}=\left[ \frac{\delta x}{D_{P}\Delta t}+\frac{1}{2\delta x}+\frac{1}{2\delta x}\right] , \, b_{G}^{0}=\left[ \frac{\delta x}{D_{P}\Delta t}-\frac{1}{2\delta x}-\frac{1}{2\delta x} \right] \, and \, b_{E}=b_{W}=\frac{1}{2\delta x}, \end{aligned}$$

and nonlinear term of $IP_{3}$ is given by,

$$\begin{aligned}NLTP_{G}^{j-1}&=\dfrac{\lambda \delta x}{D_{P}V_{C}}. \left( 1-\dfrac{C_{G}^{j-1}}{C_{G}^{j-1}+0.39} \right) V_{1} \dfrac{(P_{c})_{G}^{j-1}}{(P_{c})_{G}^{j-1}+2.5} \\&\qquad + \dfrac{C_{G}^{j-1}}{C_{G}^{j-1}+0.39} V_{2}\dfrac{(P_{c})_{G}^{j-1}}{(P_{c})_{G}^{j-1}+0.5}+ V_{3}\dfrac{(P_{c})_{G}^{j-1}}{(P_{c})_{G}^{j-1}+30} . \nonumber \end{aligned}$$

First boundary condition can be incorporated by setting, $(P_{c})_{E}=\sigma _{P}$ and $b_{E}=0$,

$$\begin{aligned} b_{G}(P_{c})_{G}^{j}=b_{G}^{0}(P_{c})_{G}^{j-1}+b_{W}[(P_{c})_{W}^{j}+(P_{c})_{W}^{j-1}]+S_{u}+NLTP_{G}^{j-1}, \end{aligned}$$

(36)

where

$$\begin{aligned} b_{G}=\left[ \frac{\delta x}{D_{P}\Delta t}+\frac{1}{2\delta x}+ \frac{1}{\delta x}\right] , \, b_{G}^{0}=\left[ \frac{\delta x}{D_{P}\Delta t}-\frac{1}{2\delta x}-\frac{1}{\delta x}\right] , \, b_{W}=\frac{1}{2\delta x} \, and \, S_{u}=\dfrac{2 \sigma _{P}}{\delta x}. \end{aligned}$$

Second boundary condition can be incorporated by setting $P_{\infty }=10 \mu M$ and $a_{W}=0$,

$$\begin{aligned} b_{G}(P_{c})_{G}^{j}=b_{G}^{0}(P_{c})_{G}^{j-1}+b_{E}[(P_{c})_{E}^{j}+(P_{c})_{E}^{j-1}]+S_{u}+NLTP_{G}^{j-1}, \end{aligned}$$

(37)

where

$$\begin{aligned} b_{G}=\left[ \frac{\delta x}{D_{P}\Delta t}+\frac{1}{2\delta x}+ \frac{1}{\delta x}\right] , \, b_{G}^{0}=\left[ \frac{\delta x}{D_{P}\Delta t}-\frac{1}{2\delta x}-\frac{1}{\delta x}\right] , \, b_{E}=\frac{1}{2\delta x} \, and \, S_{u}=\dfrac{2 P_{\infty }}{\delta x}. \end{aligned}$$

All discretized equations obtained from Eqs. (30)– (32) and Eqs. (35)– (37) are expressed in matrix form as follows;

$$\begin{aligned}{}[L]_{24\times 24}*\begin{bmatrix} C \\ P_{c} \end{bmatrix}_{24\times 1}=[M]_{24\times 1}, \end{aligned}$$

(38)

where [L] is diagonal block matrix, $\begin{bmatrix} C \\ P_{c}\end{bmatrix}$ is calcium and $IP_{3}$ concentration vector, [M] is constant vector. At each time step Eq. (38) is solved by using Gauss-Seidel’s method to get desired solution vector $\begin{bmatrix} C \\ P_{c} \end{bmatrix}_{24\times 1}$