Skip to main content
SpringerLink
Log in

Analytic solutions for (2+1)-dimensional shallow water equations with flat bottom through Lie symmetry approach

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

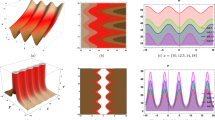
Two–dimensional optimal classification is performed for two–dimensional shallow water equations with flat bottom in Cartesian coordinates. In the proof of optimality of subalgebras, adjoint actions play a very vital role. When the nonidentical adjoint actions are more complicated then the situation becomes very challenging. Here, we propose a tree structure to handle such situations. Further, the optimal set is constructed with judicious adjoint actions. Consequently group invariant solutions are obtained and graphical behavior of solutions are demonstrated for some of the inequivalent classes in optimal system. Finally, physically relevant solutions like, traveling wave solutions, namely, the kink-type and peakon-type solitons, are obtained through traveling wave transformations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data Availibility Statement

This work does not contain any data to analyze.

References

  1. X.Y. Gao, Y. J. Guo, W.-R. Shan, Optical waves/modes in a multicomponent inhomogeneous optical fiber via a three-coupled variable-coefficient nonlinear schrödinger system. Appl. Math. Lett. 120, 107161 (2021)

    Article  MATH  Google Scholar 

  2. X.Y. Gao, Y.J. Guo, W.-R. Shan, In nOnlinear Optics, Fluid Mechanics, Plasma Physics Or Atmospheric Science: Symbolic Computation on A Generalized Variable-Coefficient Korteweg-de Vries Equation (Acta Mathematica Sinica, English Series, 2022), pp.1–9

    Google Scholar 

  3. D.Y. Yang, B. Tian, Q.X. Qu, C. R. Zhang, S.S. Chen, C. C. Wei, Lax pair, conservation laws, darboux transformation and localized waves of a variable-coefficient coupled hirota system in an inhomogeneous optical fiber. Chaos Solitons Fractals 150, 110487 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  4. S. Sil, T. Raja Sekhar, Nonlocally related systems, nonlocal symmetry reductions and exact solutions for one-dimensional macroscopic production model. Eur. Phys. J. Plus 135(6), 1–23 (2020)

    Article  Google Scholar 

  5. S.M. Sahoo, T. Raja Sekhar, G.P. Raja Sekhar, Exact solutions of generalized Riemann problem for nonhomogeneous shallow water equations. Indian J. Pure Appl. Math. 51(3), 1225–1237 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  6. X.-Y. Gao, Y.-J. Guo, W.-R. Shan, Looking at an open sea via a generalized (2+ 1)-dimensional dispersive long-wave system for the shallow water: scaling transformations, hetero-bäcklund transformations, bilinear forms and n solitons. Eur. Phys. J. Plus 136(8), 1–9 (2021)

    Article  Google Scholar 

  7. Q. Douglas, Felix Klein Sophus Lie, evolution of the idea of symmetry in the nineteenth century by IM Yaglom. Translated by Sergei Sossinsky and edited by Hardy grant and Abe Shenitzer pp 237. SFr68. 1988. ISBN 0-8176-3316-2 (Birkhäuser). Math. Gazette 72(462), 341–342 (1988)

    Article  Google Scholar 

  8. L.V. Ovsiannikov, Group Analysis of Differential Equations (Academic Press, Cambridge, 1982)

    MATH  Google Scholar 

  9. F. Galas, E.W. Richter, Exact similarity solutions of ideal MHD equations for plane motions. Phys. D 50(2), 297–307 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  10. P.J. Olver, Applications of Lie Groups to Differential Equations (Springer Science & Business Media, Heidelberg, 2000)

    MATH  Google Scholar 

  11. A. Bihlo, Symmetry methods in the atmospheric sciences. PhD thesis, uniwien, (2010)

  12. P. Satapathy, T. Raja Sekhar, D. Zeidan, Codimension two lie invariant solutions of the modified Khokhlov–Zabolotskaya–Kuznetsov equation. Math. Methods Appl. Sci. 44(6), 4938–4951 (2021)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. S. Özer, On the equivalence groups for (2+ 1) dimensional nonlinear diffusion equation. Nonlinear Anal. Real World Appl. 43, 155–166 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  14. B. Mayil Vaganan, T. Shanmuga Priya, Exact analytic, regular perturbation and numerical solutions of symmetry reductions of a (2+ 1)-dimensional kdv–burgers equation. Nonlinear Anal. Real World Appl. 14(3), 1265–1275 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  15. E. Demetriou, N.M. Ivanova, C. Sophocleous, Group analysis of (2+ 1)-and (3+ 1)-dimensional diffusion-convection equations. J. Math. Anal. Appl. 348(1), 55–65 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  16. A. Bihlo, R.O. Popovych, Lie symmetries and exact solutions of the barotropic vorticity equation. J. Math. Phys. 50(12), 123102 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. A. Bihlo, R.O. Popovych, Lie reduction and exact solutions of vorticity equation on rotating sphere. Phys. Lett. A 376(14), 1179–1184 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. W. Lai, A.A. Khan, A discontinuous galerkin method for two-dimensional shallow water flows. Int. J. Numer. Meth. Fluids 70(8), 939–960 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. A. Bihlo, R.O. Popovych, Invariant discretization schemes for the shallow-water equations. SIAM J. Sci. Comput. 34(6), B810–B839 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  20. X.-Y. Gao, Y.-J. Guo, W.-R. Shan, Bilinear forms through the binary bell polynomials, n solitons and bäcklund transformations of the Boussinesq-burgers system for the shallow water waves in a lake or near an ocean beach. Commun. Theor. Phys. 72(9), 095002 (2020)

    Article  ADS  MATH  Google Scholar 

  21. H. Yoshioka, K. Unami, M. Fujihara, A finite element/volume method model of the depth-averaged horizontally 2D shallow water equations. Int. J. Numer. Meth. Fluids 75(1), 23–41 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  22. Bobby Minola Ginting, A two-dimensional artificial viscosity technique for modelling discontinuity in shallow water flows. Appl. Math. Model. 45, 653–683 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  23. Y.A. Chirkunov, S.Y. Dobrokhotov, S.B. Medvedev, D.S. Minenkov, Exact solutions of one-dimensional nonlinear shallow water equations over even and sloping bottoms. Theor. Math. Phys. 178(3), 278–298 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  24. T. Raja Sekhar, V.D. Sharma, Similarity analysis of modified shallow water equations and evolution of weak waves. Commun. Nonlinear Sci. Numer. Simul. 17(2), 630–636 (2012)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. S. Szatmari, A. Bihlo, Symmetry analysis of a system of modified shallow-water equations. Commun. Nonlinear Sci. Numer. Simul. 19(3), 530–537 (2014)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  26. A.A. Chesnokov, Symmetries of shallow water equations on a rotating plane. J. Appl. Ind. Math. 4(1), 24–34 (2010)

    Article  MathSciNet  Google Scholar 

  27. A. Bihlo, R.O. Popovych, Invariant discretization schemes for the shallow-water equations. SIAM J. Sci. Comput. 34(6), B810–B839 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  28. Alexander. Bihlo, Nataliia. Poltavets, and R O. Popovych, Lie symmetries of two-dimensional shallow water equations with variable bottom topography. arxiv:1911.02097 (2019)

  29. M. Wang, B. Tian, H. Cong-Cong, S.-H. Liu, Generalized darboux transformation, solitonic interactions and bound states for a coupled fourth-order nonlinear schrödinger system in a birefringent optical fiber. Appl. Math. Lett. 119, 106936 (2021)

    Article  MATH  Google Scholar 

  30. X.-T. Gao, B. Tian, Y. Shen, C.-H. Feng, Comment on “shallow water in an open sea or a wide channel: auto-and non-auto-bäcklund transformations with solitons for a generalized (2+ 1)-dimensional dispersive long-wave system’’. Chaos Solitons Fractals 151, 111222 (2021)

    Article  MATH  Google Scholar 

  31. Y. Shen, B. Tian, Bilinear auto-bäcklund transformations and soliton solutions of a (3+ 1)-dimensional generalized nonlinear evolution equation for the shallow water waves. Appl. Math. Lett. 122, 107301 (2021)

    Article  MATH  Google Scholar 

  32. A.R. Seadawy, M. Iqbal, D. Lu, Applications of propagation of long-wave with dissipation and dispersion in nonlinear media via solitary wave solutions of generalized kadomtsev–petviashvili modified equal width dynamical equation. Comput. Math. Appl. 78(11), 3620–3632 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  33. G.W. Bluman, S. Anco, Symmetry and integration methods for differential equations (Springer Science & Business Media, New York, 2008)

    MATH  Google Scholar 

Download references

Acknowledgements

We sincerely thank the anonymous referees for their useful comments and suggestions to improve the manuscript. Research support from, DST/ INSPIRE Fellowship/2013, Ministry of Science and Technology, Department of Science and Technology, Government of India and Sponsored Research and Industrial Consultancy, IIT Kharagpur (Ref no. IIT/SRIC/ISIRD/2013–14) are gratefully acknowledged by first and second authors, respectively.

Author information

Authors and Affiliations

  1. Department of Mathematics, Visvesvaraya National Institute of Technology Nagpur, Nagpur, India

    Purnima Satapathy

  2. Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur 2, India

    T. Raja Sekhar

Authors
  1. Purnima Satapathy
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Raja Sekhar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Raja Sekhar.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Satapathy, P., Raja Sekhar, T. Analytic solutions for (2+1)-dimensional shallow water equations with flat bottom through Lie symmetry approach. Eur. Phys. J. Plus 137, 1183 (2022). https://doi.org/10.1140/epjp/s13360-022-03373-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-022-03373-4

Search

Navigation