Abstract
Calcium ([Ca2+]), IP3, and nitric oxide (NO) play a significant role in cell signaling to maintain various physiological functions. Calcium and IP3 regulation has been investigated independently in a variety of cells like myocyte, hepatocyte, and neuron cells. However, very little attention has been paid to the study of interdependent calcium and IP3 dynamics regulating nitric oxide production in neurons and other cells. Nitric oxide and its derivatives are reported to be involved in the pathogenic process leading to neurogenerative disorders like Parkinson’s disease. The production of nitric oxide depends on the calcium dynamics in a neuron cell. Therefore a model is proposed to study the regulatory and dysregulatory effects of interdependent calcium and IP3 dynamics in a neuron cell. The system of reaction–diffusion equations for calcium and IP3 is coupled with the production of nitric oxide in a neuron cell to formulate an initial boundary value problem. The finite element simulation is performed to obtain results for regulatory and dysregulatory conditions of interdependent calcium and IP3 dynamics along with nitric oxide production in the cell. It is observed that disorders in mechanisms of calcium dynamics are balanced to some extent by IP3 dynamics. The dysregulation of calcium or IP3 dynamics causes an increase or decrease in nitric oxide production in the cell, which can lead to various neurodegenerative disorders. The information obtained from the present study can be used in the development of diagnostic and therapeutic measures.




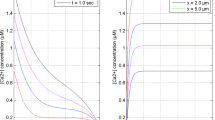
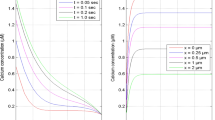
source influx (σ) at t = 1.0 s and x = 0 μm for [B] = 5 μM











Similar content being viewed by others
Data availability
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
References
J. Crank, The mathematics of diffusion (Oxford University Press, 1979)
R. Llinas, The role of calcium in neuronal function. Neurosci. Fourth Study Progr. 65, 555–571 (1979)
A.L. Fogelson, R.S. Zucker, Presynaptic calcium diffusion from various arrays of single channels. Implications for transmitter release and synaptic facilitation. Biophys. J. 48, 1003–1017 (1985). https://doi.org/10.1016/S0006-3495(85)83863-7
Z. Ahmed, J.A. Connor, Calcium regulation by and buffer capacity of molluscan neurons during calcium transients. Cell Calcium 9, 57–69 (1988). https://doi.org/10.1016/0143-4160(88)90025-5
M.D. Bootman, M.J. Berridge, The elemental principles of calcium signaling. Cell 83, 675–678 (1995). https://doi.org/10.1016/0092-8674(95)90179-5
J. Wagner, J. Keizer, Effects of rapid buffers on Ca2+ diffusion and Ca2+ oscillations. Biophys. J. 67, 447–456 (1994). https://doi.org/10.1016/S0006-3495(94)80500-4
G.D. Smith, Analytical steady-state solution to the rapid buffering approximation near an open Ca2+ channel. Biophys. J. 71, 3064–3072 (1996). https://doi.org/10.1016/S0006-3495(96)79500-0
G.D. Smith, J. Wagner, J. Keizer, Validity of the rapid buffering approximation near a point source of calcium ions. Biophys. J. 70, 2527–2539 (1996). https://doi.org/10.1016/S0006-3495(96)79824-7
D.M. Egelman, P.R. Montague, Calcium dynamics in the extracellular space of mammalian neural tissue. Biophys. J. 76, 1856–1867 (1999). https://doi.org/10.1016/S0006-3495(99)77345-5
A. Verkhratsky, The endoplasmic reticulum and neuronal calcium signalling. Cell Calcium 32, 393–404 (2002). https://doi.org/10.1016/S0143416002001896
M. Falcke, Buffers and oscillations in intracellular Ca2+ dynamics. Biophys. J. 84, 28–41 (2003). https://doi.org/10.1016/S0006-3495(03)74830-9
D.D. Dave, B.K. Jha, Mathematical modeling of calcium oscillatory patterns in a neuron,. Interdiscip. Sci. Comput Life Sci. 13, 12–24 (2021). https://doi.org/10.1007/s12539-020-00401-8
J. Sneyd, K. Tsaneva-Atanasova, J.I.E. Bruce, S.V. Straub, D.R. Giovannucci, D.I. Yule, A model of calcium waves in pancreatic and parotid acinar cells. Biophys. J. 85, 1392–1405 (2003). https://doi.org/10.1016/S0006-3495(03)74572-X
M. Brini, T. Calì, D. Ottolini, E. Carafoli, Neuronal calcium signaling: function and dysfunction. Cell. Mol. Life Sci. 71, 2787–2814 (2014). https://doi.org/10.1007/s00018-013-1550-7
A. Jha, N. Adlakha, Analytical solution of two dimensional unsteady state problem of calcium diffusion in a neuron cell. J. Med. Imaging Heal. Informatics. 4, 547–553 (2014). https://doi.org/10.1166/jmihi.2014.1282
B.K. Jha, N. Adlakha, M.N. Mehta, Two-dimensional finite element model to study calcium distribution in astrocytes in presence of VGCC and excess buffer. Int. J. Model. Simulation. Sci. Comput. 4, 681 (2013). https://doi.org/10.1142/S1793962312500304
A. Tripathi, N. Adlakha, Closed form solution to problem of calcium diffusion in cylindrical shaped neuron cell. World Acad. Sci Eng. Technol. 80, 739–742 (2011)
A. Tripathi, N. Adlakha, Two dimensional coaxial circular elements in FEM to study calcium diffusion in neuron cells. Appl. Math. Sci. 6, 455–466 (2012)
V. Tewari, S. Tewari, K.R. Pardasani, A model to study the effect of excess buffers and Na + ions on Ca 2+ diffusion in neuron cell,. World Acad. Sci Eng. Technol. 76, 41–46 (2011). https://doi.org/10.5281/zenodo.1054988
A. Jha, N. Adlakha, Two-dimensional finite element model to study unsteady state Ca2+ diffusion in neuron involving ER LEAK and SERCA. Int. J. Biomath. 8, 80 (2015). https://doi.org/10.1142/S1793524515500023
S.G. Tewari, K.R. Pardasani, Finite element model to study two dimensional unsteady state cytosolic calcium diffusion in presence of excess buffers. IAENG Int. J. Appl. Math. 40, 1–5 (2010)
S. Tewari, K.R. Pardasani, Finite difference model to study the effects of Na + influx on cytosolic Ca 2 + diffusion. World Acad. Sci. Eng. Technol. 63, 670–675 (2008)
N. Manhas, J. Sneyd, K.R. Pardasani, Modelling the transition from simple to complex Ca2+oscillations in pancreatic acinar cells. J. Biosci. 39, 463–484 (2014). https://doi.org/10.1007/s12038-014-9430-3
N. Manhas, K.R. Pardasani, Mathematical model to study IP3 Dynamics dependent calcium oscillations in pancreatic acinar cells. J. Med. Imag. Heal. Informatics. 4, 874–880 (2014). https://doi.org/10.1166/jmihi.2014.1333
K.B. Pathak, N. Adlakha, Finite element model to study calcium signalling in cardiac myocytes involving pump, leak and excess buffer. J. Med. Imag. Heal. Informatics. 5, 683–688 (2015). https://doi.org/10.1166/jmihi.2015.1443
K. Pathak, N. Adlakha, Finite element model to study two dimensional unsteady state calcium distribution in cardiac myocytes, Alexandria. J. Med. 52, 261–268 (2016). https://doi.org/10.1016/j.ajme.2015.09.007
P.A. Naik, K.R. Pardasani, One dimensional finite element model to study calcium distribution in oocytes in presence of VGCC, RyR and buffers. J. Med. Imag. Heal. Informatics. 5, 471–476 (2015). https://doi.org/10.1166/jmihi.2015.1431
P.A. Naik, K.R. Pardasani, Three-dimensional finite element model to study effect of RyR calcium channel, ER leak and SERCA pump on calcium distribution in oocyte cell. Int. J. Comput. Methods. 16, 1–19 (2019). https://doi.org/10.1142/S0219876218500913
P.A. Naik, K.R. Pardasani, Finite element model to study calcium distribution in oocytes involving voltage gated Ca 2+ channel, ryanodine receptor and buffers,. Alexandria J. Med. 52, 43–49 (2016). https://doi.org/10.1016/j.ajme.2015.02.002
S. Panday, K.R. Pardasani, Finite element model to study effect of advection diffusion and Na +/Ca2+ exchanger on Ca2+ distribution in oocytes. J. Med. Imag. Heal. Informatics. 3, 374–379 (2013). https://doi.org/10.1166/jmihi.2013.1184
M. Kotwani, N. Adlakha, M.N. Mehta, Numerical model to study calcium diffusion in fibroblasts cell for one dimensional unsteady state case. Appl. Math. Sci. 6, 5063–5072 (2012)
M. Kotwani, N. Adlakha, M.N. Mehta, Finite element model to study the effect of buffers, source amplitude and source geometry on spatiooral calcium distribution in fibroblast cell. J. Med. Imag. Heal. Informatics. 4, 840–847 (2014). https://doi.org/10.1166/jmihi.2014.1328
Y.D. Jagtap, N. Adlakha, Simulation of buffered advection diffusion of calcium in a hepatocyte cell. Math. Biol. Bioinforma. 13, 609–619 (2018). https://doi.org/10.17537/2018.13.609
S.G. Tewari, K.R. Pardasani, Modeling effect of sodium pump on calcium oscillations in neuron cells. J. Multiscale Model. 04, 1250010 (2012). https://doi.org/10.1142/s1756973712500102
B.K. Jha, N. Adlakha, M.N. Mehta, Two-dimensional finite element model to study calcium distribution in astrocytes in presence of excess buffer. Int. J. Biomath. 7, 1–11 (2014). https://doi.org/10.1142/S1793524514500314
D.D. Dave, B.K. Jha, 3D mathematical modeling of calcium signaling in Alzheimer’s disease. Netw. Model. Anal. Heal. Informatics Bioinforma. 9, 1–10 (2020). https://doi.org/10.1007/s13721-019-0207-3
D.D. Dave, B.K. Jha, 2D finite element estimation of calcium diffusion in Alzheimer’s affected neuron. Netw. Model. Anal. Heal. Informatics Bioinforma. 10, 1–11 (2021). https://doi.org/10.1007/s13721-021-00322-6
H. Joshi, B.K. Jha, On a reaction–diffusion model for calcium dynamics in neurons with Mittag-Leffler memory. Eur. Phys. J. Plus. 136, 12 (2021). https://doi.org/10.1140/epjp/s13360-021-01610-w
B.K. Jha, H. Joshi, Chaos of calcium diffusion in Parkinson s infectious disease model and treatment mechanism via Hilfer fractional derivative. Math. Model. Numer. Simul. with Appl. 1, 84–94 (2021). https://doi.org/10.53391/mmnsa.2021.01.008
M.J. Berridge, P. Lipp, M.D. Bootman, The versatility and universality of calcium signalling. Nat. Rev. Mol. Cell Biol. 2000(11), 11–21 (2000). https://doi.org/10.1038/35036035
R.H. Michell, Inositol phospholipids and cell surface receptor function. BBA - Rev. Biomembr. 415, 81–147 (1975). https://doi.org/10.1016/0304-4157(75)90017-9
M.J. Berridge, R.F. Irvine, Inositol trisphosphate, a novel second messenger in cellular signal transduction. Nature 312, 315–321 (1984). https://doi.org/10.1038/312315a0
I. Bezprozvanny, J. Watras, B.E. Ehrlich, Bell-shaped calcium-response curves of lns(l,4,5)P3- and calcium-gated channels from endoplasmic reticulum of cerebellum. Nature 351, 751–754 (1991). https://doi.org/10.1038/351751a0
C.E. Sims, N.L. Allbrittont, Metabolism of inositol 1,4,5-trisphosphate and inositol 1,3,4,5- tetrakisphosphate by the oocytes of Xenopus laevis. J. Biol. Chem. 273, 4052–4058 (1998). https://doi.org/10.1074/jbc.273.7.4052
J. Keizer, G. De Young, Effect of voltage-gated plasma membrane Ca2+ fluxes on IP3-linked Ca2+ oscillations. Cell Calcium 14, 397–410 (1993). https://doi.org/10.1016/0143-4160(93)90044-7
Y.X. Li, J. Rinzel, Equations for InsP3 receptor-mediated [Ca2+](i) oscillations derived from a detailed kinetic model: A hodgkin-huxley like formalism. J. Theor. Biol. 166, 461–473 (1994). https://doi.org/10.1006/jtbi.1994.1041
M. Falcke, R. Huerta, M.I. Rabinovich, H.D.I. Abarbanel, R.C. Elson, A.I. Selverston, Modeling observed chaotic oscillations in bursting neurons: The role of calcium dynamics and IP3. Biol. Cybern. 82, 517–527 (2000). https://doi.org/10.1007/s004220050604
J. Wagner, C.F. Fall, F. Hong, C.E. Sims, N.L. Allbritton, R.A. Fontanilla, I.I. Moraru, L.M. Loew, R. Nuccitelli, A wave of IP3 production accompanies the fertilization Ca2+ wave in the egg of the frog, Xenopus laevis: Theoretical and experimental support. Cell Calcium 35, 433–447 (2004). https://doi.org/10.1016/j.ceca.2003.10.009
J. Garthwaite, Glutamate, nitric oxide and cell-cell signalling in the nervous system. Trends Neurosci. 14, 60–67 (1991). https://doi.org/10.1016/0166-2236(91)90022-M
M. Salter, G. Knowles, Activity of -Dependent and -Independent Nitric Oxide S. FEBS Lett. 291, 145–149 (1991)
G. Garthwaite, J. Garthwaite, Cyclic GMP and cell death in rat cerebellar slices. Neuroscience 26, 321–326 (1988). https://doi.org/10.1016/0306-4522(88)90148-0
J. Wood, J. Garthwaite, Models of the diffusional spread of nitric oxide: Implications for neural nitric oxide signalling and its pharmacological properties. Neuropharmacology 33, 1235–1244 (1994). https://doi.org/10.1016/0028-3908(94)90022-1
H. Van Liew, S. Raychaudhuri, Modeling in physiology. J. Appl. Physiol. 82, 2045–2053 (1997)
N.M. Tsoukias, Nitric oxide bioavailability in the microcirculation: Insights from mathematical models. Microcirculation 15, 813–834 (2008). https://doi.org/10.1080/10739680802010070
S.R. Vincent, Nitric oxide neurons and neurotransmission. Prog. Neurobiol. 90, 246–255 (2010). https://doi.org/10.1016/j.pneurobio.2009.10.007
K.A. Kohlmeier, C.S. Leonard, Transmitter modulation of spike-evoked calcium transients in arousal related neurons: muscarinic inhibition of SNX-482-sensitive calcium influx. Eur. J. Neurosci. 23, 1151–1162 (2006). https://doi.org/10.1111/j.1460-9568.2006.04640.x
V.M. Bolotina, S. Najibi, J.J. Palacino, P.J. Pagano, R.A. Cohen, Nitric oxide directly activates calcium-dependent potassium channels in vascular smooth muscle. Nature 368, 850–853 (1994). https://doi.org/10.1038/368850a0
M. Kourosh-Arami, N. Hosseini, M. Mohsenzadegan, A. Komaki, M.T. Joghataei, Neurophysiologic implications of neuronal nitric oxide synthase. Rev. Neurosci. 31, 617–636 (2020). https://doi.org/10.1515/revneuro-2019-0111
M. Iino, Ca2+-dependent inositol 1,4,5-trisphosphate and nitric oxide signaling in cerebellar neurons. J. Pharmacol. Sci. 100, 538–544 (2006). https://doi.org/10.1254/jphs.CPJ06006X
W.G.G.Ã.L. Farnell, M.R. Bennett, A computational model relating changes in cerebral blood volume to synaptic activity in neurons. Neurocomputing 70, 1674–1679 (2007). https://doi.org/10.1016/j.neucom.2006.10.071
K. Dormanns, R.G. Brown, T. David, The role of nitric oxide in neurovascular coupling. J. Theor. Biol. 394, 1–17 (2016). https://doi.org/10.1016/j.jtbi.2016.01.009
N. Singh, N. Adlakha, Nonlinear dynamic modeling of 2-dimensional interdependent calcium and inositol 1,4,5-trisphosphate in cardiac myocyte. Math. Biol. Bioinforma. 14, 290–305 (2019). https://doi.org/10.17537/2019.14.290
N. Singh, N. Adlakha, Effect of source geometry on interdependent calcium and inositol 1; 4; 5-trisphosphate dynamics in a cardiac myocyte cell, Springer Proc. Math. Stat. 308, 75–83 (2020). https://doi.org/10.1007/978-981-15-1338-1_6
N. Singh, N. Adlakha, A mathematical model for interdependent calcium and inositol 1,4,5-trisphosphate in cardiac myocyte. Netw. Model. Anal. Heal. Informatics Bioinforma. 8, 253 (2019). https://doi.org/10.1007/s13721-019-0198-0
Y. Jagtap, N. Adlakha, Numerical study of one-dimensional buffered advection–diffusion of calcium and IP 3 in a hepatocyte cell. Netw. Model. Anal. Heal. Informatics Bioinforma. 8, 1–9 (2019). https://doi.org/10.1007/s13721-019-0205-5
A. Bugrim, R. Fontanilla, B.B. Eutenier, J. Keizer, R. Nuccitelli, Sperm initiate a Ca2+ wave in frog eggs that is more similar to Ca2+ waves initiated by IP3 than by Ca2+. Biophys. J. 84, 1580–1590 (2003). https://doi.org/10.1016/S0006-3495(03)74968-6
G. Dupont, S. Swillens, C. Clair, T. Tordjmann, L. Combettes, Hierarchical organization of calcium signals in hepatocytes: From experiments to models. Biochim. Biophys. Acta - Mol. Cell Res. 1498, 134–152 (2000). https://doi.org/10.1016/S0167-4889(00)00090-2
S.A. Brown, F. Morgan, J. Watras, L.M. Loew, Analysis of phosphatidylinositol-4,5-bisphosphate signaling in cerebellar Purkinje spines. Biophys. J. 95, 1795–1812 (2008). https://doi.org/10.1529/biophysj.108.130195
T. Öziş, E.N. Aksan, A. Özdeş, A finite element approach for solution of Burgers’ equation. Appl. Math. Comput. 139, 417–428 (2003). https://doi.org/10.1016/S0096-3003(02)00204-7
L. Zhang, V.L. Dawson, T.M. Dawson, Role of nitric oxide in Parkinson’s disease. Pharmacol. Ther. 109, 33–41 (2006). https://doi.org/10.1016/j.pharmthera.2005.05.007
Author information
Authors and Affiliations
Corresponding author
Appendix: summary of the model equations
Appendix: summary of the model equations
The shape function of calcium and IP3 concentration for each element is taken as,
Putting nodal conditions in Eq. 21, we obtain
where
By the Eq. 23, we have
And
Putting \({\text{q}}^{{\text{(e)}}}\) and \({\text{r}}^{{\text{(e)}}}\) from Eq. 25 in 21, we obtain
Discretized form of Eq. 1 and 7 is given by,
The integral \({\text{I}}_{{1}}^{{\text{(e)}}}\) and \({\text{I}}_{{2}}^{{\text{(e)}}}\) can be expressed in this formation
where
The various parameters \( \alpha ,\beta _{1} ,\gamma ,\kappa ,\eta ,\mu ,\tau ,\delta ,\xi ,{\text{and}},\omega \) are obtained by the linearization of nonlinear interdependent calcium and IP3 dynamics. The equations are analyzed and boundary conditions are included to give the following system of equations.
where
Here, the system matrices are A and B with the system vectors F. The Crank–Nicolson method which is numerically stable is applied to solve the time derivate in FEM.
Rights and permissions
About this article
Cite this article
Pawar, A., Raj Pardasani, K. Effects of disorders in interdependent calcium and IP3 dynamics on nitric oxide production in a neuron cell. Eur. Phys. J. Plus 137, 543 (2022). https://doi.org/10.1140/epjp/s13360-022-02743-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjp/s13360-022-02743-2