Skip to main content
SpringerLink
Log in

Theoretical analysis of thermoelastic damping of silver nanobeam resonators based on Green–Naghdi via nonlocal elasticity with surface energy effects

  • Regular Article
  • Published:
The European Physical Journal Plus Aims and scope Submit manuscript

Abstract

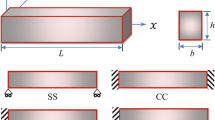
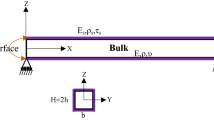
The vibration of a silver nanobeam resonator, considering the surface effect as well as the thermal effect has been investigated in this paper. The emerged bending in nanobeam resonator causes the surface effects to appear in nanobeam. The governing equations for nanobeam are obtained considering the surface and thermal effects and using the nonlocal elasticity theory. The temperature effects based on the Green–Naghdi thermoelasticity theory, and considering the thermoelastic damping, are taken into account. The vibration governing equations are derived by the coupled Green–Naghdi thermoelastic, nonlocal elasticity theory, and surface effect for Euler–Bernoulli beam model. The dynamic and temperature responses of the nanobeam are obtained in the Laplace domain using the Laplace method. The technique of inverse Laplace, called a Talbot method, is utilized to calculate the dynamic and thermal responses of the nanobeam in the time domain. To investigate the results, the effects of the various parameters, such as the surface effects, nonlocal parameter, and the initial temperature conditions, on the dynamic and temperature responses of the microbeam are scrutinized.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. A.W. McFarland, J.S. Colton, Role of material microstructure in plate stiffness with relevance to microcantilever sensors. J. Micromech. Microeng. 15(5), 1060 (2005)

    ADS  Google Scholar 

  2. R. de Souza Pereira, Atomic force microscopy as a novel pharmacological tool. Biochem. Pharmacol. 62(8), 975–983 (2001)

    Google Scholar 

  3. X. Li et al., Mechanical characterization of micro/nanoscale structures for MEMS/NEMS applications using nanoindentation techniques. Ultramicroscopy 97(1), 481–494 (2003)

    Google Scholar 

  4. J. Pei, F. Tian, T. Thundat, Glucose biosensor based on the microcantilever. Anal. Chem. 76(2), 292–297 (2004)

    Google Scholar 

  5. O. Rahmani et al., Torsional vibration of cracked nanobeam based on nonlocal stress theory with various boundary conditions: an analytical study. Int. J. Appl. Mech. 7(3), 1550036 (2015)

    Google Scholar 

  6. Z. Misagh, H. Seyed Amirhosein, A semi analytical method for electro-thermo-mechanical nonlinear vibration analysis of nanobeam resting on the Winkler-Pasternak foundations with general elastic boundary conditions. Smart Mater. Struct. 25(8), 085005 (2016)

    Google Scholar 

  7. M. Zarepour, S.A. Hosseini, M. Ghadiri, Free vibration investigation of nano mass sensor using differential transformation method. Appl. Phys. A 123(3), 181 (2017)

    ADS  Google Scholar 

  8. M. Namvar et al., Experimental and analytical investigations of vibrational behavior of U-shaped atomic force microscope probe considering thermal loading and the modified couple stress theory. Eur. Phys. J. Plus 132(6), 247 (2017)

    Google Scholar 

  9. B. Wiley, Y. Sun, Y. Xia, Polyol synthesis of silver nanostructures: control of product morphology with Fe(II) or Fe(III) species. Langmuir 21(18), 8077–8080 (2005)

    Google Scholar 

  10. B.J. Wiley et al., Synthesis and electrical characterization of silver nanobeams. Nano Lett. 6(10), 2273–2278 (2006)

    ADS  Google Scholar 

  11. M. Karimi, H.A. Haddad, A.R. Shahidi, Combining surface effects and non-local two variable refined plate theories on the shear/biaxial buckling and vibration of silver nanoplates. Micro Nano Lett. 10(6), 276–281 (2015)

    Google Scholar 

  12. A. Shahidi, Finite difference method for biaxial and uniaxial buckling of rectangular silver nanoplates resting on elastic foundations in thermal environments based on surface stress and nonlocal elasticity theories. J. Solid Mech. 8(4), 719–733 (2016)

    Google Scholar 

  13. H.M. Numanoğlu, Ö. Civalek, Elastic beam model and bending analysis of silver nanowires. Int. J. Eng. Appl. Sci. 10(1), 13–20 (2018)

    Google Scholar 

  14. A.C. Eringen, On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 54(9), 4703–4710 (1983)

    ADS  Google Scholar 

  15. A.C. Eringen, Nonlocal polar elastic continua. Int. J. Eng. Sci. 10(1), 1–16 (1972)

    MathSciNet  MATH  Google Scholar 

  16. A.C. Eringen, D. Edelen, On nonlocal elasticity. Int. J. Eng. Sci. 10(3), 233–248 (1972)

    MathSciNet  MATH  Google Scholar 

  17. H. Niknam, M. Aghdam, A semi analytical approach for large amplitude free vibration and buckling of nonlocal FG beams resting on elastic foundation. Compos. Struct. 119, 452–462 (2015)

    Google Scholar 

  18. M. Eltaher, A.E. Alshorbagy, F. Mahmoud, Vibration analysis of Euler-Bernoulli nanobeams by using finite element method. Appl. Math. Model. 37(7), 4787–4797 (2013)

    MathSciNet  MATH  Google Scholar 

  19. P. Soltani et al., Vibration of wavy single-walled carbon nanotubes based on nonlocal Euler Bernoulli and Timoshenko models. Int. J. Adv. Struct. Eng. (IJASE) 4(1), 1–10 (2012)

    Google Scholar 

  20. O. Rahmani, S.S. Asemani, S.A.H. Hosseini, Study the surface effect on the buckling of nanowires embedded in Winkler-Pasternak elastic medium based on a nonlocal. Theory. J. Nanostruct. 6(1), 87–92 (2016)

    Google Scholar 

  21. L. Wang, Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Phys. E 43(1), 437–439 (2010)

    Google Scholar 

  22. Z. Yan, L. Jiang, Vibration and buckling analysis of a piezoelectric nanoplate considering surface effects and in-plane constraints. Proc. R. Soc. A Math. Phys. Eng. Sci. 468(2147), 3458–3475 (2012)

    ADS  MathSciNet  MATH  Google Scholar 

  23. H.-L. Lee, W.-J. Chang, Surface and small-scale effects on vibration analysis of a nonuniform nanocantilever beam. Phys. E 43(1), 466–469 (2010)

    Google Scholar 

  24. B. Gheshlaghi, S.M. Hasheminejad, Vibration analysis of piezoelectric nanowires with surface and small scale effects. Curr. Appl. Phys. 12(4), 1096–1099 (2012)

    ADS  Google Scholar 

  25. R. Ansari, S. Sahmani, Surface stress effects on the free vibration behavior of nanoplates. Int. J. Eng. Sci. 49(11), 1204–1215 (2011)

    MathSciNet  MATH  Google Scholar 

  26. M. Zarepour, S. Hosseini, A. Akbarzadeh, Geometrically nonlinear analysis of Timoshenko piezoelectric nanobeams with flexoelectricity effect based on Eringen’s differential model. Appl. Math. Model. 69, 563–582 (2019)

    MathSciNet  Google Scholar 

  27. A.H. Hosseini et al., Axial vibration of cracked nanorods embedded in elastic foundation based on a nonlocal elasticity model. Sensor Lett. 14(10), 1019–1025 (2016)

    Google Scholar 

  28. A.E. Green, N. Laws, P. Naghdi, On the theory of water waves. Proc. R. Soc. Lond. A Math. Phys. Sci. 338(1612), 43–55 (1974)

    ADS  MathSciNet  MATH  Google Scholar 

  29. R. Ertekin, W. Webster, J. Wehausen, Waves caused by a moving disturbance in a shallow channel of finite width. J. Fluid Mech. 169, 275–292 (1986)

    ADS  MATH  Google Scholar 

  30. Webster, W. C., Kim, D. Y., The dispersion of large-amplitude gravity waves in deep water, in Proceedings of 18th Symposium On Naval Hydrodynamics, pp. 397–415 (1990)

  31. Q. Xu, J. Pawlowski, R. Baddour, Development of Green-Naghdi models with a wave-absorbing beach for nonlinear, irregular wave propagation. J. Mar. Sci. Technol. 2(1), 21–34 (1997)

    Google Scholar 

  32. Z. Demirbilek, W.C. Webster, The Green-Naghdi theory of fluid sheets for shallow-water waves, in Developments in Offshore Engineering (Elsevier, Berlin, 1999). p. 1–54

  33. A. Green, P. Naghdi, On undamped heat waves in an elastic solid. J. Therm. Stresses 15(2), 253–264 (1992)

    ADS  MathSciNet  Google Scholar 

  34. A. Green, P. Naghdi, Thermoelasticity without energy dissipation. J. Elast. 31(3), 189–208 (1993)

    MathSciNet  MATH  Google Scholar 

  35. M.I. Othman, M. Marin, Effect of thermal loading due to laser pulse on thermoelastic porous medium under GN theory. Results Phys. 7, 3863–3872 (2017)

    ADS  Google Scholar 

  36. M. Marin, E. Craciun, Uniqueness results for a boundary value problem in dipolar thermoelasticity to model composite materials. Compos. B Eng. 126, 27–37 (2017)

    Google Scholar 

  37. M. Hassan et al., Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids. Heat Transfer Res. 49, 18 (2018)

    Google Scholar 

  38. R. Barretta et al., Stress-driven nonlocal integral model for Timoshenko elastic nano-beams. Eur. J. Mech. A/Solids 72, 275–286 (2018)

    ADS  MathSciNet  MATH  Google Scholar 

  39. G. Romano, R. Barretta, Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B 114, 184–188 (2017)

    Google Scholar 

  40. R. Barretta et al., Stress-driven modeling of nonlocal thermoelastic behavior of nanobeams. Int. J. Eng. Sci. 126, 53–67 (2018)

    MathSciNet  MATH  Google Scholar 

  41. A. Apuzzo et al., Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model. Compos. B Eng. 123, 105–111 (2017)

    Google Scholar 

  42. A.M. Zenkour, A.E. Abouelregal, Vibration of FG nanobeams induced by sinusoidal pulse-heating via a nonlocal thermoelastic model. Acta Mech. 225(12), 3409–3421 (2014)

    MathSciNet  MATH  Google Scholar 

  43. S.M. Hosseini, Analytical solution for nonlocal coupled thermoelasticity analysis in a heat-affected MEMS/NEMS beam resonator based on Green-Naghdi theory. Appl. Math. Model. 57, 21–36 (2018)

    MathSciNet  MATH  Google Scholar 

  44. A.M. Zenkour, Nonlocal thermoelasticity theory without energy dissipation for nano-machined beam resonators subjected to various boundary conditions. Microsyst. Technol. 23(1), 55–65 (2017)

    Google Scholar 

  45. M. Rezazadeh, M. Tahani, S.M. Hosseini, Thermoelastic damping in a nonlocal nano-beam resonator as NEMS based on the type III of Green-Naghdi theory (with energy dissipation). Int. J. Mech. Sci. 92, 304–311 (2015)

    Google Scholar 

  46. S.M. Hosseini, Shock-induced nonlocal coupled thermoelasticity analysis (with energy dissipation) in a MEMS/NEMS beam resonator based on Green-Naghdi theory: A meshless implementation considering small-scale effects. J. Therm. Stresses 40(9), 1134–1151 (2017)

    Google Scholar 

  47. J.W. Gibbs, The Scientific Papers of J. Willard Gibbs (Longmans, Green and Company, Harlow, 1906)

    MATH  Google Scholar 

  48. R.C. Cammarata, Surface and interface stress effects in thin films. Prog. Surf. Sci. 46(1), 1–38 (1994)

    ADS  Google Scholar 

  49. G. Jing et al., Surface effects on elastic properties of silver nanowires: contact atomic-force microscopy. Phys. Rev. B 73(23), 235409 (2006)

    ADS  MathSciNet  Google Scholar 

  50. R.E. Miller, V.B. Shenoy, Size-dependent elastic properties of nanosized structural elements. Nanotechnology 11(3), 139 (2000)

    ADS  Google Scholar 

  51. G.-F. Wang, X.-Q. Feng, Surface effects on buckling of nanowires under uniaxial compression. Appl. Phys. Lett. 94(14), 141913 (2009)

    ADS  Google Scholar 

  52. M. Gurtin, J. Weissmüller, F. Larche, A general theory of curved deformable interfaces in solids at equilibrium. Philos. Mag. A 78(5), 1093–1109 (1998)

    ADS  Google Scholar 

  53. T. Chen, M.-S. Chiu, C.-N. Weng, Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids. J. Appl. Phys. 100(7), 074308 (2006)

    ADS  Google Scholar 

  54. G.-F. Wang, X.-Q. Feng, Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Appl. Phys. Lett. 90(23), 231904 (2007)

    ADS  Google Scholar 

  55. D. Karlicic et al., Non-local structural mechanics (Wiley, Hoboken, 2015)

    Google Scholar 

  56. G.-F. Wang, X.-Q. Feng, Timoshenko beam model for buckling and vibration of nanowires with surface effects. J. Phys. D Appl. Phys. 42(15), 155411 (2009)

    ADS  Google Scholar 

  57. R.B. Hetnarski, M.R. Eslami, G. Gladwell, Thermal stresses: advanced theory and applications (Springer, Berlin, 2009)

    MATH  Google Scholar 

  58. K.A. Elsibai, H.M. Youssef, State-space approach to vibration of gold nano-beam induced by ramp type heating without energy dissipation in femtoseconds scale. J. Therm. Stresses 34(3), 244–263 (2011)

    Google Scholar 

  59. B. Dingfelder, J. Weideman, An improved Talbot method for numerical Laplace transform inversion. Numer. Algorithms 68(1), 167–183 (2015)

    MathSciNet  MATH  Google Scholar 

  60. R.A. Raja, J. Sunil, R. Maheswaran, Estimation of thermo-physical properties of nanofluids using theoretical correlations. Int. J. Appl. Eng. Res. 13(10), 7950–7953 (2018)

    Google Scholar 

  61. J. Wang, Carbon-nanotube based electrochemical biosensors: a review. Electroanalysis 17(1), 7–14 (2005)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Tabriz, Tabriz, Iran

    Babak Alizadeh Hamidi & Reza Hassannejad

  2. Department of Industrial, Mechanical and Aerospace Engineering, Buein Zahra Technical University, Buein Zahra, Qazvin, Iran

    Seyyed Amirhosein Hosseini

  3. Department of Aerospace Engineering, K.N. Toosi University of Technology, Tehran, Iran

    Farshad Khosravi

Authors
  1. Babak Alizadeh Hamidi
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Seyyed Amirhosein Hosseini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Reza Hassannejad
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Farshad Khosravi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Seyyed Amirhosein Hosseini.

Appendix

Appendix

$$ Q_{1} = \frac{{\sqrt {\frac{{ - 2\left( { - 2} \right)^{1/3} \hat{A}^{2} + 6\left( { - 2} \right)^{1/3} \hat{A}\,\hat{C} - 2\hat{B}\beta^{1/3} + \left( { - 2} \right)^{2/3} \beta^{2/3} }}{{\hat{A}\beta^{1/3} }}} }}{\sqrt 6 } $$
$$ Q_{2} = \frac{1}{2\sqrt 3 }\left( {\sqrt {\frac{1}{{\hat{A}\beta^{1/3} }}\left( {2 \times 2^{1/3} {\text{i}}\left( {{\text{i}} + \sqrt 3 } \right)\hat{B}^{2} + 2^{1/3} \left( {6\hat{A}\left( {\hat{C} - {\text{i}}\sqrt 3 \hat{C}} \right) + 2^{1/3} \left( { - 1 - {\text{i}}\sqrt 3 } \right)\beta^{2/3} } \right) - 4\hat{B}\beta^{1/3} } \right)} } \right) $$
$$ Q_{3} = \frac{{\sqrt {\frac{{2 \times 2^{1/3} \hat{B}^{2} - 6 \times 2^{1/3} \hat{A}\,\hat{C} - 2\hat{B}\beta^{1/3} + 2^{2/3} \beta^{2/3} }}{{\hat{A}\beta^{1/3} }}} }}{\sqrt 6 } $$
$$ \beta = - 2\hat{B}^{3} + 9\hat{A}\hat{B}\hat{C} - 27\hat{A}^{2} \hat{D} + \sqrt {4\left( { - \hat{B}^{2} + 3\hat{A}\hat{C}} \right)^{3} + \left( { - 2\hat{B}^{3} + 9\hat{A}\hat{B}\hat{C} - 27\hat{A}^{2} \hat{D}} \right)^{2} } $$
$$ \varepsilon_{1} = \frac{{ - \mu_{1} }}{{\mu_{4} \chi_{1} }}\,\,\,\,\,\,\,\varepsilon_{2} = \frac{{ - \mu_{2} + \mu_{4} \chi_{2} }}{{\mu_{4} \chi_{1} }}\,\,\,\,\,\,\varepsilon_{3} = \frac{{ - \mu_{3} }}{{\mu_{4} \chi_{1} }} $$
$$ \begin{aligned} \Delta_{1} = \varepsilon_{1} Q_{1}^{4} + \varepsilon_{2} Q_{1}^{2} + \varepsilon_{3} \hfill \\ \Delta_{2} = \varepsilon_{1} Q_{2}^{4} + \varepsilon_{2} Q_{2}^{2} + \varepsilon_{3} \hfill \\ \Delta_{3} = \varepsilon_{1} Q_{3}^{4} + \varepsilon_{2} Q_{3}^{2} + \varepsilon_{3} \hfill \\ \end{aligned} $$
$$ \begin{aligned} V_{1} = \Delta_{1} A_{1} \,\,\,\,V_{2} = \Delta_{1} A_{2} \hfill \\ V_{3} = \Delta_{2} A_{3} \,\,\,\,V_{4} = \Delta_{2} A_{4} \hfill \\ V_{5} = \Delta_{3} A_{5} \,\,\,\,\,V_{6} = \Delta_{3} A_{6} \hfill \\ \end{aligned} $$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hamidi, B.A., Hosseini, S.A., Hassannejad, R. et al. Theoretical analysis of thermoelastic damping of silver nanobeam resonators based on Green–Naghdi via nonlocal elasticity with surface energy effects. Eur. Phys. J. Plus 135, 35 (2020). https://doi.org/10.1140/epjp/s13360-019-00037-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1140/epjp/s13360-019-00037-8

Search

Navigation