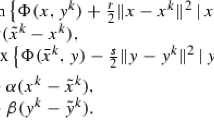A1. PROOF OF LEMMA 1
It is clear that \(g(x) = h\text{*}(Ax)\), where \(h\text{*}\) is the conjugate function to \(h\). By the Demyanov–Danskin theorem, \(\nabla g(x) = {{A}^{{\text{T}}}}y(x)\), where \(y(x) = \left\langle {Ax,y(x)} \right\rangle - h(y(x))\) (i.e., \(y(x) = \mathop {\arg \max }\limits_y \left\{ {\left\langle {Ax,y} \right\rangle - h(y)} \right\}\)).
Let \(h(y)\) be \({{\mu }_{y}}\)-strongly convex. Then, by the choice of \(y(x)\), for all \({{x}_{1}},{{x}_{2}} \in {{Q}_{x}}\), we have
$$\left\langle {A{{x}_{1}},y({{x}_{2}})} \right\rangle - h(y({{x}_{2}})) \leqslant \left\langle {A{{x}_{1}},y({{x}_{1}})} \right\rangle - hy({{x}_{1}}) - \frac{{{{\mu }_{y}}}}{2}\left\| {y({{x}_{2}}) - y({{x}_{1}})} \right\|_{2}^{2},$$
$$\left\langle {A{{x}_{2}},y({{x}_{1}})} \right\rangle - h(y({{x}_{1}})) \leqslant \left\langle {A{{x}_{2}},y({{x}_{2}})} \right\rangle - h(y({{x}_{2}})) - \frac{{{{\mu }_{y}}}}{2}\left\| {y({{x}_{1}}) - y({{x}_{2}})} \right\|_{2}^{2}.$$
After adding these two inequalities, we have
$$\left\langle {A{{x}_{1}} - A{{x}_{2}},y({{x}_{2}}) - y({{x}_{1}})} \right\rangle \leqslant - {{\mu }_{y}}\left\| {y({{x}_{2}}) - y({{x}_{1}})} \right\|_{2}^{2},$$
whence
$${{\mu }_{y}}\left\| {y({{x}_{2}}) - y({{x}_{1}})} \right\|_{2}^{2} \leqslant \left\langle {A{{x}_{2}} - A{{x}_{1}},y({{x}_{2}}) - y({{x}_{1}})} \right\rangle \leqslant {{\left\| {A{{x}_{2}} - A{{x}_{1}}} \right\|}_{2}} \cdot {{\left\| {y({{x}_{2}}) - y({{x}_{1}})} \right\|}_{2}},$$
i.e., for the norm of the matrix, \({{\left\| A \right\|}_{2}}\), we obtain
$${{\left\| {y({{x}_{2}}) - y({{x}_{1}})} \right\|}_{2}} \leqslant \frac{{{{{\left\| A \right\|}}_{2}}{{{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}}_{2}}}}{{{{\mu }_{y}}}}.$$
Therefore,
$${{\left\| {\nabla g({{x}_{1}}) - \nabla g({{x}_{2}})} \right\|}_{2}} \leqslant {{\left\| {{{A}^{{\text{T}}}}} \right\|}_{2}}{{\left\| {y({{x}_{1}}) - y({{x}_{2}})} \right\|}_{2}} \leqslant \frac{{{{{\left\| {{{A}^{{\text{T}}}}A} \right\|}}_{2}}}}{{{{\mu }_{y}}}}{{\left\| {{{x}_{1}} - {{x}_{2}}} \right\|}_{2}} = \frac{{{{\lambda }_{{{{\max}}}}}({{A}^{{\text{T}}}}A)}}{{{{\mu }_{y}}}}{{\left\| {{{x}_{1}} - {{x}_{2}}} \right\|}_{2}}.$$
Let us now check the second part of the assertion. Let \({{x}_{1}},{{x}_{2}} \in \mathop {\left( {\operatorname{Ker} A} \right)}\nolimits^ \bot \).
It is well known that, for the conjugate function
$$h\text{*}{\kern 1pt} (x) = \mathop {\max}\limits_y \left\{ {\left\langle {x,y} \right\rangle - h(y)} \right\} = \langle x,{{\hat {y}}_{x}}\rangle - h({{\hat {y}}_{x}}),$$
we have
$${{\hat {y}}_{x}} \in \partial h\text{*}{\kern 1pt} (x) \Leftrightarrow x \in \partial h({{\hat {y}}_{x}}),$$
whence \((x \to Ax,{{\hat {y}}_{x}} \to y(x))\)
$$y(x) \in \partial h\text{*}{\kern 1pt} (Ax) \Leftrightarrow Ax \in \partial h(y(x)).$$
Then, we have
$$\begin{gathered} \left\langle {\nabla g({{x}_{1}}) - \nabla g({{x}_{2}}),{{x}_{1}} - {{x}_{2}}} \right\rangle = \langle {{A}^{{\text{T}}}}y({{x}_{1}}) - {{A}^{{\text{T}}}}y({{x}_{2}}),{{x}_{1}} - {{x}_{2}}\rangle = \left\langle {y({{x}_{1}}) - y({{x}_{2}}),A{{x}_{1}} - A{{x}_{2}}} \right\rangle \\ \, = \left\langle {A{{x}_{1}} - A{{x}_{2}},y({{x}_{1}}) - y({{x}_{2}})} \right\rangle \geqslant \{ {\text{from}}\;{{L}_{y}}{\text{ - smoothness of}}\;h\} \geqslant \frac{1}{{{{L}_{y}}}}\left\| {A{{x}_{1}} - A{{x}_{2}}} \right\|_{2}^{2} \\ = \frac{1}{{{{L}_{y}}}}\langle {{A}^{{\text{T}}}}A({{x}_{1}} - {{x}_{2}}),{{x}_{1}} - {{x}_{2}}\rangle \geqslant \{ {\text{from}}\;{{x}_{1}} - {{x}_{2}}\not \in \operatorname{Ker} A\;({\text{i}}.{\text{e}}.,\;{{x}_{1}},{{x}_{2}} \in \operatorname{Ker} {{A}^{ \bot }})\} \geqslant \frac{{\lambda _{{\min}}^{ + }({{A}^{{\text{T}}}}A)}}{{{{L}_{y}}}}\left\| {{{x}_{1}} - {{x}_{2}}} \right\|_{2}^{2}, \\ \end{gathered} $$
which justifies the \(\frac{{\lambda _{{\min}}^{ + }({{A}^{{\text{T}}}}A)}}{{{{L}_{y}}}}\)-strong convexity of \(g(x)\) for \(x \in \mathop {\left( {\operatorname{Ker} A} \right)}\nolimits^ \bot \).
A2. PROOF OF LEMMA 2
The function \(\hat {S}(x, \cdot )\) is \({{\mu }_{y}}\)-strongly concave on \({{Q}_{y}}\), and \(\hat {S}( \cdot ,y)\) is differentiable on \({{Q}_{x}}\). Therefore, by Demyanov–Danskin’s theorem, for any \(x \in {{Q}_{x}}\), we have
$$\nabla g(x) = {{\nabla }_{x}}\tilde {S}(x,y\text{*}{\kern 1pt} (x)) = {{\nabla }_{x}}F(x,y\text{*}{\kern 1pt} (x)).$$
(A1)
To prove that \(g(\cdot )\) has an \(L\)-Lipschitz gradient for \(L = {{L}_{{xx}}} + \tfrac{{2L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\), let us prove the Lipschitz condition for \(y\text{*}{\kern 1pt} (\cdot )\) (the function \(y\text{*}\) is defined in (9)) with a constant \(\tfrac{{2{{L}_{{xy}}}}}{{{{\mu }_{y}}}}\).
Since \(\hat {S}({{x}_{1}}, \cdot )\) is \({{\mu }_{y}}\)-strongly concave on \({{Q}_{y}}\), for arbitrary \({{x}_{1}},{{x}_{2}} \in {{Q}_{x}}\),
$$\left\| {y\text{*}{\kern 1pt} ({{x}_{1}}) - y\text{*}{\kern 1pt} ({{x}_{2}})} \right\|_{2}^{2} \leqslant \frac{2}{{{{\mu }_{y}}}}\left( {\hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - \hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right).$$
(A2)
On the other hand, \(\hat {S}({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{1}})) - \hat {S}({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}})) \leqslant 0\), since \(y\text{*}{\kern 1pt} ({{x}_{2}})\) affords the maximum to \(\hat {S}({{x}_{2}},.)\) on \({{Q}_{y}}\). We have
$$\begin{gathered} \hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - \hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}})) \leqslant \left( {\hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - \hat {S}({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right) - \left( {\hat {S}({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{1}})) + \hat {S}({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right) \\ \,\mathop = \limits^{{\text{ from}}\;(7)} \left( {F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right) - \left( {F({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{1}})) - F({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right) \\ \end{gathered} $$
$$\, = \int\limits_0^1 {\left\langle {{{\nabla }_{x}}F({{x}_{1}} + t({{x}_{2}} - {{x}_{1}}),y\text{*}{\kern 1pt} ({{x}_{1}})) - {{\nabla }_{x}}F({{x}_{1}} + t({{x}_{2}} - {{x}_{1}}),y\text{*}{\kern 1pt} ({{x}_{2}})),{{x}_{2}} - {{x}_{1}}} \right\rangle } dt $$
(A3)
$$\begin{gathered} \leqslant {{\left\| {{{\nabla }_{x}}F({{x}_{1}} + t({{x}_{2}} - {{x}_{1}}),y\text{*}{\kern 1pt} ({{x}_{1}})) - {{\nabla }_{x}}F({{x}_{1}} + t({{x}_{2}} - {{x}_{1}}),y\text{*}{\kern 1pt} ({{x}_{1}}))} \right\|}_{2}} \cdot {{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}_{2}}\; \\ \,\mathop \leqslant \limits^{{\text{from}}\;(5)} {{L}_{{xy}}}{{\left\| {y\text{*}{\kern 1pt} ({{x}_{1}}) - y\text{*}{\kern 1pt} ({{x}_{2}})} \right\|}_{2}} \cdot {{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}_{2}}. \\ \end{gathered} $$
Thus, (A2) and (A3) imply the inequality
$${{\left\| {y\text{*}{\kern 1pt} ({{x}_{2}}) - y\text{*}{\kern 1pt} ({{x}_{1}})} \right\|}_{2}} \leqslant \frac{{2{{L}_{{xy}}}}}{{{{\mu }_{y}}}}{{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}_{2}},$$
(A4)
i.e., the function \(y\text{*}{\kern 1pt} (\cdot )\) satisfies the Lipschitz condition with a constant \(\tfrac{{2{{L}_{{xy}}}}}{{{{\mu }_{y}}}}\). Next, from (A1), we obtain
$$\begin{gathered} {{\left\| {\nabla g({{x}_{1}}) - \nabla g({{x}_{2}})} \right\|}_{2}} = {{\left\| {{{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - {{\nabla }_{x}}F({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right\|}_{2}} \\ = {{\left\| {{{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - {{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}})) + {{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}})) - {{\nabla }_{x}}F({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right\|}_{2}} \\ \end{gathered} $$
$$\begin{gathered} \leqslant {{\left\| {{{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{1}})) - {{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right\|}_{2}} + {{\left\| {{{\nabla }_{x}}F({{x}_{1}},y\text{*}{\kern 1pt} ({{x}_{2}})) - {{\nabla }_{x}}F({{x}_{2}},y\text{*}{\kern 1pt} ({{x}_{2}}))} \right\|}_{2}}\; \\ \,\mathop \leqslant \limits^{{\text{from}}\;{\text{(4)}}\;{\text{and}}\;{\text{(5)}}} {{L}_{{xy}}}{{\left\| {y\text{*}{\kern 1pt} ({{x}_{1}}) - y\text{*}{\kern 1pt} ({{x}_{2}})} \right\|}_{2}} + {{L}_{{xx}}}{{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}_{2}}\;\mathop = \limits^{{\text{from}}\;{\text{(A4)}}} \;\left( {{{L}_{{xx}}} + \tfrac{{2L_{{xy}}^{2}}}{{{{\mu }_{y}}}}} \right){{\left\| {{{x}_{2}} - {{x}_{1}}} \right\|}_{2}}. \\ \end{gathered} $$
This means that \(g( \cdot )\) has an \(L\)-Lipschitz gradient with \(L = {{L}_{{xx}}} + \tfrac{{2L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\).
Let us now check the inequalities from (23). First, we prove that, for any \(\delta \geqslant 0\) and \(x \in {{Q}_{x}}\),
$${{\left\| {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) - \nabla g(x)} \right\|}_{2}} \leqslant {{L}_{{xy}}}\sqrt {\frac{{2\delta }}{{{{\mu }_{y}}}}} .$$
(A5)
For any \(x \in {{Q}_{x}}\), it is true that \({{\nabla }_{x}}\hat {S}(x,{{\tilde {y}}_{\delta }}(x)) = {{\nabla }_{x}}F(x,{{\tilde {y}}_{\delta }}(x))\). Then,
$$\begin{gathered} \left\| {{{\nabla }_{x}}\hat {S}(x,{{{\tilde {y}}}_{\delta }}(x)) - \nabla g(x)} \right\|_{2}^{2} = \left\| {{{\nabla }_{x}}F(x,{{{\tilde {y}}}_{\delta }}(x)) - {{\nabla }_{x}}F(x,y\text{*}{\kern 1pt} (x))} \right\|_{2}^{2}\;\mathop \leqslant \limits^{{\text{from}}\;{\text{(5)}}} \;L_{{xy}}^{2}\left\| {y\text{*}{\kern 1pt} (x) - {{{\tilde {y}}}_{\delta }}(x)} \right\|_{2}^{2}\; \\ \,\mathop \leqslant \limits^{{\text{from}}\;{\text{(A2)}}} \frac{{2L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\left( {\hat {S}(x,y\text{*}{\kern 1pt} (x)) - \hat {S}(x,{{{\tilde {y}}}_{\delta }}(x))} \right)\;\mathop \leqslant \limits^{{\text{from}}\;{\text{(10)}}} \;\frac{{2\delta L_{{xy}}^{2}}}{{{{\mu }_{y}}}}, \\ \end{gathered} $$
which justifies inequality (A5).
Now, due to the \({{\mu }_{x}}\)-strong convexity of \(\hat {S}( \cdot ,\mathop {\tilde {y}}\nolimits_\delta (x))\) on \({{Q}_{x}}\), for arbitrary \(x,z \in {{Q}_{x}}\), it is true that
$$g(z)\;\mathop \leqslant \limits^{{\text{ from}}\;{\text{(8)}}} \;\hat {S}(z,\mathop {\tilde {y}}\nolimits_\delta (x)) \geqslant \hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),z - x} \right\rangle .$$
Thus,
$$0 \geqslant \hat {S}(x,{{\tilde {y}}_{\delta }}(x)) - g(z) + \left\langle {{{\nabla }_{x}}\hat {S}(x,{{{\tilde {y}}}_{\delta }}(x)),z - x} \right\rangle ,$$
which proves the left-hand side of (23). To prove the right-hand side of (23), note that \(g\) is convex and has an \(L\)-Lipschitz gradient on \({{Q}_{x}}\). Therefore, for arbitrary \(x,z \in {{Q}_{x}}\), we have
$$\begin{gathered} g(z) \leqslant g(x) + \left\langle {\nabla g(x),z - x} \right\rangle + \;\frac{L}{2}\left\| {z - x} \right\|_{2}^{2}\;\mathop \leqslant \limits^{{\text{from}}\;{\text{(10)}}} \;\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + \delta + \tfrac{L}{2}\left\| {z - x} \right\|_{2}^{2} \\ + \;\left\langle {\nabla g(x),z - x} \right\rangle + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),x - z} \right\rangle - \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),x - z} \right\rangle = \hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + \delta \\ \end{gathered} $$
$$\begin{gathered} \, + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),z - x} \right\rangle + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) - \nabla g(x),x - z} \right\rangle + \tfrac{L}{2}\left\| {z - x} \right\|_{2}^{2}\; \\ \,\mathop \leqslant \limits^{{\text{from}}\;{\text{(A5)}}} \hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + \delta + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),z - x} \right\rangle + {{L}_{{xy}}}\sqrt {\tfrac{{2\delta }}{{{{\mu }_{y}}}}} \cdot {{\left\| {z - x} \right\|}_{2}} + \tfrac{L}{2}\left\| {z - x} \right\|_{2}^{2}. \\ \end{gathered} $$
However,
$${{L}_{{xy}}}\sqrt {\tfrac{{2\delta }}{{{{\mu }_{y}}}}} \cdot {{\left\| {z - x} \right\|}_{2}} \leqslant \tfrac{{2\sqrt \delta {{L}_{{xy}}}}}{{\sqrt {{{\mu }_{y}}} }}{{\left\| {z - x} \right\|}_{2}} = 2\sqrt {\tfrac{{L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\left\| {z - x} \right\|_{2}^{2} \cdot \delta } \leqslant \tfrac{{L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\left\| {z - x} \right\|_{2}^{2} + \delta $$
due to the classical inequality between the arithmetic and geometric mean. Therefore,
$$g(z) \leqslant \hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + 2\delta + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),z - x} \right\rangle + \tfrac{{L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\left\| {z - x} \right\|_{2}^{2} + \tfrac{L}{2}\left\| {z - x} \right\|_{2}^{2},$$
and, since \(L = {{L}_{{xx}}} + \tfrac{{2L_{{xy}}^{2}}}{{{{\mu }_{y}}}}\), we have \(\tfrac{{L_{{xy}}^{2}}}{{{{\mu }_{y}}}} \leqslant \tfrac{L}{2}\); therefore,
$$g(z) \leqslant \hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)) + \left\langle {{{\nabla }_{x}}\hat {S}(x,\mathop {\tilde {y}}\nolimits_\delta (x)),z - x} \right\rangle + 2\delta + L\left\| {z - x} \right\|_{2}^{2}.$$
Thus, we have
$$g(z) - \hat {S}(x,{{\tilde {y}}_{\delta }}x)) - \left\langle {{{\nabla }_{x}}\hat {S}(x,{{{\tilde {y}}}_{\delta }}(x)),z - x} \right\rangle \leqslant L\left\| {z - x} \right\|_{2}^{2} + 2\delta ,$$
which implies the left-hand side of inequality (23).
A3. PROOF OF LEMMA 3
Recall that Lemma 3 considers the minimization problem
$$\mathop {\min}\limits_{x \in {{\mathbb{R}}^{n}}} P(x): = r(x) + g(x),$$
(A6)
where the function \(r(x)\) is \({{\mu }_{r}}\)-strongly convex and \({{L}_{r}}\)-smooth for \({{L}_{r}} \geqslant {{\mu }_{r}} \geqslant 0\), the function \(g(x)\) is \({{\mu }_{g}}\)-strongly convex and \({{L}_{g}}\)-smooth for \({{L}_{g}} \geqslant {{\mu }_{g}} \geqslant 0\), and the function \(P(x)\) is \(\mu \)-strongly convex and \(L\)-smooth with \(L = {{L}_{r}} + {{L}_{g}} \geqslant \mu = {{\mu }_{r}} + {{\mu }_{g}} > 0\). Denote by \(x\text{*}\) the sought-for minimum point of the functional P.
Let us prove Lemma 3 under the assumption that the function \(r(x)\) admits at an arbitrary requested point a \(({{\delta }_{r}},{{L}_{r}},{{\mu }_{r}})\)-gradient \(\nabla {{r}_{{{{\delta }_{r}}}}}(x)\) and the function \(g(x)\) admits a \(({{\delta }_{g}},{{L}_{g}},{{\mu }_{g}})\)-gradient \(\nabla {{g}_{{{{\delta }_{g}}}}}(x)\). This means that, for arbitrary \(x,y \in {{\mathbb{R}}^{n}}\), we have the following inequalities:
$$\begin{gathered} \frac{{{{\mu }_{r}}}}{2} - \left\| {x - y} \right\|_{2}^{2} - {{\delta }_{r}} \leqslant r(x) - r(y) - \left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}(y),x - y} \right\rangle \leqslant \frac{{{{L}_{r}}}}{2}\left\| {x - y} \right\|_{2}^{2} + {{\delta }_{r}}, \\ \frac{{{{\mu }_{g}}}}{2} - \left\| {x - y} \right\|_{2}^{2} - {{\delta }_{g}} \leqslant g(x) - g(y) - \left\langle {\nabla {{g}_{{{{\delta }_{g}}}}}(y),x - y} \right\rangle \leqslant \frac{{{{L}_{g}}}}{2}\left\| {x - y} \right\|_{2}^{2} + {{\delta }_{g}}, \\ \end{gathered} $$
(A7)
where \({{\delta }_{r}} \geqslant 0\) and \({{\delta }_{g}} \geqslant 0\).
In fact, to justify the main results of the work, the statement of Lemma 3 for the less restrictive concept of the (\(\delta ,L\)) -gradient under the assumption of strong convexity of \(g\) and \(r\) is sufficient. Since it is assumed that both \(r\) and \(g\) allows inexact values of the gradients at the requested points, we can set, for definiteness, \({{L}_{r}} \leqslant {{L}_{g}}\).
Algorithm 5. Accelerated proximal gradient method with inexact gradient values.
1: Parameters: \({{x}^{0}} \in {{\mathbb{R}}^{n}}\), steps \(\alpha ,\beta \in (0,1)\), \(\eta > 0\).
2: \({{y}^{0}} = {{z}^{0}} = {{x}^{0}}\).
3: for \(k = 0,1,2, \ldots \) do
4: \({{x}^{k}} = \alpha {{z}^{k}} + (1 - \alpha ){{y}^{k}}\)
5: \({{y}^{{k + 1}}} \approx \mathop {\hat {y}}\nolimits^{k + 1} : = \mathop {{\text{prox}}}\nolimits_{\tfrac{1}{{{{L}_{r}}}}g(\cdot )} \left( {{{x}^{k}} - \tfrac{1}{{{{L}_{r}}}}\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}})} \right)\) (\({{y}^{{k + 1}}}\) is the approximate value of this operator, found by solving an auxiliary optimization problem by the fast gradient method)
6: \({{z}^{{k + 1}}} = \beta {{z}^{k}} + (1 - \beta ){{x}^{k}} + \eta ({{y}^{{k + 1}}} - {{x}^{k}})\).
7: end for
We will apply to considered problem (A6) the following method, which implies solving an auxiliary subproblem by a fast gradient method under the condition of an inexactness specified (\({{\delta }_{g}},{{L}_{g}},{{\mu }_{g}}\))-gradient of \(g\).
Let us prove a necessary auxiliary estimate for the parameters \({{x}^{k}}\) and \({{y}^{{k + 1}}}\) for an arbitrary \(x \in {{\mathbb{R}}^{n}}\).
Proposition 1. For any \(x \in {{\mathbb{R}}^{n}}\), it is true that
$$\begin{gathered} \left\langle {{{x}^{k}}\, - \,{{y}^{{k + 1}}},x\, - \,{{x}^{k}}} \right\rangle \,\; \leqslant \;\,\frac{1}{{{{L}_{r}} + {{\mu }_{g}}}}\left[ {P(x)\,\; - \;\,P({{y}^{{k + 1}}})\,\; - \,\;\frac{\mu }{4}\,\left\| {x - {{x}^{k}}} \right\|_{2}^{2}\, - \;\,\frac{{{{L}_{r}} + {{\mu }_{g}}}}{4}\left\| {\mathop {\hat {y}}\nolimits^{k + 1} \, - \,{{x}^{k}}} \right\|_{2}^{2}\, + \,2{{\delta }_{r}}} \right]\, \\ + \;{{c}_{1}}\left\| {{{y}^{{k + 1}}}\, - \,{{y}^{{k + 1}}}} \right\|_{2}^{2}, \\ \end{gathered} $$
(A8)
where the constant \({{c}_{1}}\) is defined as follows:
$${{c}_{1}} = 2\left[ {\frac{{{{L}_{r}}}}{\mu } + 1} \right]\left[ {\frac{{L_{g}^{2}}}{{L_{r}^{2}}} + 1} \right].$$
Proof. By the definition of \({{\hat {y}}^{{k + 1}}}\),
$$\mathop {\hat {y}}\nolimits^{k + 1} = {{x}^{k}} - \frac{1}{{{{L}_{r}}}}\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) - \frac{1}{{{{L}_{r}}}}\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ).$$
By assumption (A7) and the \({{\mu }_{g}}\)-strong convexity of the function \(g(x)\), we have
$$\begin{gathered} \left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle = \left\langle {{{x}^{k}} - \mathop {\hat {y}}\nolimits^{k + 1} + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle = \frac{1}{{{{L}_{r}}}}\left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) + \nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ),x - {{x}^{k}}} \right\rangle \\ \, + \left\langle {\mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle = \frac{1}{{{{L}_{r}}}}\left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) + \nabla g({{y}^{{k + 1}}}),x - {{x}^{k}}} \right\rangle \\ + \;\left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ) - \nabla g({{y}^{{k + 1}}})] + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle = \frac{1}{{{{L}_{r}}}}\left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}),x - {{x}^{k}}} \right\rangle + \frac{1}{{{{L}_{r}}}}\left\langle {\nabla g({{y}^{{k + 1}}}),x - {{y}^{{k + 1}}}} \right\rangle \\ \end{gathered} $$
$$\begin{gathered} + \;\frac{1}{{{{L}_{r}}}}\left\langle {\nabla g({{y}^{{k + 1}}}),{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + \left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ) - \nabla g({{y}^{{k + 1}}})] + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle \\ \, \leqslant \frac{1}{{{{L}_{r}}}}\left[ {r(x) - r({{x}^{k}}) - \frac{{{{\mu }_{r}}}}{2}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} + {{\delta }_{r}}} \right] + \frac{1}{{{{L}_{r}}}}\left[ {g(x) - g({{y}^{{k + 1}}}) - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2}} \right] \\ + \;\frac{1}{{{{L}_{r}}}}\left\langle {\nabla g({{y}^{{k + 1}}}),{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + \left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ) - \nabla g({{y}^{{k + 1}}})] + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle . \\ \end{gathered} $$
Next, we apply the right-hand side of inequality (A7) to \(r(x)\):
$$r({{y}^{{k + 1}}}) \leqslant r({{x}^{k}}) + \left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}),{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + \frac{{{{L}_{r}}}}{2}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + {{\delta }_{r}},$$
whence
$$\begin{gathered} \left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle \leqslant \frac{1}{{{{L}_{r}}}}\left[ {r(x) - r({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}}}}{2}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] + \frac{1}{{{{L}_{r}}}}\left[ {g(x) - g({{y}^{{k + 1}}}) - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2}} \right] \\ + \;\frac{1}{{{{L}_{r}}}}\left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) + \nabla g({{y}^{{k + 1}}}),{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + \frac{1}{2}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + \left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ) - \nabla g({{y}^{{k + 1}}})] + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle \\ \end{gathered} $$
$$\begin{gathered} = \frac{1}{{{{L}_{r}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}}}}{2}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \frac{{{{L}_{r}}}}{2}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] \\ + \;\frac{1}{{{{L}_{r}}}}\left\langle {\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) + \nabla g({{y}^{{k + 1}}}),{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + \left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} ) - \nabla g({{y}^{{k + 1}}})] + \mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle \\ \end{gathered} $$
$$\begin{gathered} = \frac{1}{{{{L}_{r}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}}}}{2}\left\| {x - {{x}^{{k + 1}}}} \right\|_{2}^{2} - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \frac{{{{L}_{r}}}}{2}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] \\ + \;\left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} )\, - \,\nabla g({{y}^{{k + 1}}})]\, + \,\mathop {\hat {y}}\nolimits^{k + 1} \, - \,{{y}^{{k + 1}}},{{x}^{k}}\, - \,{{y}^{{k + 1}}}} \right\rangle + \left\langle {\frac{1}{{{{L}_{r}}}}[\nabla g(\mathop {\hat {y}}\nolimits^{k + 1} )\, - \,\nabla g({{y}^{{k + 1}}})]\, + \,\mathop {\hat {y}}\nolimits^{k + 1} \, - \,{{y}^{{k + 1}}},x\, - \,{{x}^{k}}} \right\rangle . \\ \end{gathered} $$
We now apply Young’s inequality, as well as the \({{L}_{g}}\)-Lipschitz continuity of the gradient \(\nabla g(x)\):
$$\left\| {\nabla g({{y}^{{k + 1}}}) - \nabla g(\mathop {\hat {y}}\nolimits^{k + 1} )} \right\|_{2}^{2} \leqslant L_{g}^{2}\left\| {\mathop {\hat {y}}\nolimits^{k + 1} - {{y}^{{k + 1}}}} \right\|_{2}^{2};$$
$$\left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle \leqslant \frac{1}{{{{L}_{r}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}}}}{2}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \frac{{{{L}_{r}}}}{2}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] $$
$$ + \;\frac{{2{{\delta }_{r}}}}{{{{L}_{r}}}} + \frac{\mu }{{4{{L}_{r}}}}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} + \frac{{{{L}_{r}} + {{\mu }_{g}}}}{{4{{L}_{r}}}}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + \left[ {\frac{{{{L}_{r}}}}{\mu } + \frac{{{{L}_{r}}}}{{{{L}_{r}} + {{\mu }_{g}}}}} \right]\left\| {\frac{1}{{{{L}_{r}}}}[\nabla g({{{\hat {y}}}^{{k + 1}}}) - \nabla g({{y}^{{k + 1}}})] + {{{\hat {y}}}^{{k + 1}}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} $$
$$ \leqslant \frac{1}{{{{L}_{r}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}} - {{\mu }_{g}}}}{4}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{\mu }_{g}}}}{2}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \frac{{{{L}_{r}} - {{\mu }_{g}}}}{4}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] $$
$$ + \;\frac{{2{{\delta }_{r}}}}{{{{L}_{r}}}} + 2\left[ {\frac{{{{L}_{r}}}}{\mu } + \frac{{{{L}_{r}}}}{{{{L}_{r}} + {{\mu }_{g}}}}} \right]\left[ {\frac{{L_{g}^{2}}}{{L_{r}^{2}}} + 1} \right]\left\| {{{{\hat {y}}}^{{k + 1}}} - {{y}^{{k + 1}}}} \right\|_{2}^{2}.$$
Finally, we make the final transformations:
$$\left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle = \frac{{{{L}_{r}}}}{{{{L}_{r}} + {{\mu }_{g}}}}\left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle + \frac{{{{\mu }_{g}}}}{{{{L}_{r}} + {{\mu }_{g}}}}\left\langle {{{x}^{k}} - {{y}^{{k + 1}}},x - {{x}^{k}}} \right\rangle $$
$$ \leqslant \frac{1}{{{{L}_{r}} + {{\mu }_{g}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}} - {{\mu }_{g}}}}{4}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{L}_{r}} - {{\mu }_{g}}}}{4}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] - \frac{{{{\mu }_{g}}}}{{2\left( {{{L}_{r}} + {{\mu }_{g}}} \right)}}\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} $$
$$ + \;\frac{{2{{L}_{r}}}}{{{{L}_{r}} + {{\mu }_{g}}}}\left[ {\frac{{{{L}_{r}}}}{\mu } + \frac{{{{L}_{r}}}}{{{{L}_{r}} + {{\mu }_{g}}}}} \right]\left[ {\frac{{L_{g}^{2}}}{{L_{r}^{2}}} + 1} \right]\left\| {{{{\hat {y}}}^{{k + 1}}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} + \frac{{{{\mu }_{g}}}}{{2\left( {{{L}_{r}} + {{\mu }_{g}}} \right)}}\left[ {\left\| {x - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \left\| {{{x}^{k}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} - \left\| {x - {{x}^{k}}_{2}^{2}} \right\|} \right] $$
$$ \leqslant \frac{1}{{{{L}_{r}} + {{\mu }_{g}}}}\left[ {P(x) - P({{y}^{{k + 1}}}) - \frac{{{{\mu }_{r}} + {{\mu }_{g}}}}{4}\left\| {x - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{L}_{r}} + {{\mu }_{g}}}}{4}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] $$
$$ + \;2\left[ {\frac{{{{L}_{r}}}}{\mu } + 1} \right]\left[ {\frac{{L_{g}^{2}}}{{L_{r}^{2}}} + 1} \right]\left\| {{{{\hat {y}}}^{{k + 1}}} - {{y}^{{k + 1}}}} \right\|_{2}^{2}.$$
Proposition 2. Suppose that the following values of the parameters of algorithm 5 are chosen:
$$\eta = \frac{{2({{L}_{r}} + {{\mu }_{g}})}}{{8\alpha ({{L}_{r}} + {{\mu }_{g}}) + (1 - \alpha )\mu }},$$
$$\beta = 1 - \frac{{\eta \mu }}{{2({{L}_{r}} + {{\mu }_{g}})}} = 1 - \frac{\mu }{{8\alpha ({{L}_{r}} + {{\mu }_{g}}) + (1 - \alpha )\mu }},$$
$$\alpha = \frac{1}{4}\sqrt {\frac{\mu }{{{{L}_{r}} + {{\mu }_{g}}}}} \leqslant \frac{1}{4}.$$
Then, we have the following inequality:
$$\begin{gathered} \left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{{k + 1}}}) - P(x{\kern 1pt} {\text{*}})] \leqslant \left( {1 - \alpha } \right)\left( {\left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{{k + 1}}}) - P(x{\kern 1pt} {\text{*}})]} \right) \\ + \;{{c}_{3}}\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - {{{\hat {y}}}^{{k + 1}}}} \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + 4{{c}_{2}}{{\delta }_{r}}, \\ \end{gathered} $$
(A9)
where \({{c}_{2}}\) and \({{c}_{3}}\) are some positive constants.
Proof. Let us estimate the quantity \(\left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2}\):
$$\begin{gathered} \left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} = \left\| {\beta {{z}^{k}} + (1 - \beta ){{x}^{k}} - x{\kern 1pt} {\text{*}} + \eta ({{y}^{{k + 1}}} - {{x}^{k}})} \right\|_{2}^{2} = \left\| {\beta ({{z}^{k}} - x{\kern 1pt} {\text{*}}) + (1 - \beta )({{x}^{k}} - x{\kern 1pt} {\text{*}})} \right\|_{2}^{2} \\ + \;{{\eta }^{2}}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2\eta \left\langle {\beta {{z}^{k}} + (1 - \beta ){{x}^{k}} - x\text{*},{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle \leqslant \beta \left\| {{{z}^{k}} - x{\kern 1pt} {\text{*}}} \right\|_{2}^{2} + (1 - \beta )\left\| {{{x}^{k}} - x\text{*}} \right\|_{2}^{2} \\ \end{gathered} $$
$$\begin{gathered} \, + {{\eta }^{2}}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2\eta \beta \left\langle {{{z}^{k}} - {{x}^{k}},{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + 2\eta \left\langle {{{x}^{k}} - x\text{*},{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle \leqslant \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} \\ + \;(1 - \beta )\left\| {{{x}^{k}} - x\text{*}} \right\|_{2}^{2} + {{\eta }^{2}}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2\eta \beta \frac{{1 - \alpha }}{\alpha }\left\langle {{{x}^{k}} - {{y}^{k}},{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle + 2\eta \left\langle {{{x}^{k}} - x\text{*},{{y}^{{k + 1}}} - {{x}^{k}}} \right\rangle . \\ \end{gathered} $$
We apply twice inequality (A8):
$$\begin{gathered} \left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} \leqslant \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + (1 - \beta )\left\| {{{x}^{k}} - x\text{*}} \right\|_{2}^{2} + {{\eta }^{2}}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} \\ + \;2\beta \frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}\frac{{1 - \alpha }}{\alpha }\left[ {P({{y}^{k}}) - P({{y}^{{k + 1}}}) - \frac{{{{L}_{r}} + {{\mu }_{g}}}}{4}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] \\ + \;2\frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}\left[ {P(x{\kern 1pt} {\text{*}}) - P({{y}^{{k + 1}}}) - \frac{\mu }{4}\left\| {x{\kern 1pt} {\text{*}} - {{x}^{k}}} \right\|_{2}^{2} - \frac{{{{L}_{r}} + {{\mu }_{g}}}}{4}\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2{{\delta }_{r}}} \right] \\ \end{gathered} $$
$$\begin{gathered} + \;2\eta {{c}_{1}}\left[ {\beta \frac{{1 - \alpha }}{\alpha } + 1} \right]\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} = \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + \left[ {1 - \beta - \frac{{\eta \mu }}{{2({{L}_{r}} + {{\mu }_{g}})}}} \right]\left\| {{{x}^{k}} - x\text{*}} \right\|_{2}^{2} \\ + \;\left[ {{{\eta }^{2}} - \frac{{\eta \beta }}{4}\frac{{1 - \alpha }}{\alpha } - \frac{\eta }{4}} \right]\left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2} + 2\beta \frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}\frac{{1 - \alpha }}{\alpha }[P({{y}^{k}}) - P({{y}^{{k + 1}}})] \\ \end{gathered} $$
$$\begin{gathered} + \;2\frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}[P(x{\kern 1pt} {\text{*}}) - P({{y}^{{k + 1}}})] + \frac{\eta }{4}\left[ {\beta \frac{{1 - \alpha }}{\alpha } + 1} \right]\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] \\ \, + 2{{\delta }_{r}}\left[ {2\beta \frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}\frac{{1 - \alpha }}{\alpha } + 2\frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}} \right]. \\ \end{gathered} $$
With the chosen values of the parameters \(\beta \) and \(\eta \) and
$${{c}_{2}} = \frac{{2\eta \beta }}{{\alpha \left( {{{L}_{r}} + {{\mu }_{g}}} \right)}},\quad {{c}_{3}} = \frac{\eta }{4}\left[ {\beta \frac{{1 - \alpha }}{\alpha } + 1} \right],$$
we obtain
$$\begin{gathered} \left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} \leqslant \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + 2\beta \frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}\frac{{1 - \alpha }}{\alpha }[P({{y}^{k}}) - P({{y}^{{k + 1}}})] + 2\frac{\eta }{{{{L}_{r}} + {{\mu }_{g}}}}[P(x{\kern 1pt} {\text{*}}) - P({{y}^{{k + 1}}})] \\ + \;{{c}_{3}}\left[ {8c\left\| {{{y}_{1}}^{{k + 1}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + \frac{{4{{\delta }_{r}}\eta }}{{\alpha ({{L}_{r}} + {{\mu }_{g}})}} \leqslant \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + \frac{{2\beta \eta }}{{{{L}_{r}} + {{\mu }_{g}}}}\frac{{1 - \alpha }}{\alpha }[P({{y}^{k}}) - P({{y}^{{k + 1}}})] \\ \end{gathered} $$
$$\begin{gathered} + \;\frac{{2\beta \eta }}{{{{L}_{r}} + {{\mu }_{g}}}}[P(x\text{*}) - P({{y}^{{k + 1}}})] + {{c}_{3}}\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + \frac{{4{{\delta }_{r}}\eta }}{{\alpha ({{L}_{r}} + {{\mu }_{g}})}} \\ = \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}(1 - \alpha )[P({{y}^{k}}) - P({{y}^{{k + 1}}})] + {{c}_{2}}\alpha [P(x{\kern 1pt} {\text{*}}) - P({{y}^{{k + 1}}})] \\ \end{gathered} $$
$$\begin{gathered} + \;{{c}_{3}}\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + \frac{{2{{c}_{2}}{{\delta }_{r}}}}{\beta } = \beta \left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}(1 - \alpha )[P({{y}^{k}}) - P(x{\kern 1pt} {\text{*}})] \\ \, + {{c}_{2}}[P(x{\kern 1pt} {\text{*}}) - P({{y}^{{k + 1}}})] + {{c}_{3}}\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + \frac{{2{{c}_{2}}{{\delta }_{r}}}}{\beta }. \\ \end{gathered} $$
Using the value of the parameter \(\alpha \), we obtain
$$\frac{1}{2} \leqslant \beta = 1 - \frac{\mu }{{2\sqrt {({{L}_{r}} + {{\mu }_{g}})\mu } + (1 - \alpha )\mu }} \leqslant 1 - \frac{1}{3}\sqrt {\frac{\mu }{{{{L}_{r}} + {{\mu }_{g}}}}} \leqslant 1 - \alpha ,$$
whence
$$\begin{gathered} \left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{{k + 1}}}) - P(x{\kern 1pt} {\text{*}})] \leqslant (1 - \alpha )\left( {\left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{k}}) - P(x\text{*})]} \right) \\ \, + {{c}_{3}}\left[ {8{{c}_{1}}\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} - \left\| {{{y}^{{k + 1}}} - {{x}^{k}}} \right\|_{2}^{2}} \right] + 4{{c}_{2}}{{\delta }_{r}}. \\ \end{gathered} $$
Now we take into account that the auxiliary problem in line 5 of algorithm 5 is solved by the fast gradient method with an inexactness specified gradient of \(g\). Let us estimate the required accuracy \({{\delta }_{g}}\) of the gradient of \(g\) to obtain the required quality of the solution of the problem in the function.
Proposition 3. Let the approximation \({{y}^{{k + 1}}}\) of the proxy operator \(\mathop {\hat {y}}\nolimits^{k + 1} = \mathop {{\text{prox}}}\nolimits_{\tfrac{1}{{{{L}_{r}}}}g(\cdot )} \left( {{{x}^{k}} - \tfrac{1}{{{{L}_{r}}}}\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}})} \right)\) (line 5 of algorithm 5) be calculated by the fast gradient method under the assumption that the (\({{\delta }_{g}},{{\mu }_{g}},{{L}_{g}}\))-gradient of \(g\) is available at an arbitrary requested point [29]. In this case, the minimization problem to be solved has the form
$$\mathop {\min}\limits_{x \in {{\mathbb{R}}^{n}}} g(x) + \frac{{{{L}_{r}}}}{2}\left\| {{{x}^{k}} - \frac{1}{{{{L}_{r}}}}\nabla {{r}_{{{{\delta }_{r}}}}}({{x}^{k}}) - x} \right\|_{2}^{2},$$
(A10)
where \({{x}^{k}}\) is the initial approximation. Then, it is known [29] that, for an arbitrary \(\delta \in (0;1)\), after
$$T = O\left( {\sqrt {\frac{{{{L}_{r}} + {{L}_{g}}}}{{{{L}_{r}} + {{\mu }_{g}}}}} \log\frac{{{{L}_{r}} + {{L}_{g}}}}{{\delta ({{L}_{r}} + {{\mu }_{g}})}}} \right),$$
iterations of the method, the inequality
$$\left\| {{{y}^{{k + 1}}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} \leqslant \delta \left\| {{{x}^{k}} - \mathop {\hat {y}}\nolimits^{k + 1} } \right\|_{2}^{2} + {{c}_{4}}{{\delta }_{g}},$$
(A11)
will be guaranteed with a constant \({{c}_{4}}\) defined as
$${{c}_{4}} = \frac{{4\sqrt {{{L}_{r}} + {{L}_{g}}} }}{{({{L}_{r}} + {{\mu }_{g}})\sqrt {{{L}_{r}} + {{\mu }_{g}}} }}.$$
Proof. Note that the objective function of problem (A10) is \(({{L}_{r}} + {{\mu }_{g}})\)-strongly convex and \(({{L}_{r}} + {{L}_{g}})\)-smooth and \(\mathop {\hat {y}}\nolimits^{k + 1} \) is the exact solution of problem (A10). Inequality (A11) follows from the corresponding result for the fast gradient method in the (\({{\delta }_{g}},{{\mu }_{g}},{{L}_{g}}\))-oracle concept for \(g\) [29].
Proof of Lemma 3. Choosing in inequality (A11) \(\delta = \tfrac{1}{{32{{c}_{1}}}} \leqslant \tfrac{1}{4}\), we obtain
$$\left\| {{{y}^{{k + 1}}} - {{{\hat {y}}}^{{k + 1}}}} \right\|_{2}^{2} \leqslant 2\delta \left( {\left\| {{{x}^{k}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} + \left\| {{{y}^{{k + 1}}} - {{{\hat {y}}}^{{k + 1}}}} \right\|_{2}^{2}} \right) + {{c}_{4}}{{\delta }_{g}} \leqslant 2\delta \left\| {{{x}^{k}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} + \frac{1}{2}\left\| {{{y}^{{k + 1}}} - {{{\hat {y}}}^{{k + 1}}}} \right\|_{2}^{2} + {{c}_{4}}{{\delta }_{g}},$$
whence
$$\left\| {{{y}^{{k + 1}}} - {{{\hat {y}}}^{{k + 1}}}} \right\|_{2}^{2} \leqslant 4\delta \left\| {{{x}^{k}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} + 2{{c}_{4}}{{\delta }_{g}} \leqslant \frac{1}{{8{{c}_{1}}}}\left\| {{{x}^{k}} - {{y}^{{k + 1}}}} \right\|_{2}^{2} + 2{{c}_{4}}{{\delta }_{g}}.$$
Due to inequalities proved above, (A9) means that
$$\left\| {{{z}^{{k + 1}}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{{k + 1}}}) - P(x {\text{*}})] \leqslant (1 - \alpha )\left( {\left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{k}}) - P(x{\kern 1pt} {\text{*}})]} \right) + 4{{c}_{2}}{{\delta }_{r}} + 2{{c}_{3}}{{c}_{4}}{{\delta }_{g}},$$
whence, after telescoping, we have
$$\left\| {{{z}^{k}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{y}^{k}}) - P(x{\kern 1pt} {\text{*}})] \leqslant {{(1 - \alpha )}^{k}}\left( {\left\| {{{x}^{0}} - x\text{*}} \right\|_{2}^{2} + {{c}_{2}}[P({{x}^{0}}) - P(x\text{*})]} \right) + \frac{{4{{c}_{2}}{{\delta }_{r}} + 2{{c}_{3}}{{c}_{4}}{{\delta }_{g}}}}{\alpha }.$$
Taking into account the \(\mu \)-strong convexity of the function \(P(x)\), we have
$$\begin{gathered} P({{y}^{k}}) - P(x{\kern 1pt} {\text{*}}) \leqslant {{(1 - \alpha )}^{k}}\left( {1 + \frac{2}{{\mu {{c}_{2}}}}} \right)[P({{x}^{0}}) - P(x {\text{*}})] + \frac{{4{{\delta }_{r}}}}{\alpha } + \frac{{2{{c}_{3}}{{c}_{4}}{{\delta }_{g}}}}{{{{c}_{2}}\alpha }} \\ \, \leqslant 2{{(1 - \alpha )}^{k}}[P({{x}^{0}}) - P(x {\text{*}})] + \frac{{4{{\delta }_{r}}}}{\alpha } + \frac{{2{{c}_{3}}{{c}_{4}}{{\delta }_{g}}}}{{{{c}_{2}}\alpha }}. \\ \end{gathered} $$
Choosing the number of iterations of the external method
$$k = \frac{1}{\alpha }\log\frac{{4(P({{x}^{0}}) - P(x{\kern 1pt} {\text{*}}))}}{\varepsilon } = O\left( {\sqrt {\frac{{{{L}_{r}} + {{\mu }_{g}}}}{\mu }} \log\frac{1}{\varepsilon }} \right),$$
the accuracy of the \(({{\delta }_{r}},{{L}_{r}},{{\mu }_{r}})\)-gradient \(\nabla {{r}_{{{{\delta }_{r}}}}}(x)\)
$${{\delta }_{r}} = \frac{{\alpha \varepsilon }}{{16}} = O\left( {\sqrt {\frac{\mu }{{{{L}_{r}} + {{\mu }_{g}}}}} \varepsilon } \right),$$
and the accuracy of the \(({{\delta }_{g}},{{L}_{g}},{{\mu }_{g}})\)-gradient \(\nabla {{g}_{{{{\delta }_{g}}}}}(x)\)
$$\begin{gathered} {{\delta }_{g}} = \frac{{\alpha {{c}_{2}}\varepsilon }}{{8{{c}_{3}}{{c}_{4}}}} = \frac{{\alpha \varepsilon }}{{8{{c}_{4}}}}\frac{{2\eta \beta }}{{\alpha ({{L}_{r}} + {{\mu }_{g}})}}\frac{{4\alpha }}{{\eta [(1 - \alpha )\beta + \alpha ]}} \leqslant \frac{{\alpha \varepsilon }}{{{{c}_{4}}(1 - \alpha )({{L}_{r}} + {{\mu }_{g}})}} = \frac{{\sqrt {{{L}_{r}} + {{\mu }_{g}}} \alpha \varepsilon }}{{4(1 - \alpha )\sqrt {{{L}_{r}} + {{L}_{g}}} }} \\ \, = \frac{{\sqrt {{{L}_{r}} + {{\mu }_{g}}} \sqrt \mu \varepsilon }}{{16(1 - \alpha )\sqrt {{{L}_{r}} + {{L}_{g}}} \sqrt {{{L}_{r}} + {{\mu }_{g}}} }} \leqslant \frac{\varepsilon }{{12}}\sqrt {\frac{\mu }{{{{L}_{r}} + {{L}_{g}}}}} = O\left( {\sqrt {\frac{\mu }{{{{L}_{g}} + {{\mu }_{r}}}}} \varepsilon } \right), \\ \end{gathered} $$
where, in the last equality, it is assumed that \({{L}_{r}} \leqslant {{L}_{g}}\) and \(\alpha \leqslant \tfrac{1}{4}\), we obtain the required quality of solution,
$$P({{y}^{k}}) - P(x{\kern 1pt} {\text{*}}) \leqslant \varepsilon .$$
In this case, the number of calls of the \(({{\delta }_{r}},{{L}_{r}},{{\mu }_{r}})\)-gradient \(\nabla {{r}_{{{{\delta }_{r}}}}}(x)\) is
$$k = O\left( {\sqrt {\frac{{{{L}_{r}} + {{\mu }_{g}}}}{\mu }} \log\frac{1}{\varepsilon }} \right),$$
and the number of calls of the \(({{\delta }_{g}},{{L}_{g}},{{\mu }_{g}})\)-gradient \({{\nabla }_{{{{\delta }_{g}}}}}g(x)\) is
$$k \times T = O\left( {\sqrt {\frac{{{{L}_{r}} + {{\mu }_{g}}}}{\mu }} \log\frac{1}{\varepsilon }} \right) \times O\left( {\sqrt {\frac{{{{L}_{r}} + {{L}_{g}}}}{{{{L}_{r}} + {{\mu }_{g}}}}} \log\frac{{{{L}_{r}} + {{L}_{g}}}}{{\delta ({{L}_{r}} + {{\mu }_{g}})}}} \right) = \tilde {O}\left( {\sqrt {\frac{{{{L}_{r}} + {{L}_{g}}}}{\mu }} \log\frac{1}{\varepsilon }} \right) = \tilde {O}\left( {\sqrt {\frac{{{{L}_{g}} + {{\mu }_{r}}}}{\mu }} \log\frac{1}{\varepsilon }} \right)$$
due to the assumption \({{L}_{r}} \leqslant {{L}_{g}}\) (this assumption is not essential due to the symmetry of the estimates found for \({{\delta }_{r}}\) and \({{\delta }_{g}}\)).