Skip to main content
SpringerLink
Log in

Tuned Liquid Column for Dampering Rotational Motion of a Nonlinear Horizontal Deck

  • Original Paper
  • Published:
Journal of Vibration Engineering & Technologies Aims and scope Submit manuscript

Abstract

Purpose and Background

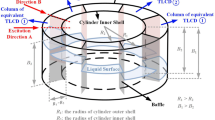
This paper aims to show how we can reduce rotational motions of a rigid mechanical structure subjected to a harmonic excitation using a tuned liquid column damper (TLCD). The studied mechanical structure here is a nonlinear horizontal deck regularly found in on/offshore. In civil and mechanical engineering, structures could be subjected to various types of external excitations leading to undesirable high amplitude of vibration.

Methods

This paper presents the modeling of a nonlinear horizontal deck with a TLCD and how it can be arranged to mitigate the vibrations. The Routh–Hurwitz criterion is used to derive the stability condition of the controlled system.

Results

The stability domain is displayed in the function of coupling parameters between the structure and the TLCD.

Conclusion

Some physical parameters of the TLCD such as the head loss coefficient δ, the horizontal length Lh and the crosssection ratio ν are optimized in order to the reduce considerably vibration amplitude of the mechanical structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Xue SD, Ko JM, Xu YL (2000) Tuned liquid column damper for suppressing pitching motion of structures. Eng Struct 23(11):1538–51

    Article  Google Scholar 

  2. Iyengar RN, Shinozuk M (1972) Effect of self-weight and vertical acceleration on the behaviour of tall structures during earthquake. Earthq Eng Struct Dyn 1:69–78

    Article  Google Scholar 

  3. Dorka UE (2014) Seismic control for elevated roads. Build Mater Struct 57:9–20

    Google Scholar 

  4. Fankem ER, Nana Nbendjo BR, Woafo P, Dorka U (2020) An inverted pendulum with multi-branching view as self-controlled system: modelling and vibration absorber capacity. J Vib Control 26(19–20):1848–1858

    Article  MathSciNet  Google Scholar 

  5. McNamara JR (1977) Tuned mass dampers for buildings. J Struct Eng ASCE 103(ST9):1785–1798

    Google Scholar 

  6. Manchalwar A, Bakre SV (2020) Vibration control of structure by top base isolated storey as tuned mass damper. Int J Dyn Control 8:963972

    Google Scholar 

  7. Soltani P, Deraemaeker P (2021) Pendulum tuned mass dampers and tuned mass dampers: analogy and optimum parameters for various combinations of response and excitation parameters. J Vibr Control 0(0):116

  8. Fujino Y, Sun L, Pacheco BM, Chaiseri P (1992) Tuned liquid damper (TLD) for suppressing horizontal motion of structures. J Eng Mech ASCE 118(10):2017–2030

    Article  Google Scholar 

  9. Sakai F, Takaeda S, Tamaki T (1989) Tuned liquid column damper - new type device for suppression of building vibration. Proc. Int. Conf. on High-rise Buildings. Nanjing, China, pp 926–931

    Google Scholar 

  10. Wu JC, Shih MH, Lin YY, Shen YC (2005) Design guidelines for tuned liquid column damper for structures responding to wind. Eng Struct 27(13):1893–1905

    Article  Google Scholar 

  11. Ahadi P, Mohebbi M, Shakeri K (2012) Using optimal multiple tuned liquid column dampers for mitigating the seismic response of structures. ISRN Civil Eng 2012:1–6

    Article  Google Scholar 

  12. Hassani S, Majid A (2016) Optimisation of pendulum liquid column damper in tall building under horizontal earthquake excitation. Royal society of sciences 85:514–531

    Google Scholar 

  13. Chang CC, Hsu CT (1998) Control performance of liquid column vibration absorbers. Eng Struct 20(7):580–586

    Article  Google Scholar 

  14. Balendra T, Wang CM, Rakesh G (1999) Effectiveness of TLCD on various structural systems. Eng Struct 21(4):291–305

    Article  Google Scholar 

  15. Xu YL, Samali B, Kwok KCS (1992) Control of along-wind response of structures by mass and liquid dampers. ASCE J Eng Mech 118(1):20–39

    Article  Google Scholar 

  16. Hitchcock PA, Kwok KCS, Watkins RD (1997) Characteristics of liquid column vibration absorbers (LCVA) - I, II. Eng Struct 19:126–144

    Article  Google Scholar 

  17. Gao H, Kwok KCS, Samali B (1997) Optimization of tuned liquid column damper. Eng Struct 19(6):476–486

    Article  Google Scholar 

  18. Chang CC (1999) Mass dampers and their optimal designs for building vibration control. Eng Struct 21:454–463

    Article  Google Scholar 

  19. Farshidianfar A, Oliazadeh P, Farivar HR (2009) Optimal parameter’s design in tuned liquid column damper, 17th. Annual (International) Conference on Mechanical Engineering. University of Tehran, Iran- ISME 1-8

  20. Rozas LT, Boroschek RK, Tamburrino AT, Rojas ML (2015) A bidirectional tuned liquid column damper for reducing the seismic response of buildings. Struct Control Health Monit 1–12

  21. Zeng X, Yu Y, Liang Z, Qingquan L, Wu H (2014) A new energy-absorbing device for motion suppression in deep-sea ploating platforms. Inst Mech Chin Acad Sci 8:111–32

    Google Scholar 

  22. Espinoza G, Carrillo C, Suazo A (2018) Analysis of tuned liquid colomn damper in nonlinear structures subjected to seismic excitations. Latin Am J Solids Struct 15:1–19

    Article  Google Scholar 

  23. Feulefack Songong E, Nanha Djanan AA, Nana Nbendjo BR (2021) Vibration absorption of a rectangular plate supporting a DC motor with a TLCD. Nonlinear Dyn 105:1357–1372

    Article  Google Scholar 

  24. Wu JC, Wang YP, Lee CL, Liao PH, Chen YH (2008) Wind-induced interaction of a non-uniform tuned liquid column damper and a structure in pitching motion. Eng Struct 30:3555–65

    Article  Google Scholar 

  25. Edgardo LC, Armando MC, Héctor MC (2020) Taylor’s formula, Limited development of power series: a study of knowledge of university professors in training. Int Electron J Math Educ 15(3):1–15

    Google Scholar 

  26. De Lagrange JL (1853) Mécanique analytique. vol. 1. Mallet-Bachelier

  27. Xue SD, Ko JM, Xu YL (2002) Wind-induced vibration control of brigdes using liquid column damper. Earthq Eng Eng Vib 1(2):271–280

    Article  Google Scholar 

  28. Taflanidis AA, Angelides DC, Manos GC (2005) Optimal design and performance of liquid column mass dampers for rotational vibration control of structures under white noise excitation. Eng Struct 27(4):524–534

    Article  Google Scholar 

  29. Wiggins S (1990) Introduction to applied nonlinear dynamical systems and chaos. Springer, NewYork

    Book  MATH  Google Scholar 

  30. Mickens ER (2010) Truly nonlinear oscillations: harmonic balance, parameter expansions, iteration, and averaging methods. World Sci

  31. Cortell R (1993) Application of the fourth-order runge-kutta method for the solution of high-order general initial value problems. Comp struct 49(5):897–900

    Article  MathSciNet  MATH  Google Scholar 

  32. Wu JC, Chang CH, Lin YY (2009) Optimal designs for non-uniform tuned liquid column damprs in horizontal motion. J Sound Vib Elsevier 326:104–122

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratory of Modelling and Simulation in Engineering, Biomimetics and Prototypes, Faculty of Science, University of Yaounde I, P.O. Box 812, Yaounde, Cameroon

    M. S. Kana Nguemo, A. M. Ngounou, S. C. Mba Feulefack, A. A. Nanha Djanan & B. R. Nana Nbendjo

  2. Universidade Tecnologica Federal do Parana, UTFPR, Av. Alberto Carazzai 1640, 86300-000, Cornelio Procopio, PR, Brazil

    Alessandro N. Vargas

Authors
  1. M. S. Kana Nguemo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. M. Ngounou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. C. Mba Feulefack
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. A. A. Nanha Djanan
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Alessandro N. Vargas
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. B. R. Nana Nbendjo
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. A. Nanha Djanan.

Ethics declarations

Conflict of interest

On behalf of all authors, the corresponding author states that there is no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

The fourth order Runge Kutta method was used to solve Eq.(21). The discretization and solution procedure used are given in the following link: https://docs.google.com/document/d/1p-EyGUEqWPgofZ2lwPSDuxBK_aYMmeKz/edit?usp=sharing &ouid=111563002132316730422 &rtpof=true &sd=true.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Nguemo, M.S.K., Ngounou, A.M., Feulefack, S.C.M. et al. Tuned Liquid Column for Dampering Rotational Motion of a Nonlinear Horizontal Deck. J. Vib. Eng. Technol. 11, 589–597 (2023). https://doi.org/10.1007/s42417-022-00596-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s42417-022-00596-8

Keywords

Search

Navigation