Skip to main content
SpringerLink
Log in

Observer-based Versus Non-observer Based Adaptive Control of Electrically Driven Cooperative Manipulators Using q-analogue of the Bernstein-Schurer-Stancu Operator as Uncertainty Approximator

  • Regular Papers
  • Robot and Applications
  • Published:
International Journal of Control, Automation and Systems Aims and scope Submit manuscript

    We’re sorry, something doesn't seem to be working properly.

    Please try refreshing the page. If that doesn't work, please contact support so we can address the problem.

Abstract

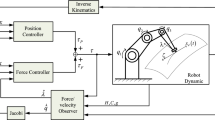
In this paper, the q-analogue of the Bernstein-Schurer-Stancu operator is proposed for uncertainty approximation in adaptive control of cooperative electrically driven manipulators. Thanks to the simplicity of the q-analogue of the Bernstein-Schurer-Stancu operator in comparison with other alternatives, the number of signals needed in the construction of the regressor vector for uncertainty approximation is reduced considerably. Studying the accuracy of model-free observers on cooperative robot manipulators is one of the motivations of this paper. Therefore, it is assumed that velocity signals are unavailable, and an observer is needed to estimate these signals. The results are also compared with the case in which velocity signals are in hand. According to the simulation result, the proposed observer can produce results that are very close to the point in which the velocity signal is used in the control law.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. Subbarao, A. Verma, and J. L. Junkins, “Model reference adaptive control of constrained cooperative manipulators,” Proc. of IEEE International Conference on Control Applications (CCA’01), pp. 553–558, 2001.

  2. B. Hu, Z. H. Guan, F. L. Lewis, and C. P. Chen, “Adaptive tracking control of cooperative robot manipulators with markovian switched couplings,” IEEE Transactions on Industrial Electronics, vol. 68, no. 3, pp. 2427–2436, 2020.

    Article  Google Scholar 

  3. M. Zribi and S. Ahmad, “Adaptive control for multiple cooperative robot arms,” Proc. of the 31st IEEE Conference on Decision and Control, pp. 1392–1398, 1992.

  4. A. Marino, “Distributed adaptive control of networked cooperative mobile manipulators,” IEEE Transactions on Control Systems Technology, vol. 26, no. 5, pp. 1646–1660, 2017.

    Article  Google Scholar 

  5. Z. Peng, D. Wang, H. Zhang, G. Sun, and H. Wang, “Distributed model reference adaptive control for cooperative tracking of uncertain dynamical multi-agent systems,” IET Control Theory & Applications, vol. 7, no. 8, pp. 1079–1087, 2013.

    Article  MathSciNet  Google Scholar 

  6. C. K. Verginis, M. Mastellaro, and D. V. Dimarogonas, “Robust cooperative manipulation without force/torque measurements: Control design and experiments,” IEEE Transactions on Control Systems Technology, vol. 28, no. 3, pp. 713–729, 2019.

    Article  Google Scholar 

  7. F. Abdelhedi, Y. Bouteraa, and N. Derbel, “Second order sliding mode-based synchronization control for cooperative robot manipulators,” Advances and Applications in Nonlinear Control Systems, pp. 669–683, 2016.

  8. Y. Liu, C. He, and S. Cheng, “Adaptive fuzzy sliding mode control for collaborative robot based on nominal model,” Proc. of 6th International Conference on Control, Robotics and Cybernetics (CRC), pp. 41–46, 2021.

  9. M. Farahmandrad, S. Ganjefar, H. A. Talebi, and M. Bayati, “Fuzzy sliding mode controller design for a cooperative robotic system with uncertainty for handling an object,” Journal of Dynamic Systems, Measurement, and Control, vol. 141, no. 6, 061010, 2019.

    Article  Google Scholar 

  10. W. Gueaieb, S. Al-Sharhan, and M. Bolic, “Robust computationally efficient control of cooperative closed-chain manipulators with uncertain dynamics,” Automatica, vol. 43, no. 5, pp. 842–851, 2007.

    Article  MathSciNet  MATH  Google Scholar 

  11. D. Zhao, C. Li, and Q. Zhu, “Low-pass-filter-based position synchronization sliding mode control for multiple robotic manipulator systems,” Proc. of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, vol. 225, no. 8, pp. 1136–1148, 2011.

    Google Scholar 

  12. D. Zhao and Q. Zhu, “Position synchronised control of multiple robotic manipulators based on integral sliding mode,” International Journal of Systems Science, vol. 45, no. 3, pp. 556–570, 2014.

    Article  MathSciNet  MATH  Google Scholar 

  13. H. N. Thai, A. T. Phan, C. K. Nguyen, Q. U. Ngo, P. T. Dinh, and Q. T. Vo, “Trajectory tracking control design for dual-arm robots using dynamic surface controller,” Proc. of International Symposium on Instrumentation, Control, Artificial Intelligence, and Robotics (ICA-SYMP), pp. 115–118, 2019.

  14. G. P. Incremona, De G. Felici, A. Ferrara, and E. Bassi, “A supervisory sliding mode control approach for cooperative robotic system of systems,” IEEE Systems Journal, vol. 9, no. 1, pp. 263–272, 2013.

    Article  Google Scholar 

  15. M. Azadi and M. Eghtesad, “An adaptive-robust control approach for trajectory tracking of two 5 DOF cooperating robot manipulators moving a rigid payload,” AUT Journal of Modeling and Simulation, vol. 41, no. 1, pp. 1–9, 2009.

    Google Scholar 

  16. M. Deghat, A. R. Khayatian, and M. Eghtesad, “Experimental study of a robust-adaptive controller design for two cooperating RLED robot manipulators carrying a rigid payload,” Proc. of IEEE International Conference on Mechatronics, pp. 1–6, 2009.

  17. A. Zhai, J. Wang, H. Zhang, G. Lu, and H. Li, “Adaptive robust synchronized control for cooperative robotic manipulators with uncertain base coordinate system,” ISA Transactions, vol. 126, pp. 134–143., 2022.

    Article  Google Scholar 

  18. R. Mohajerpoor, M. Rezaei, A. Talebi, M. Noorhosseini, and R. Monfaredi, “Robust adaptive hybrid force/position control scheme of two planar manipulators handling an unknown object interacting with an environment,” Proc. of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, vol. 226, no. 4, pp. 509–522, 2012.

    Google Scholar 

  19. K. Bai, M. Luo, M. Liu, and G. Jiang, “Fuzzy backstepping control for dual-arm cooperative robot grasp,” IEEE International Conference on Robotics and Biomimetics (RO-BIO), pp. 2563–2568, 2015.

  20. K. Y. Lian, C. S. Chiu, and P. Liu, “Semi-decentralized adaptive fuzzy control for cooperative multirobot systems with h/sup/splinfin//motion/internal force tracking performance,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 32, no. 3, pp. 269–280, 2002.

    Article  Google Scholar 

  21. G. Enthrakandi Narasimhan and J. Bettyjane, “Implementation and study of a novel approach to control adaptive cooperative robot using fuzzy rules,” International Journal of Information Technology, vol. 13, no. 6, pp. 2287–2294, 2021.

    Article  Google Scholar 

  22. A. Zhai, H. Zhang, J. Wang, G. Lu, J. Li, and S. Chen, “Adaptive neural synchronized impedance control for cooperative manipulators processing under uncertain environments,” Robotics and Computer-Integrated Manufacturing, vol. 75, 102291, 2022.

    Article  Google Scholar 

  23. M. Hanafusa and J. Ishikawa, “Mechanical impedance control of cooperative robot during object manipulation based on external force estimation using recurrent neural network,” Unmanned Systems, vol. 8, no. 3, pp. 239–251, 2020.

    Article  Google Scholar 

  24. P. Esmaili and H. Haron, “Adaptive synchronous artificial neural network-based PI-type sliding mode control on two robot manipulators,” Proc. of International Conference on Computer, Communications, and Control Technology, pp. 515–519, 2015.

  25. M. Li, H. Chen, and R. Zhang, “An input dead zones considered adaptive fuzzy control approach for double pendulum cranes with variable rope lengths,” IEEE/ASME Transactions on Mechatronics, vol. 27, no. 5, pp. 3385–3396, 2022.

    Article  Google Scholar 

  26. A. Izadbakhsh, “FAT-based robust adaptive control of electrically driven robots without velocity measurements,” Nonlinear Dynamics, vol. 89, no. 1, pp. 289–304, 2017.

    Article  MathSciNet  MATH  Google Scholar 

  27. A. Izadbakhsh, I. Zamani, and S. Khorashadizadeh, “Szász-Mirakyan-based adaptive controller design for chaotic synchronization,” International Journal of Robust and Nonlinear Control, vol. 31, no. 5, pp. 1689–1703, 2021.

    Article  MathSciNet  Google Scholar 

  28. A. Izadbakhsh, “Robust control design for rigid-link flexible-joint electrically driven robot subjected to constraint: Theory and experimental verification,” Nonlinear Dynamics, vol. 85, no. 2, pp. 751–765, 2016.

    Article  MathSciNet  MATH  Google Scholar 

  29. A. Izadbakhsh and N. Nikdel, “Chaos synchronization using differential equations as extended state observer,” Chaos, Solitons & Fractals, vol. 153, 111433, 2021.

    Article  MathSciNet  MATH  Google Scholar 

  30. A. Izadbakhsh and N. Nikdel, “Robust adaptive controller-observer scheme for robot manipulators: A Bern-stein-Stancu approach,” Robotica, vol. 40, no. 5, pp. 1309–1325, 2022.

    Article  Google Scholar 

  31. S. Khorashadizadeh and M. Sadeghijaleh, “Adaptive fuzzy tracking control of robot manipulators actuated by permanent magnet synchronous motors,” Computers & Electrical Engineering, vol. 72, pp. 100–111, 2018.

    Article  Google Scholar 

  32. N. Sadati and E. Elhamifar, “Robust decentralized position/force control of cooperative robots without velocity measurement,” Proc. of IEEE International Conference on Industrial Technology, pp. 1403–1408, 2005.

  33. W. He, Y. Sun, Z. Yan, C. Yang, Z. Li, and O. Kay-nak, “Disturbance observer-based neural network control of cooperative multiple manipulators with input saturation,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 5, pp. 1735–1746, 2019.

    Article  MathSciNet  Google Scholar 

  34. S. Yousefizadeh and T. Bak, “Nonlinear disturbance observer for external force estimation in a cooperative robot,” Proc. of 19th International Conference on Advanced Robotics, pp. 220–226, 2019.

  35. K. D. Kallu, W. Jie, and M. C. Lee, “Sensorless reaction force estimation of the end effector of a dual-arm robot manipulator using sliding mode control with a sliding perturbation observer,” International Journal of Control, Automation, and Systems, vol. 16, no. 3, pp. 1367–1378, 2018.

    Article  Google Scholar 

  36. H. H. Kim, M. C. Lee, J. H. Kyung, and H. M. Do, “Evaluation of force estimation method based on sliding perturbation observer for dual-arm robot system,” International Journal of Control, Automation, and Systems, vol. 19, no. 1, pp. 1–10, 2021.

    Article  Google Scholar 

  37. N. Sadati and E. Elhamifar, “Output feedback adaptive decentralized control of cooperative robots”, Proc. of International Conference on Industrial Electronics and Control Applications, pp. 6, 2005.

  38. V. Parra-Vega, “On the control of cooperative robots without velocity measurements,” IEEE Transactions on Control Systems Technology, vol. 12, no. 4, pp. 600–608, 2004.

    Article  Google Scholar 

  39. J. C. Martínez-Rosas, M. A. Arteaga, and A. M. Castillo-Sánchez, “Decentralized control of cooperative robots without velocity–force measurements,” Automatica, vol. 42, no. 2, pp. 329–336, 2006.

    Article  MathSciNet  MATH  Google Scholar 

  40. P. N. Agrawal, V. Gupta, and A. Sathish Kumar, “On q-analogue of Bernstein-Schurer-Stancu operators,” Applied Mathematics and Computation, vol. 219, pp. 7754–7764, 2013.

    Article  MathSciNet  MATH  Google Scholar 

  41. A. Deylami and A. Izadbakhsh, “Brenke-type polynomials-based robust adaptive control of cooperative multiple manipulators without velocity measurements,” International Journal of Control, pp. 1–14, 2022. DOI: https://doi.org/10.1080/00207179.2022.2146604

  42. A.-C. Huang and M.-C. Chien, “A unified regressor - Free approach,” Adaptive Control of Robot Manipulators, World Scientific, 2010.

Download references

Author information

Authors and Affiliations

  1. Department of Electrical Engineering, Garmsar Branch, Islamic Azad University, Garmsar, Iran

    Alireza Izadbakhsh & Ali Deylami

  2. Faculty of Electrical and Computer Engineering, University of Birjand, Birjand, 97175/615, Iran

    Saeed Khorashadizadeh

Authors
  1. Alireza Izadbakhsh
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ali Deylami
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Saeed Khorashadizadeh
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Izadbakhsh.

Additional information

Publisher’s Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Alireza Izadbakhsh received his B.S. degree in electrical engineering from the Islamic Azad University, Garmsar Branch, Garmsar, Iran, in 2003, his M.Sc. and Ph.D. degrees from the Shahrood University of Technology, Shahrood, Iran, in 2007 and 2013, respectively, all in control engineering. His research interests include robust/adaptive control of nonlinear systems and function approximation theory.

Ali Deylami received his B.S. and M.Sc. degrees in electrical engineering, both from the Islamic Azad University, Mah-mudabad Branch, in 2015, and 2017, respectively. His research interests include nonlinear control, adaptive control, and robot control.

Saeed Khorashadizadeh was born in Mashhad, Iran. He studied at Ferdowsi University of Mashhad and received his B.S. degree in electrical engineering in 2009. Then he moved to Shahrood and received his M.S. and Ph.D. degrees in control engineering from Shahrood University of Technology, in 2011 and 2015, respectively. Now, he is an assistant professor in University of Birjand, Iran. His research interests include control, dynamical systems, robotics, and artificial intelligence.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Izadbakhsh, A., Deylami, A. & Khorashadizadeh, S. Observer-based Versus Non-observer Based Adaptive Control of Electrically Driven Cooperative Manipulators Using q-analogue of the Bernstein-Schurer-Stancu Operator as Uncertainty Approximator. Int. J. Control Autom. Syst. 21, 2664–2673 (2023). https://doi.org/10.1007/s12555-022-0592-8

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12555-022-0592-8

Keywords

Search

Navigation