Off-shell T-matrix for the Manning–Rosen potential

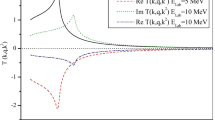
Abstract

New analytical expressions for the off-shell wave functions and T-matrix with the Manning–Rosen potential are constructed in terms of generalised hypergeometric functions. The off-shell T-matrices are computed for the neutron–proton and neutron–deuteron systems. The limiting behaviours of our expression for the off-shell T-matrix are verified and found correct.

Appendix A

The Manning–Rosen potential

$$\begin{aligned} V_{\mathrm{MR}} (r)=\frac{1}{b^{2}}\left\{ {\frac{\alpha \left( {\alpha -1} \right) \text{ e}^{-2r/b}}{\left( {1-\text{ e}^{-r/b}} \right) ^{2}}-\frac{A\text{ e}^{-r/b}}{\left( {1-\text{ e}^{-r/b}} \right) }} \right\} \nonumber \\ \end{aligned}$$

(A1)

converts into the Hulthén potential when $\alpha =0$ and reads as

$$\begin{aligned} V_{\mathrm{H}} (r)=V_{0} \frac{\text{ e}^{-r/b}}{\left( {1-\text{ e}^{-r/b}} \right) }\,;\,\,\,\,\,\,\,V_{0} =-A/b^{2}. \end{aligned}$$

(A2)

Under the limit eq. (27) leads to

$$\begin{aligned}&T_{1} (q,p,k^{2})=b^{3}\sum \limits _{n=0}^\infty \frac{\Gamma (n+1-i\,(k-p)b)\Gamma (-i\,(k+q)b)\Gamma (n+2)}{\Gamma (1-i\,(k-p)b)\Gamma (n+2-i\,(k+q)b)\Gamma (n+1)\,} \nonumber \\&\quad \qquad \qquad \qquad \times { }_{3}F_{2} \left( {1,1+n+X,1+n+Y;\,2+n,\,3+n-ib\left( {k+p} \right) ;1} \right) \nonumber \\&\quad \qquad \qquad \qquad -\frac{b^{2}\Gamma (-i\,(k+q)b)\Gamma (i\,(k-q)b)}{f_{\mathrm{H}} (k)i(k+p)\Gamma (1+i\,(k-q)b+X)\Gamma (1+i\,(k-q)b+Y)} \nonumber \\&\quad \qquad \qquad \qquad \times {}_{3}F_{2} \left( {X,\,Y,\,-i\,(k+p)b;\,1-2ikb,\,1-i\,(k+p)b;\,1} \right) \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$

(A3)

with

$$\begin{aligned} X= & {} 1-ikb+ib\left( {k^{2}+V_{0} } \right) ^{1/2}\nonumber \\ \hbox { and }\, \nonumber \\ Y= & {} 1-ikb-ib\left( {k^{2}+V_{0}} \right) ^{1/2}. \end{aligned}$$

(A4)

Using the following relations of $f_{n} \left( {a\,,\,b\,;\,c\,;z} \right)$ and ${ }_{3}F { }_{2}$(*) functions [33, 44]

$$\begin{aligned}&f_{n} \left( {a\,,\,b\,;\,c\,;z} \right) \,=\frac{z^{n}}{n(n\,+\,c\,-1)}\,\nonumber \\&\quad \times _{3}F_{2}\left( {1,\,n\,+\,a,\,n\,+\,b;n\,+\,1,\,n\,+c\,;\,z\,} \right) , \end{aligned}$$

(A5)

$$\begin{aligned}&f_{m} \left( {a,\,b;\,c;\,z} \right) =\frac{\Gamma (m)\Gamma (m+c-1)\Gamma (a)\Gamma (b)}{\Gamma (m+a)\Gamma (m+b)\Gamma (c)}\nonumber \\&\quad \times \sum \limits _{i=0}^\infty \frac{\Gamma (m+i+a)\Gamma (m+a+b)\Gamma (c)\,z^{m+i}}{\Gamma (a)\Gamma (b)\Gamma (m+i+c)\Gamma (m+i+1)}; \nonumber \\&\quad m\,\rightarrow \text{ positive } \text{ integer }\,\text{, } \end{aligned}$$

(A6)

$$\begin{aligned}&{ }_{3}F{ }_{2}\left( {\alpha ,\,\beta ,\,\,\gamma ;\, \delta ,\,\varepsilon ;\,\,1} \right) \nonumber \\&\quad =\frac{\Gamma (\varepsilon ) \Gamma (\delta +\varepsilon -\alpha -\beta -\gamma )}{\Gamma (\varepsilon -\gamma )\Gamma (\delta +\varepsilon -\alpha -\beta )}\nonumber \\&\qquad \times _{3}F{ }_{2}\left( {\delta {-}\alpha ,\,-\beta ,\,\gamma ;\,\delta ,\,\varepsilon {+}\delta {-}\alpha {-}\beta ;\,\,1} \right) , \end{aligned}$$

(A7)

$$\begin{aligned}&{ }_{3}F{ }_{2}\left( {a,\,b,\,c;\,e,\,f;\,\,1} \right) \nonumber \\&\quad =\frac{\Gamma (s)\Gamma (f)}{\Gamma (f-a)\Gamma (s+a)}\nonumber \\&\qquad \times {}_{3}F{ }_{2} \left( {a,\,e-b,\,e-c;\,e,\,s+a;\,\,1} \right) ; \nonumber \\&s=e+f-a-b-c \end{aligned}$$

(A8)

and

$$\begin{aligned}&\sum \limits _{L=0}^n \frac{(a)_{L} \,(b)_{L} }{(c)_{L} \,\Gamma (L+1)} =\frac{\Gamma (a+n+1)\Gamma (b+n+1)}{\Gamma (a+b+n+1)\Gamma (n+1)}\nonumber \\&\quad \times {}_{3}F{ }_{2}\left( a,\,b,\,\,c+n;\,c,\,a +b+n+1;\,\,1 \right) \end{aligned}$$

(A9)

in eq. (A3) one gets

$$\begin{aligned}&T_{1} (q,p,k^{2})= -b^{3}\sum \limits _{n=0}^\infty {\frac{\Gamma (Y+1)\Gamma (-i\,(k+q)b)}{(X+1)\Gamma (1-i\,(k-p)b)\Gamma (2-i\,(k+q)b)\,}} \nonumber \\&\times \sum \limits _{n=0}^\infty {\frac{(n+1)\Gamma (n+1-\,i\,(k-p)b)}{\Gamma (n+Y+2)}} { }_{3} F_{2} \left( -n,\,X+1,\,\,1-i\,(k+q)b-Y;\,X+2,\,2-i\,(k+q)b;\,1 \right) .\nonumber \\ \end{aligned}$$

(A10)

Expanding the sum, rearranging the terms along with eq. (32) we finally obtain

$$\begin{aligned}&T_{1} (q,p,k^{2})=-b^{3} \nonumber \\&\times \frac{Y\,\Gamma (Y+i(k-p)b-1)\Gamma (-i\,(k+q)b)}{(X+1)\Gamma (Y+1+i\,(k-p)b)\Gamma (2-i\,(k+q)b)\,} \nonumber \\&\times { }_{4}F_{3} \left( 2,\,X+1,\,\,1-i\,(k-p)b,\,1-i\,(k+q)b-Y;\right. \nonumber \\&\quad \left. \,X+2,\,2-i\, (k+q)b,\,2-Y\right. \nonumber \\&\quad \left. -i\,(k-p)b;\,1\right) . \end{aligned}$$

(A11)

Therefore, eq. (24) together with eq. (A11) produce the Hulthén off-shell T-matrix [17].