Mathematical Modeling to Guide Experimental Design: T Cell Clustering as a Case Study

Abstract

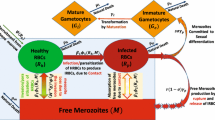
Mathematical modeling provides a rigorous way to quantify immunological processes and discriminate between alternative mechanisms driving specific biological phenomena. It is typical that mathematical models of immunological phenomena are developed by modelers to explain specific sets of experimental data after the data have been collected by experimental collaborators. Whether the available data are sufficient to accurately estimate model parameters or to discriminate between alternative models is not typically investigated. While previously collected data may be sufficient to guide development of alternative models and help estimating model parameters, such data often do not allow to discriminate between alternative models. As a case study, we develop a series of power analyses to determine optimal sample sizes that allow for accurate estimation of model parameters and for discrimination between alternative models describing clustering of CD8 T cells around Plasmodium liver stages. In our typical experiments, mice are infected intravenously with Plasmodium sporozoites that invade hepatocytes (liver cells), and then activated CD8 T cells are transferred into the infected mice. The number of T cells found in the vicinity of individual infected hepatocytes at different times after T cell transfer is counted using intravital microscopy. We previously developed a series of mathematical models aimed to explain highly variable number of T cells per parasite; one of such models, the density-dependent recruitment (DDR) model, fitted the data from preliminary experiments better than the alternative models, such as the density-independent exit (DIE) model. Here, we show that the ability to discriminate between these alternative models depends on the number of parasites imaged in the analysis; analysis of about $n=50$ parasites at 2, 4, and 8 h after T cell transfer will allow for over 95% probability to select the correct model. The type of data collected also has an impact; following T cell clustering around individual parasites over time (called as longitudinal (LT) data) allows for a more precise and less biased estimates of the parameters of the DDR model than that generated from a more traditional way of imaging individual parasites in different liver areas/mice (cross-sectional (CS) data). However, LT imaging comes at a cost of a need to keep the mice alive under the microscope for hours which may be ethically unacceptable. We finally show that the number of time points at which the measurements are taken also impacts the precision of estimation of DDR model parameters; in particular, measuring T cell clustering at one time point does not allow accurately estimating all parameters of the DDR model. Using our case study, we propose a general framework on how mathematical modeling can be used to guide experimental designs and power analyses of complex biological processes.