Skip to main content
SpringerLink
Log in

Solving Inventory Management Problems through Deep Reinforcement Learning

  • Published:
Journal of Systems Science and Systems Engineering Aims and scope Submit manuscript

Abstract

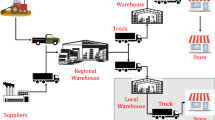
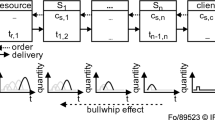
Inventory management (e.g. lost sales) is a central problem in supply chain management. Lost sales inventory systems with lead times and complex cost function are notoriously hard to optimize. Deep reinforcement learning (DRL) methods can learn optimal decisions based on trails and errors from the environment due to its powerful complex function representation capability and has recently shown remarkable successes in solving challenging sequential decision-making problems. This paper studies typical lost sales and multi-echelon inventory systems. We first formulate inventory management problem as a Markov Decision Process by taking into account ordering cost, holding cost, fixed cost and lost-sales cost and then develop a solution framework DDLS based on Double deep Q-networks (DQN).

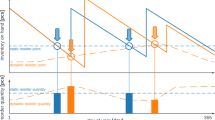
In the lost-sales scenario, numerical experiments demonstrate that increasing fixed ordering cost distorts the ordering behavior, while our DQN solutions with improved state space are flexible in the face of different cost parameter settings, which traditional heuristics find challenging to handle. We then study the effectiveness of our approach in multi-echelon scenarios. Empirical results demonstrate that parameter sharing can significantly improve the performance of DRL. As a form of information sharing, parameter sharing among multi-echelon suppliers promotes the collaboration of agents and improves the decision-making efficiency. Our research further demonstrates the potential of DRL in solving complex inventory management problems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Data Availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

  • Angulo A, Nachtmann H, Waller M A (2011). Supply chain information sharing in a vendor managed inventory partnership. Journal of Business Logistics 25(1): 101–120.

    Article  Google Scholar 

  • Arrow K J, Karlin S, Scarf H E. (1958). Studies in the Mathematical Theory of Inventory and Production. Stanford University.

  • Arulkumaran K, Deisenroth M P, Brundage M, Bharath A A (2017). Deep reinforcement learning: A brief survey. IEEE Signal Processing Magazine 34(6): 26–38.

    Article  Google Scholar 

  • Beamon B M (1998). Supply chain design and analysis: Models and methods. International Journal of Production Economics 55(3): 281–294.

    Article  Google Scholar 

  • Bijvank M, Vis I F A (2011). Lost-sales inventory theory: A review. European Journal of Operational Research 215(1): 1–13.

    Article  MathSciNet  MATH  Google Scholar 

  • Chen F, Drezner Z, Ryan J K, Simchi-Levi D (2000). Quantifying the bullwhip effect in a simple supply chain: The impact of forecasting, lead times, and information. Management Science 46(3): 436–443.

    Article  MATH  Google Scholar 

  • Chi C (2006). Optimal ordering policies for periodic-review systems with replenishment cycles. European Journal of Operational Research 170(1): 44–56.

    Article  MathSciNet  MATH  Google Scholar 

  • Federgruen A, Zipkin P H (1984). An efficient algorithm for computing optimal (s, S) policies. Operations Research 32(6): 1268–1285.

    Article  MathSciNet  MATH  Google Scholar 

  • Feldman, Richard M (1978). A continuous review (s, S) inventory system in a random environment. Journal of Applied Probability 15(3): 654–659.

    Article  MathSciNet  MATH  Google Scholar 

  • Gijsbrechts J, Boute R N, Van Mieghem J, Zhang D (2021). Can deep reinforcement learning improve inventory management? Performance on dual sourcing, lost sales and multi-echelon problems. Manufacturing and Service Operations Management 24: 1349–1368.

    Article  Google Scholar 

  • Goldberg D A, Katz-Rogozhnikov D A, Lu Y, Sharma M, Squillante M S (2012). Asymptotic optimality of constant-order policies for lost sales inventory models with large lead times. Mathematics of Operations Research 41(3): 898–913.

    Article  MathSciNet  MATH  Google Scholar 

  • Huh W T, Janakiraman G, Muckstadt J A, Rusmevichientong P (2009). Asymptotic optimality of Order-Up-To policies in lost sales inventory systems. Management Science 55(3): 404–420.

    Article  MATH  Google Scholar 

  • Ivanov S, D’yakonov A (2019). Modern deep reinforcement learning algorithms. arXiv Preprint arXiv:1906.10025.

  • Johnson E L (1968). On (s, S) policies. Management Science 15(1): 80–101.

    Article  MATH  Google Scholar 

  • Karlin S, Scarf H. (1958). Inventory models of the Arrow-Harris-Marschak type with time lag. Studies in the Mathematical Theory of Inventory and Production. Palo Alto, CA: Standford University Press.

    MATH  Google Scholar 

  • Kodama, M. (1967). The optimality of (S,s) policies in the dynamic inventory problem with emergency and non-stationary stochastic demands. Kumamoto Journal of Science.ser.a Mathematics Physics & Chemistry 8(1): 1–10.

    MATH  Google Scholar 

  • Kok T D, Grob C, Laumanns M, Minner S, Rambau J, Schade K (2018). A typology and literature review on stochastic multi-echelon inventory models. European Journal of Operational Research 269(3): 955–983.

    Article  MathSciNet  MATH  Google Scholar 

  • Li Y(2017). Deep reinforcement learning: An overview. arXiv preprint arXiv:1701.07274.

  • McGrath T, Kapishnikov A, McGrath T, Kapishnikov A, Tomasev N, Pearce A, Hassabis D, Kim B, Paquet U, Kramnik V(2021). Acquisition of chess knowledge in Alphazero. arXiv preprint arXiv:2111.09259.

  • Mnih V, Kavukcuoglu K, David S, Alex G, Ioannis A, Daan W, Martin R (2013). Playing Atari with deep reinforcement learning. arXiv Preprint arXiv:1312.5602.

  • Minh V, Kavukcuoglu K, Silver D, Rusu A A, Veness J, Bellemare M G, Graves A, Riedmiller Martin, Fidjeland A K, Ostrovski G, Petersen Stig, Beattie C, Sadik A, Antonoglou I, King H, Kumaran D, Wierstra D, Legg S, Hassabis D (2015). Human-level control through deep reinforcement learning. Nature 518(7540): 529–533.

    Article  Google Scholar 

  • Mnih V, Badia A P, Mirza M, Graves A, Lillicrap T, Harley T, Silver D, Kavukcuoglu K (2016). Asynchronous methods for deep reinforcement learning. International Conference on Machine Learning 1928–1937, June, 2016.

  • Moor B, Gisbrechts J, Boute R N, Slowinski R, Artalejo J, Billaut J C, Dyson R, Peccati L (2022). Reward shaping to improve the performance of deep reinforcement learning in perishable inventory management. European Journal of Operational Research 301(2): 535–545.

    Article  Google Scholar 

  • Ruud H T, Willem K (2008). Dynamic inventory rationing strategies for inventory systems with two demand classes, Poisson demand and backordering. European Journal of Operational Research 190(1): 156–178.

    Article  MATH  Google Scholar 

  • Schulman J, Wolski F, Dhariwal P, Radford A, Klimov O (2017). Proximal policy optimization algorithms. arXiv Preprint arXiv:1707.06347.

  • Sherbrooke, Craig C (1968). Metric: A multi-echelon technique for recoverable item control. Operations Research. 16(1): 122–141.

    Article  Google Scholar 

  • Van H H, Guez A, Silver D (2016). Deep reinforcement learning with double Q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence 30, March, 2016.

  • Vanvuchelen N, Gijsbrechts, J, Boute R (2020). Use of proximal policy optimization for the joint replenishment problem. Computers in Industry 119: 103239.

    Article  Google Scholar 

  • Verhoef P C, Sloot L M (2006). Out-of-Stock: Reactions, antecedents, management solutions, and a future perspective. Retailing in the 21st Century. Springer, Berlin, Heidelberg.

    Google Scholar 

  • Watkins, Christopher John Cornish Hellaby (1989). Learning from Delayed Rewards. King’s College, Cambridge, United Kingdom.

    Google Scholar 

  • Xin L (2021). Understanding the performance of capped base-stock policies in lost-sales inventory models. Operations Research 69(1): 61–70.

    Article  MathSciNet  MATH  Google Scholar 

  • Xin L, Goldberg D A (2016). Optimality gap of constant-order policies decays exponentially in the lead time for lost sales models. Operations Research 64(6): 1556–1565.

    Article  MathSciNet  MATH  Google Scholar 

  • Zabel E (1962). A note on the optimality of (S,s) policies in inventory theory. Management Science 9(1): 123–125.

    Article  Google Scholar 

  • Zhao X, Qiu M (2007). Information sharing in a multi-echelon inventory system. Tsinghua Science & Technology. 12(4): 466–474.

    Article  MathSciNet  MATH  Google Scholar 

  • Zipkin P (2008). Old and new methods for lost-Sales inventory systems. Operations Research: The Journal of the Operations Research Society of America 56(5): 1256–1263.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work has been supported in part by (i) the National Natural Science Foundation of China, under grant Nos. 72022001, 92146003, and 71901003; (ii) CAAI-Huawei MindSpore, CCF-Tencent Open Research Fund.

Author information

Authors and Affiliations

  1. Center for Multi-Agent Research, Institute for AI, Peking University, Beijing, 100871, China

    Qinghao Wang, Yijie Peng & Yaodong Yang

  2. Guanghua School of Management, Peking University, Beijing, 100871, China

    Yijie Peng

  3. College of Engineering, Peking University, Beijing, 100871, China

    Qinghao Wang

Authors
  1. Qinghao Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yijie Peng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yaodong Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yijie Peng or Yaodong Yang.

Additional information

Qinghao Wang is a PhD student in the College of Engineering, at Peking University, Bejing, China. His research interests include multi-agent systems, deep reinforcement learning and game theory.

Yijie Peng is an associate professor in Guanghua School of Management, with affiliate faculty appointments in the Institute of Artificial Intelligence and National Institute of Health Data Science, all at Peking University. He got his PhD degree in management science from Fudan University in Shanghai, China, and B.S degree in mathematics from Wuhan University in China. His research interests include stochastic modeling and analysis, simulation optimization, machine learning, data analysis, and healthcare. He received Excellent Young Scholar Grant from NSFC, and was awarded INFORMS Outstanding Simulation Publication Award in 2019. He is a member of INFORMS and IEEE, and serves as an Associate Editor of the Asia-Pacific Journal of Operational Research and the Conference Editorial Board of the IEEE Control Systems Society.

Yaodong Yang is a machine learning researcher with ten-year working experience in both academia and industry. Currently, he is an assistant professor at Institute for AI, Peking University. His research is about reinforcement learning and multi-agent systems. He has maintained a track record of more than sixty publications at top conferences (NeurIPS, ICML, ICLR, etc) and top journals (Artificial Intelligence, National Science Review, etc), along with the best system paper award at CoRL 2020 and the best blue-sky paper award at AAMAS 2021. Before joining Peking University, he was an assistant professor at King’s College London. Before KCL, he was a principal research scientist at Huawei U.K. Before Huawei, he was a senior research manager at American International Group. He holds a Ph.D. degree from University College London, an M.Sc. degree from Imperial College London and a Bachelor degree from University of Science and Technology of China.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wang, Q., Peng, Y. & Yang, Y. Solving Inventory Management Problems through Deep Reinforcement Learning. J. Syst. Sci. Syst. Eng. 31, 677–689 (2022). https://doi.org/10.1007/s11518-022-5544-6

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11518-022-5544-6

Keywords

Search

Navigation