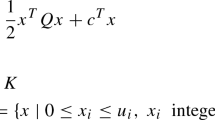Skip to main content
SpringerLink
Log in

A branch-and-cut approach to portfolio selection with marginal risk control in a linear conic programming framework

  • Published:
Journal of Systems Science and Systems Engineering Aims and scope Submit manuscript

Abstract

Marginal risk represents the risk contribution of an individual asset to the risk of the entire portfolio. In this paper, we investigate the portfolio selection problem with direct marginal risk control in a linear conic programming framework. The optimization model involved is a nonconvex quadratically constrained quadratic programming (QCQP) problem. We first transform the QCQP problem into a linear conic programming problem, and then approximate the problem by semidefinite programming (SDP) relaxation problems over some subrectangles. In order to improve the lower bounds obtained from the SDP relaxation problems, linear and quadratic polar cuts are introduced for designing a branch-and-cut algorithm, that may yield an ∈-optimal global solution (with respect to feasibility and optimality) in a finite number of iterations. By exploring the special structure of the SDP relaxation problems, an adaptive branch-and-cut rule is employed to speed up the computation. The proposed algorithm is tested and compared with a known method in the literature for portfolio selection problems with hundreds of assets and tens of marginal risk control constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Al-Khayyal, F., Larsen, C. & Van Voorhis, T. (1995). A relaxation method for nonconvex quadratically constrained quadratic programs. Journal of Global Optimization, 6: 215–230

    Article  MATH  Google Scholar 

  2. Alizadeh, F., Haeberly, J.-P. & Overton, M. (1998). Primal-dual interior-point methods for semidefinite programming: convergence rates, stability and numerical results. SIAM Journal on Optimization, 8: 746–768

    Article  MATH  MathSciNet  Google Scholar 

  3. Anstreicher, K. (2009). Semidefinite programming versus the reformulation -linearization technique for nonconvex quadratically constrained quadratic programming. Journal of Global Optimization, 43: 471–484

    Article  MATH  MathSciNet  Google Scholar 

  4. Audet, C., Hansen, P., Jaumard, B. & Savard, G. (2000). A branch and cut algorithm for non-convex quadratically constrained quadratic programming. Mathematical Programming, 87: 131–152

    MATH  MathSciNet  Google Scholar 

  5. Ben-Tal, A. & Nemirovskii, A. (2001). Lectures on Modern Convex Optimization: Analysis, Algorithms and Engineering Applications. Society for Industrial and Applied Mathematics, Philadelphia

    Book  Google Scholar 

  6. Bertsimas, D., Lauprete, G. & Samarov, A. (2004). Shortfall as a risk measure: properties, optimization and applications. Journal of Economics Dynamics and Control, 28: 1353–1381

    Article  MATH  MathSciNet  Google Scholar 

  7. Bremner, D., Fukuda, K. & Marzetta, A. (1998). Primal-dual methods for vertex and facet enumeration. Discrete and Computational Geometry, 20: 333–357

    Article  MATH  MathSciNet  Google Scholar 

  8. Burer, S. & Saxena, A. (2012). The MILP Road to MIQCP. In: Lee, J., Leyer, S. (eds.), Mixed Integer Nonlinear Programming, pp. 373–405

    Chapter  Google Scholar 

  9. Deng, Z., Fang, S.-C., Jin Q. & Xing, W. (2013). Detecting copositivity of a symmetric matrix by an adaptive ellipsoid-based approximation scheme. European Journal of Operational Research, 229: 21–28

    Article  MathSciNet  Google Scholar 

  10. Dowd, K. (1999). Beyond Value at Risk: The New Science of Risk Managemet. John Wiley & Sons, New Jersey

    Google Scholar 

  11. Fang, S.-C. & Xing, W. (2013). Linear Conic Optimization. Science Press, Beijing

    Google Scholar 

  12. Grant, M. & Boyd, S. (2013). CVX: Matlab Software for Disciplined Convex Programming, version 2.0 beta. http://cvxr.com/cvx

    Google Scholar 

  13. Grinold, R. & Kahn, R. (1999). Active Portfolio Management: A Quantitative Approach for Producing Superior Returns and Controlling Risk (2nd Edition). McGraw-Hill, New York

    Google Scholar 

  14. Guo, X., Deng, Z., Fang, S.-C. & Xing, W. (2013). Quadratic optimization over one first-order cone. To appear in: Journal of Industrial and Management Optimization

    Google Scholar 

  15. Huang, F., Sun, L. & Wang, Y. (2011). Mean-variance model based on filters of minimum spanning tree. Journal of Systems Science and Systems Engineering, 20: 495–506

    Article  Google Scholar 

  16. Kim, S. & Kojima, M. (2001). Second order cone programming relaxation of nonconvex quadratic optimization problems. Optimization Methods and Software, 15: 201–224

    Article  MATH  MathSciNet  Google Scholar 

  17. Konno, H. & Yamazaki, H. (1991). Mean-absolute deviation portfolio optimization model and its applications to Tokyo stock market. Management Science, 37: 519–531

    Article  Google Scholar 

  18. Markowitz, H. (1952). Portfolio selection. Journal of Finance, 7: 77–91

    Google Scholar 

  19. Matsui, T. (1996). NP-hardness of linear multiplicative programming and related problems. Journal of Global Optimization, 9: 113–119

    Article  MATH  MathSciNet  Google Scholar 

  20. Murty, K. & Kabadi, S. (1987). Some NP-Complete problems in quadratic and non-linear programming. Mathematical Programming, 39: 117–129

    Article  MATH  MathSciNet  Google Scholar 

  21. Nazareth, J. (1991). The homotopy principle and algorithms for linear programming. SIAM Journal on Optimization, 1: 316–332

    Article  MATH  MathSciNet  Google Scholar 

  22. Pardalos, P., Sandstrom, M. & Zopounidis, C. (1997). On the use of optimization models for portfolio selection: A review and some computational results. Computational Economics, 7: 227–244

    Article  MathSciNet  Google Scholar 

  23. Philippe, J. (2006). Value at Risk: The New Benchmark for Managing Financial Risk (3rd Edition). McGraw-Hill, New York

    Google Scholar 

  24. Raber, U. (1998). A simplicial branch-and-bound method for solving nonconvex all-quadratic programs. Journal of Global Optimization, 13: 417–432

    Article  MATH  MathSciNet  Google Scholar 

  25. Sahinidis, N. (1996). BARON: a general purpose optimizaton software package. Journal of Global Optimization, 8: 201–205

    Article  MATH  MathSciNet  Google Scholar 

  26. Saxena, A., Bonami, P. & Lee, J. (2011). Convex relaxations of nonconvex mixed integer quadratically constrained programs: projected formulations. Mathematical Programming, 130: 359–413

    Article  MATH  MathSciNet  Google Scholar 

  27. Sherali, H. & Adams, W. (1999). A Reformulated-Linerization Technique for Solving Discrete and Continuous Nonconvex Problems. Kluwer Academic Publishers, Dordrecht

    Book  Google Scholar 

  28. Sherali, H. & Tuncbilek, C. (1995). A reformulation-convexification approach for solving nonconvex quadratic programming problems. Journal of Global Optimization, 7: 1–31

    Article  MATH  MathSciNet  Google Scholar 

  29. Shor, N. (1987). Quadratic optimization problems. Soviet Journal of Computer and Systems Sciences, 25: 1–11

    MATH  MathSciNet  Google Scholar 

  30. Tian, Y., Fang, S.-C., Deng, Z. & Xing, W. (2013). Computable representation of the cone of nonnegative quadratic forms over a general second-order-cone and its application to completely positive programming. Journal of Industrial and Management Optimization, 9: 703–721

    Article  MATH  MathSciNet  Google Scholar 

  31. Yang, G., Huang, S. & Chen, W. (2007). An utilities based approach for multi-period dynamic portfolio selection. Journal of Systems Science and Systems Engineering, 16: 277–286

    Article  Google Scholar 

  32. Zhu, S., Li, D. & Sun, X. (2010). Portfolio selection with marginal risk control. The Journal of Computational Finance, 14: 3–28

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Management, University of Chinese Academy of Sciences, Beijing, 100049, China

    Zhibin Deng

  2. Industrial and Systems Engineering Department, North Carolina State University, Raleigh, NC, 27695, USA

    Zhibin Deng & Shu-Cherng Fang

  3. Department of Mathematics, Shanghai University, Shanghai, 200444, China

    Yanqin Bai

  4. School of Business Administration, Southwestern University of Finance and Economics, Chengdu, 611130, China

    Ye Tian

  5. Department of Mathematical Sciences, Tsinghua University, Beijing, 100084, China

    Wenxun Xing

Authors
  1. Zhibin Deng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yanqin Bai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shu-Cherng Fang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ye Tian
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Wenxun Xing
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ye Tian.

Additional information

This work was supported by the Edward P. Fitts Fellowship at North Carolina State University, the National Natural Science Foundation of China Grant Numbers 11171177, 11371216 and 11371242, and the US National Science Foundation Grant No. DMI-0553310.

Zhibin Deng received the BS and MS from Tsinghua University in 2007 and 2009 respectively, and the PhD from North Carolina State University in 2013. He was a research assistant in the US Army Research Office since 2011. He received Edwards P. Fitts Fellowship for his excellent academic record when admitted to North Carolina State University. He is the author or coauthor of papers published in European Journal of Operational Research, Journal of Operations Research Society of China and Journal of Industrial and Management Optimizati. His research interests include quadratic optimization, linear conic optimization and nonlinear optimization.

Yanqin Bai is a professor in the Department of Mathematics at Shanghai University. She received her Ph.D. from Shanghai University in 1996. She held a research fellow and postdoctoral research fellow position in Delft University of Technology in Netherlands during the period of 2001–2004. Her research interests are conic programming and interior-point methods.

Shu-Cherng Fang is the Walter Clark Chair and Alumni Distinguished Graduate Professor in the Department of Industrial & Systems Engineering and Gradute Program in Operations Research at NC State University. His key research interest is on optimization thery and algorithms with real life applications such as intelligent human-machine decision support systems, terrain data representation, logistics and supply chain management, telecommunications and bio-informatics. He received his Bachelor’s degree from the National Tsing Hua University in Taiwan and PhD degree from Northwestern University in US. Before he joined NC State University, Dr. Fang had been working at AT&T Engineering Research Center, AT&T Bell Laboratories, and AT&T Corporate Headquarters. He is also associated with many universities in Australia, China, Hong Kong and Taiwan. He has published a few journal articles and books. He is the Founding Editor-in-Chief of Fuzzy Optimization and Decision Making. His new book, coauthored by Prof. Wenxun Xing of Tsinghua University, on “Linear Conic Optimization” has just been published by the Science Press in August, 2013.

Tian Ye received the PhD degree in December 2012, from Industrial and Systems Engineering, North Carolina State University, USA. He is currently an assistant professor in the School of Business Administration, Southwestern University of Finance and Economics, Chengdu. He is the author or coauthor of papers published in major journals such as Journal of Industrial and Management Optimization, Algorithms, Journal of the Operations Research Society of China, among others. His research interests include quadratic programming problem, linear conic programming problem, algorithm designing, portfolio selection, project management, and major component detection and analysis.

Wenxun Xing is a professor in the Department of Mathematical Sciences, Tsinghua University, Beijing China. He received the BS degree in Mathematics from Peking University, China, in 1982 and received the PhD degree in Operations Research in 1997 in the Department of Applied Mathematics, Tsinghua University. His current research interests include conic programming, combinatorial optimization, global optimization etc. He has published over 50 papers and 6 books. He is now a senior member of the OR Society of China, a vice-director of the Mathematical Programming Branch of OR Society of China.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Deng, Z., Bai, Y., Fang, SC. et al. A branch-and-cut approach to portfolio selection with marginal risk control in a linear conic programming framework. J. Syst. Sci. Syst. Eng. 22, 385–400 (2013). https://doi.org/10.1007/s11518-013-5234-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11518-013-5234-5

Keywords

Search

Navigation