Security and Reliability Analysis of Relay Selection in Cognitive Relay Networks

Abstract

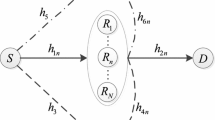
Improving security and reliability is a main concern in many wireless transmission systems. In this paper, we explore the security and reliability in cognitive relay networks with an eavesdropper and multiple relays where the decode-and-forward (DF) protocol is considered. We propose a novel cognitive relay selection to improve the security and reliability of the considered system. The most important contribution is that we obtain the cumulative distribution functions (CDFs) of the channels from the selected relay to the destination and to the eavesdropper, respectively, which makes other related theoretical research possible. Furthermore, based on the proposed relay selection criterion, we derive the accurate closed-form outage probability and intercept probability of the considered system. At last, simulation results verify the correctness of our derivations. Interestingly, although the relay selection is based on the relay-destination channel and the relay-eavesdropper channel, it can be seen from the theoretical results that the reliability performance is completely irrelevant to the relay-eavesdropper channel’s statistical characteristics, whereas the security performance is entirely independent of statistical characteristics of the relay-destination channel. In addition, the security performance is always improved with the increasing number of relays, but the reliability performance is not proportional to the number of relays any more when the number of relays reaches a certain value.

Appendices

Appendix 1

When $j \ge 1$, the result of $G\left( {z,j} \right)$ is derived as follows:

$$\begin{aligned} G\left( {z,j} \right)&= \int _z^{ + \infty } {\frac{1}{{{t^{j +1}}}}{e^{ - t}}dt} = \int _z^{ + \infty } {\frac{{{e^{ - t}}}}{{-j}}d{t^{ - j}}} = \frac{{{e^{ - z}}{z^{ - j}}}}{j} -\frac{1}{j}\int _z^{ + \infty } {{t^{ - j}}{e^{ - t}}dt} \nonumber \\&= \frac{{{e^{ - z}}{z^{ - j}}}}{j} + \frac{{{{\left( { - 1} \right) }^1}{e^{ - z}}{z^{ - j + 1}}}}{{j\left( {j - 1} \right) }} +\frac{1}{{j\left( {j - 1} \right) }}\int _z^{ + \infty } {{t^{ - j +1}}{e^{ - t}}dt} \nonumber \\&= \sum \limits _{k = 0}^{j - 1} {\frac{{{{\left( { - 1} \right) }^k}{e^{ - z}}{z^{k - j}}}}{{j\left( {j - 1} \right) \cdots \left( {j - k} \right) }}} + \frac{{{{\left( { - 1} \right) }^j}}}{{j!}}{{\mathrm{E}}_1}\left( z \right) . \end{aligned}$$

(37)

Appendix 2

Let ${\gamma _k} = {{{\gamma _{kD}}} /{{\gamma _{kE}}}}$, the PDF ${\gamma _{{k^{\mathrm{*}}}D}}$ can be obtained by

$$\begin{aligned} {f_{{\gamma _{{k^{*}}D}}}}\left( x \right) = \int _0^{ + \infty } {\frac{{{f_{{\gamma _{kD}},{\gamma _k}}} \left( {x,z} \right) }}{{{f_{{\gamma _k}}}\left( z \right) }} {f_{{\gamma _{{k^{*}}}}}}\left( z \right) } dz. \end{aligned}$$

(38)

The CDF of ${\gamma _k}$ can be expressed as

$$\begin{aligned} {F_{{\gamma _k}}}\left( z \right) = \int _0^\infty {\frac{1}{{{{\bar{\gamma } }_{RE}}}}{e^{ - \frac{y}{{{{\bar{\gamma } }_{RE}}}}}}\left( {1 - {e^{ - \frac{{zy}}{{{{\bar{\gamma } }_{RD}}}}}}} \right) } dy = 1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} +{{\bar{\gamma } }_{RE}}z}}. \end{aligned}$$

(39)

By taking the derivative of (39), we have

$$\begin{aligned} {f_{{\gamma _k}}}\left( z \right) = \frac{{{{\bar{\gamma } }_{RD}} {{\bar{\gamma } }_{RE}}}}{{{{\left( {{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z} \right) }^2}}}. \end{aligned}$$

(40)

According to (7), we can also get the CDF of ${\gamma _{{k^*}}} =\mathop {\max }\limits _{k \in {\mathbf{D}}} \left\{ {{{{\gamma _{kD}}} / {{\gamma _{kE}}}}} \right\}$ as

$$\begin{aligned} {F_{{\gamma _{{k^*}}}}}\left( z \right)&=\Pr \left\{ {\mathop {\max }\limits _{k \in {\mathbf{D}}, \left| {\mathbf{D}} \right| = K} \left\{ {\frac{{{\gamma _{kD}}}}{{{\gamma _{kE}}}}} \right\}< z} \right\} \nonumber \\&= \prod \limits _{k \in {\mathbf{D}},\left| {\mathbf{D}} \right| = K} {\Pr \left\{ {\frac{{{\gamma _{kD}}}}{{{\gamma _{kE}}}} < z} \right\} } = {\left( {1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) ^K}. \end{aligned}$$

(41)

Taking the derivative of (41), we obtain the corresponding PDF of ${\gamma _{{k^*}}}$ as follows:

$$\begin{aligned} {f_{{\gamma _{{k^*}}}}}\left( z \right) = K{\left( {1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) ^{K - 1}} \frac{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}{{{{\left( {{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z} \right) }^2}}}. \end{aligned}$$

(42)

Thus, the joint CDF ${F_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right)$ is derived as

$$\begin{aligned} {F_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right)&= \Pr \left\{ {{\gamma _{kD}}< x,{\gamma _k}< z} \right\} \nonumber \\&= \Pr \left\{ {{\gamma _{kD}}< x,{\gamma _{kE}} > \frac{x}{z}} \right\} + \Pr \left\{ {{\gamma _{kE}}< \frac{x}{z},{\gamma _{kD}} < z{\gamma _{kE}}} \right\} \nonumber \\&= \int _{\frac{x}{z}}^\infty {\frac{1}{{{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{y}{{{{\bar{\gamma } }_{RE}}}}}} \left( {1 - {e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}}}}}} \right) } dy + \int _0^{\frac{x}{z}} {\frac{1}{{{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{y}{{{{\bar{\gamma } }_{RE}}}}}}\left( {1 - {e^{ - \frac{{zy}}{{{{\bar{\gamma } }_{RD}}}}}}} \right) } dy\nonumber \\&= \frac{{z{{\bar{\gamma } }_{RE}}}}{{{{\bar{\gamma } }_{RD}} + z{{\bar{\gamma } }_{RE}}}} \left( {1 - {e^{ - \frac{{{{\bar{\gamma } }_{RD}} + z{{\bar{\gamma } }_{RE}}}}{{{{\bar{\gamma } }_{RD}} {{\bar{\gamma } }_{RE}}}}\frac{x}{z}}}} \right) . \end{aligned}$$

(43)

Therefore, after taking the derivative of (43), we get the joint PDF ${f_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right)$ as follows:

$$\begin{aligned} {f_{{\gamma _{kD}},{\gamma _k}}}\left( {x,z} \right) =\frac{{{\partial ^2}{F_{{\gamma _{kD}},{\gamma _k}}} \left( {x,z} \right) }}{{\partial x\partial z}} =\frac{x}{{{z^2}{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{x}{{z{{\bar{\gamma } }_{RE}}}}}}{e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}}}}}. \end{aligned}$$

(44)

By substituting (40), (42) and (44) into (38), we get

$$\begin{aligned} {f_{{\gamma _{{k^*}D}}}}\left( x \right)&= \int _0^{ + \infty } {\frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}{z^2}}} {e^{ - \frac{{{{\bar{\gamma } }_{RD}} + z{{\bar{\gamma } }_{RE}}}}{{{{\bar{\gamma } }_{RE}}{{\bar{\gamma } }_{RD}}z}}x}}K{{\left( {1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) }^{K - 1}}} dz\nonumber \\&= K{e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}}}}}\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m}\int _0^{ + \infty } {{{\left( {\frac{{{{\bar{\gamma } }_{RD}}t}}{{{{\bar{\gamma } }_{RD}}t + {{\bar{\gamma } }_{RE}}}}} \right) }^m}\frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}{e^{ - \frac{x}{{{{\bar{\gamma } }_{RE}}}}t}}} dt} \nonumber \\&= K\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m}\int _{{{\bar{\gamma } }_{RE}}}^{ + \infty } {{{\left( {1 - \frac{{{{\bar{\gamma } }_{RE}}}}{z}} \right) }^m}\frac{x}{{\bar{\gamma }_{RD}^2{{\bar{\gamma } }_{RE}}}}{e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}z}}} dz} \nonumber \\&= K\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m}\int _{{{\bar{\gamma } }_{RE}}}^{ + \infty } {\sum \limits _{j = 0}^m {\left( {\begin{array}{c} m\\ j \end{array}} \right) {{\left( { - {{\bar{\gamma } }_{RE}}} \right) }^j}} \frac{x}{{\bar{\gamma }_{RD}^2{{\bar{\gamma } }_{RE}}{z^j}}}{e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}z}}} dz}. \end{aligned}$$

(45)

The final closed-form result of ${f_{{\gamma _{{k^{*}}D}}}} \left( x\right)$ is not used in the subsequent derivation process, so we needn’t give the final closed-form expression of ${f_{{\gamma _{{k^{*}}D}}}}\left( x\right)$.

Substituting (40), (42) and (44) into (38), meanwhile, we integrate the PDF of $\gamma _{{k^{*}}D}$, then the final result of the CDF of $\gamma _{{k^{*}}D}$ is derived as (46).

$$\begin{aligned} {F_{{\gamma _{{k^{*}}D}}}}\left( x \right)&= \int _0^x {\int _0^{ + \infty } {\frac{t}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}{z^2}}}{e^{ - \frac{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}{{{{\bar{\gamma } }_{RE}}{{\bar{\gamma } }_{RD}}z}}t}}K{{\left( {1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) }^{K - 1}}} } dzdt\nonumber \\&= Kx\int _0^{ + \infty } {\left[ {\frac{{{{\bar{\gamma } }_{RD}}}}{{{{\left( {{{\bar{\gamma } }_{RD}}t + x} \right) }^2}}}\left( {1 - {e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}}}}}{e^{ - t}}} \right) - \frac{1}{{{{\bar{\gamma } }_{RD}}t +x}}{e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}}}}}{e^{ - t}}} \right] {{\left( {\frac{x}{{{{\bar{\gamma } }_{RD}}t + x}}} \right) }^{K - 1}}dt} \nonumber \\&= K{x^K}\int _x^{ + \infty } {\frac{1}{{{z^{K + 1}}}}dz} - K{\left( {\frac{x}{{{{\bar{\gamma } }_{RD}}}}} \right) ^K}\int _{\frac{x}{{{{\bar{\gamma } }_{RD}}}}}^{ + \infty } {\left( {\frac{1}{{{t^{K + 1}}}}{e^{ - t}} + \frac{1}{{{t^K}}}{e^{ - t}}} \right) dt} \nonumber \\&= 1 - K{\left( {\frac{x}{{{{\bar{\gamma } }_{RD}}}}} \right) ^K} \left[ {G\left( {\frac{x}{{{{\bar{\gamma } }_{RD}}}},K} \right) + G\left( {\frac{x}{{{{\bar{\gamma } }_{RD}}}},K - 1} \right) }\right] . \end{aligned}$$

(46)

Appendix 3

The joint CDF ${F_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right)$ is derived as

$$\begin{aligned} {F_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right)&= \Pr \left\{ {{\gamma _{kE}}< x,{\gamma _k} < z} \right\} \nonumber \\&= \frac{{z{{\bar{\gamma } }_{RE}}}}{{{{\bar{\gamma } }_{RD}} +z{{\bar{\gamma }}_{RE}}}} - {e^{ - \frac{y}{{{{\bar{\gamma } }_{RE}}}}}} + \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} +z{{\bar{\gamma }}_{RE}}}}{e^{ - \frac{{{{\bar{\gamma } }_{RD}} + z{{\bar{\gamma }}_{RE}}}}{{{{\bar{\gamma } }_{RD}} {{\bar{\gamma }}_{RE}}}}x}} \end{aligned}$$

(47)

Therefore, after taking the derivative of (47), we get the joint PDF ${f_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right)$ as

$$\begin{aligned} {f_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right) =\frac{{{\partial ^2}{F_{{\gamma _{kE}},{\gamma _k}}} \left( {x,z} \right) }}{{\partial x\partial z}} =\frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{x}{{{{\bar{\gamma } }_{RE}}}}}} {e^{ - \frac{{zx}}{{{{\bar{\gamma } }_{RD}}}}}}. \end{aligned}$$

(48)

Therefore, the expression of ${f_{{\gamma _{{k^{*}}E}}}}(x)$ is derived as

$$\begin{aligned} {f_{{\gamma _{{k^{*}}E}}}}\left( x \right)&= \int _0^{ + \infty } {\frac{{{f_{{\gamma _{kE}},{\gamma _k}}}\left( {x,z} \right) }}{{{f_{{\gamma _k}}}\left( z \right) }} {f_{{\gamma _{{k^{*}}}}}}\left( z \right) } dz\nonumber \\&= \frac{{Kx}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{x}{{{{\bar{\gamma } }_{RE}}}}}}\int _0^{ + \infty } {{e^{ -\frac{{zx}}{{{{\bar{\gamma } }_{RD}}}}}}\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) }^m}} } dz\nonumber \\&= \frac{K}{{{{\bar{\gamma } }_{RE}}}}\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{x}{{{{\bar{\gamma } }_{RE}}}}} \right) }^m}\int _{\frac{x}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{{{e^{ - t}}}}{{{t^m}}}} } dt. \end{aligned}$$

(49)

The CDF of ${\gamma _{{k^{*}}E}}$ can be derived as (50).

$$\begin{aligned} {F_{{\gamma _{{k^{*}}E}}}}\left( x \right)&= \int _0^x {\int _0^{ + \infty } {\frac{{Kt}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}{e^{ - \frac{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}t}}{{\left( {1 - \frac{{{{\bar{\gamma } }_{RD}}}}{{{{\bar{\gamma } }_{RD}} + {{\bar{\gamma } }_{RE}}z}}} \right) }^{K - 1}}} } dzdt\nonumber \\&= K\sum \limits _{k = 0}^{K - 1} \left( {\begin{array}{c} {K - 1}\\ k \end{array}} \right) {{\left( { - \frac{x}{{{{\bar{\gamma } }_{RE}}}}} \right) }^{k + 1}}\nonumber \\&\quad \left( {\frac{{ - 1}}{{k + 1}} {{\left( {\frac{{{{\bar{\gamma } }_{RE}}}}{x}} \right) }^{k + 1}} +\int _{\frac{x}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{{{e^{- z}}}}{{{z^{k + 2}}}}dz} + \int _{\frac{x}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{{{e^{ - z}}}}{{{z^{k + 1}}}}dz}}\right) \nonumber \\&= 1 + K\sum \limits _{k = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ k \end{array}} \right) {{\left( { - \frac{x}{{{{\bar{\gamma } }_{RE}}}}} \right) }^{k + 1}}\left[ {G\left( {\frac{x}{{{{\bar{\gamma } }_{RE}}}},k + 1} \right) + G\left( {\frac{x}{{{{\bar{\gamma } }_{RE}}}},k} \right) } \right] }. \end{aligned}$$

(50)

Appendix 4

$$\begin{aligned} H\left( {z,a,j} \right)&= \int _z^{ + \infty } {\frac{1}{{\left( {1 + at} \right) {t^{j + 1}}}}{e^{ - t}}} dt\nonumber \\&= \sum \limits _{i = 0}^j {{{\left( { - a} \right) }^i} \int _z^{ + \infty } {\frac{1}{{{t^{j + 1 - i}}}}{e^{ - t}}} dt} + {\left( { - a} \right) ^{j + 1}}\int _z^{ + \infty } {\frac{1}{{1 + at}}{e^{ - t}}} dt\nonumber \\&= \sum \limits _{i = 0}^{j - 1} {{{\left( { - a} \right) }^i}G \left( {z,j - i} \right) } + {\left( { - a} \right) ^j} \left[ {{{\mathrm{E}}_1}\left( z \right) - {e^{\frac{1}{a}}}{{\mathrm{E}}_1} \left( {\frac{{1 + az}}{a}} \right) } \right] . \end{aligned}$$

(51)

Appendix 5

By using of (45), the term $\Pr \left\{ {\frac{{{\gamma _{{k^*}D}}}}{{{\gamma _{PD}} + 1}} < T} \right\}$ can be derived as follows:

$$\begin{aligned} \Pr \left\{ {\frac{{{\gamma _{{k^*}D}}}}{{{\gamma _{PD}} + 1}} < T}\right\}&= \int _0^{ + \infty } {{f_{{\gamma _{{k^{*}}D}}}} \left( x \right) \Pr \left\{ {{\gamma _{PD}} > \frac{x}{T} - 1} \right\} } dx\nonumber \\&=\int _T^{ + \infty } {{f_{{\gamma _{{k^{*}}D}}}} \left( x \right) {e^{ - \frac{1}{{{{\bar{\gamma } }_{PD}}}} \left( {\frac{x}{T} - 1} \right) }}} dx + {F_{{\gamma _{{k^{*}}D}}}} \left( T \right) , \end{aligned}$$

(52)

where

$$\begin{aligned}&\int _T^{ + \infty } {{f_{{\gamma _{{k^{*}}D}}}}\left( x \right) {e^{- \frac{1}{{{{\bar{\gamma } }_{PD}}}}\left( {\frac{x}{T} - 1} \right) }}} dx\nonumber \\&\quad = \int _T^{ + \infty } {K\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m} \int _{{{\bar{\gamma } }_{RE}}}^{ + \infty } {\sum \limits _{j = 0}^m}}} \nonumber \\&\qquad \left( {\begin{array}{c} m\\ j \end{array}} \right) {\left( { - {{\bar{\gamma } }_{RE}}} \right) ^j}\frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}\frac{1}{{{z^j}}} {e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}z}}dz {e^{ - \frac{1}{{{{\bar{\gamma } }_{PD}}}} \left( {\frac{x}{T} - 1} \right) }}dx\nonumber \\&\quad = \frac{{KT}}{{{{\bar{\gamma } }_{RD}}}} \sum \limits _{m = 0}^{K - 1}\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m} \int _{{{\bar{\gamma } }_{RE}}}^{ + \infty } \sum \limits _{j = 0}^m\nonumber \\&\qquad \left[ \left( {\begin{array}{c} m\\ j \end{array}} \right) {\left( - {{\bar{\gamma } }_{RE}}\right) }^j \frac{1}{{{z^j}}}\frac{{{{\bar{\gamma }}_{PD}}T}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}} +{{\bar{\gamma } }_{PD}}Tz}}\left( {1 + \frac{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}{{\bar{\gamma }}_{PD}}}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}} +{{\bar{\gamma } }_{PD}}Tz}}} \right) {e^{ -\frac{{Tz}}{{{{\bar{\gamma } }_{RD}} {{\bar{\gamma } }_{RE}}}}}}\right] dz\nonumber \\&\quad = \frac{{KT}}{{{{\bar{\gamma } }_{RD}}}} \sum \limits _{m = 1}^{K - 1}\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m} \sum \limits _{j = 1}^m{\left( {\begin{array}{c} m\\ j \end{array}} \right) {{\left( { - \frac{T}{{{{\bar{\gamma } }_{RD}}}}} \right) }^j}}\nonumber \\&\qquad \left[ \int _{\frac{T}{{{{\bar{\gamma } }_{RD}}}}}^{ + \infty } {\frac{{{{\bar{\gamma } }_{PD}}}}{{\left( {1 + {{\bar{\gamma } }_{PD}}t} \right) {t^j}}}{e^{ - t}}dt} - \int _{\frac{T}{{{{\bar{\gamma } }_{RD}}}}}^{ + \infty } {\frac{1}{{{t^j}}}{e^{ - t}}d\frac{{{{\bar{\gamma } }_{PD}}}}{{1 + {{\bar{\gamma } }_{PD}}t}}} \right] \nonumber \\&\quad = \frac{{K{{\bar{\gamma } }_{PD}}T}}{{{{\bar{\gamma } }_{RD}} +{{\bar{\gamma } }_{PD}}T}}{e^{ - \frac{T}{{{{\bar{\gamma } }_{RD}}}}}} - \frac{{K{{\bar{\gamma } }_{PD}}T}}{{{{\bar{\gamma } }_{RD}}}}\nonumber \\&\qquad \times \sum \limits _{m = 1}^{K - 1} \left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m} \sum \limits _{j = 1}^m{\left( {\begin{array}{c} m\\ j \end{array}} \right) {\left( -\frac{T}{{{{\bar{\gamma } }_{RD}}}}\right) ^j}} \int _{\frac{T}{{{{\bar{\gamma } }_{RD}}}}}^{ + \infty } \frac{j}{{\left( {1 + {{\bar{\gamma } }_{PD}}t} \right) {t^{j + 1}}}}{e^{ - t}}dt \nonumber \\&\quad = \frac{{K{{\bar{\gamma } }_{PD}}T}}{{{{\bar{\gamma } }_{RD}} +{{\bar{\gamma } }_{PD}}T}}{e^{ - \frac{T}{{{{\bar{\gamma } }_{RD}}}}}} - \frac{{K{{\bar{\gamma } }_{PD}}T}}{{{{\bar{\gamma } }_{RD}}}} \nonumber \\&\qquad \times \sum \limits _{m = 1}^{K - 1}\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - 1} \right) }^m} \sum \limits _{j = 1}^m \left( {\begin{array}{c} m\\ j \end{array}} \right) {\left( -\frac{T}{{{{\bar{\gamma } }_{RD}}}} \right) }^{j} jH\left( {\frac{T}{{{{\bar{\gamma }}_{RD}}}}, {{\bar{\gamma } }_{PD}},j} \right) . \end{aligned}$$

(53)

Appendix 6

By using of (49), the term $\Pr \left\{ {\frac{{{\gamma _{{k^*}E}}}}{{{\gamma _{PE}} + 1}} > T} \right\}$ can be derived as follows:

$$\begin{aligned}&\Pr \left\{ {\frac{{\gamma _{{k^*}E}^{{\alpha _R}}}}{{{\gamma _{PE}} + 1}} > T} \right\} = \int _0^{ + \infty } {{f_{{\gamma _{{k^{*}}E}}}}\left( x \right) \Pr \left\{ {{\gamma _{PE}} < \frac{x}{T} - 1} \right\} } dx\nonumber \\&\quad = {\mathrm{1}} - {F_{{\gamma _{{k^{*}}E}}}}\left( T \right) \nonumber \\&\qquad -\int _T^{ + \infty } {\frac{{Kx}}{{{{\bar{\gamma }}_{RD}} {{\bar{\gamma } }_{RE}}}}\int _{{{\bar{\gamma } }_{RD}}}^{ + \infty } {\sum \limits _{m = 0}^{K - 1}{\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{{{{\bar{\gamma } }_{RD}}}}{t}} \right) }^m}\frac{1}{{{{\bar{\gamma } }_{RE}}}} {e^{ - \frac{x}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}t}}}} dt{e^{ - \frac{1}{{{{\bar{\gamma } }_{PE}}}}\left( {\frac{x}{T} - 1} \right) }}} dx\nonumber \\&\quad = {\mathrm{1}} - {F_{{\gamma _{{k^{*}}E}}}}\left( T \right) -\frac{{KT}}{{{{\bar{\gamma } }_{RE}}}} \nonumber \\&\qquad \times \int _{{{\bar{\gamma } }_{RD}}}^{ + \infty } {\sum \limits _{m = 0}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{{{{\bar{\gamma } }_{RD}}}}{t}} \right) }^m}\frac{{{{\bar{\gamma } }_{PE}}T}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}} + {{\bar{\gamma } }_{PE}}Tt}} \left( {1 + \frac{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}} {{\bar{\gamma } }_{PE}}}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}} + {{\bar{\gamma } }_{PE}}Tt}}} \right) {e^{ - \frac{{Tt}}{{{{\bar{\gamma } }_{RD}}{{\bar{\gamma } }_{RE}}}}}}}} dt\nonumber \\&\quad = {\mathrm{1}} - {F_{{\gamma _{{k^{*}}E}}}}\left( T \right) - \frac{{KT}}{{{{\bar{\gamma } }_{RE}}}} \left( {\int _{\frac{T}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{{{{\bar{\gamma } }_{PE}}}}{{1 + {{\bar{\gamma } }_{PE}}z}} {e^{- z}}dz} - \int _{\frac{T}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {{e^{ - z}}d\frac{{{{\bar{\gamma } }_{PE}}}}{{1 + {{\bar{\gamma }}_{PE}}z}}} } \right) \nonumber \\&\qquad -\frac{{KT}}{{{{\bar{\gamma } }_{RE}}}} \sum \limits _{m = 1}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{T}{{{{\bar{\gamma } }_{RE}}}}} \right) }^m}\left[ {\int _{\frac{T}{{{{\bar{\gamma } }_{RE}}}}}^{ +\infty } {\frac{{{{\bar{\gamma } }_{PE}}}}{{\left( {1 + {{\bar{\gamma } }_{PE}}z} \right) {z^m}}}{e^{ - z}}dz} -\int _{\frac{T}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{1}{{{z^m}}}{e^{ - z}}d\frac{{{{\bar{\gamma } }_{PE}}}}{{1 + {{\bar{\gamma } }_{PE}}z}}} } \right] } \nonumber \\&\quad = {\mathrm{1}} - {F_{{\gamma _{{k^{*}}E}}}}\left( T \right) +\frac{{KT}}{{{{\bar{\gamma } }_{RE}}}}\sum \limits _{m = 1}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{T}{{{{\bar{\gamma } }_{RE}}}}} \right) }^m}\int _{\frac{T}{{{{\bar{\gamma } }_{RE}}}}}^{ + \infty } {\frac{{m{{\bar{\gamma } }_{PE}}}}{{\left( {1 + {{\bar{\gamma }}_{PE}}z} \right) {z^{m + 1}}}} {e^{ - z}}dz} } \nonumber \\&\quad = {\mathrm{1}} - {F_{{\gamma _{{k^{*}}E}}}}\left( T \right) + \frac{{K{{\bar{\gamma } }_{PE}}T}}{{{{\bar{\gamma }}_{RE}}}} \sum \limits _{m = 1}^{K - 1} {\left( {\begin{array}{c} {K - 1}\\ m \end{array}} \right) {{\left( { - \frac{T}{{{{\bar{\gamma } }_{RE}}}}} \right) }^m}mH\left( {\frac{T}{{{{\bar{\gamma }}_{RE}}}}, {{\bar{\gamma } }_{PE}},m} \right) }. \end{aligned}$$

(54)