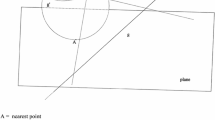
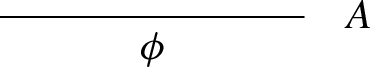Skip to main content
SpringerLink
Log in

A meaning explanation for HoTT

  • S.I.: Foundations of Mathematics
  • Published:
Synthese Aims and scope Submit manuscript

Abstract

In the Univalent Foundations of mathematics spatial notions like “point” and “path” are primitive, rather than derived, and all of mathematics is encoded in terms of them. A Homotopy Type Theory is any formal system which realizes this idea. In this paper I will focus on the question of whether a Homotopy Type Theory (as a formalism for the Univalent Foundations) can be justified intuitively as a theory of shapes in the same way that ZFC (as a formalism for set-theoretic foundations) can be justified intuitively as a theory of collections. I first clarify what such an “intuitive justification” should be by distinguishing between formal and pre-formal “meaning explanations” in the vein of Martin-Löf. I then go on to develop a pre-formal meaning explanation for HoTT in terms of primitive spatial notions like “shape”, “path” etc.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. For standard introductions to UF and HoTT, see Univalent Foundations Program (2013), Pelayo and Warren (2014), Shulman (2016), Voevodsky (2014), and Grayson (2017). For the ideas that led to the homotopy interpretation of type theory see Awodey and Warren (2009), and Warren (2008). For some of the earlier writing that led to the ideas for UF see Voevodsky (2010), Voevodsky (2010), and Voevodsky (2006). For a discussion of the sense in which UF is a foundation of mathematics and connections to mathematical structuralism, see Tsementzis (2016), Tsementzis (2017), Tsementzis and Halvorson (2017), and Awodey (2014). For some philosophical issues associated to HoTT see Ladyman and Presnell (2015), Corfield (2016), Corfield (2015), and Rodin (2014).

  2. For an account of ZFC’s emergence as a standard of rigour see Burgess (2014).

  3. Some facts are already known about the technical relationship between ZFC and HoTT. For example, the simplicial model of univalence (Kapulkin et al. 2014) gives an interpretation of HoTT into ZFC supplemented with two inaccessible cardinals and Cubical Type Theory (CTT) (Bezem et al. 2014; Cohen et al. 2015) is expected to be interpretable into a constructive theory like CZF (Aczel 1978). In the other direction, the 0-types (“h-sets”) in a univalent universe are known to model (variants of) Lawvere’s ETCS (cf. Lawvere 2005) known to be equiconsistent with the system BZC.

  4. There are other, less specific, ways of understanding autonomy. The autonomy that I speak of is perhaps closest to the “justificatory autonomy” of foundations as made precise by Linnebo and Pettigrew (2011).

  5. For example, the formal system ZFC can be defined with S the set of well-formed first-order formulas over the signature with \(\in \) the only non-logical symbol and with R the usual rules for classical first-order logic together with rules of the form

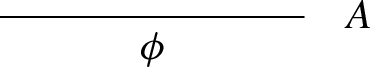
    figure c

    for every axiom \(\phi \) of ZFC. A meaning explanation for ZFC would then need to give a meaning to the symbol \(\in \) such that the axiom-rules such as A are justified, which in this case means simply that \(\phi \) can be argued to be true (from no premises). For example, for \(\phi \) the axiom for the empty set we would have to argue that it is true under the particular meaning of \(\in \) that there is an entity with no elements.

  6. This name was suggested by an anonymous referee.

  7. This does not mean that any formalization for UF will be based on MLTT. UF is no more tied to MLTT than set-theoretic foundations are tied to Russell’s Type Theory. I take up this point in the conclusion.

  8. For more details see Martin-Löf (1982, 1996) as well as remarks in the original Martin-Löf (1984). A good exposition can be found in Dybjer (2012).

  9. More precisely, that a has a canonical program of the canonical type A as a value.

  10. The justification for UIP goes roughly as follows: insofar as we have a proof of identity, we no longer care to distinguish between the two terms shown to be identical; therefore all that matters is that they are identical, which means that there should be only one canonical term demonstrating this fact. See Dybjer (2012, p. 8) for further discussion on this point and Hou (2017, p. 18) for more on the incompatibility of UIP with univalence.

  11. Furthermore, let me note that this also means that MLTT and HoTT should be viewed as fundamentally distinct formal systems and not species of the same genus (a genus one may broadly label “dependent type theories”). Although sociologically inevitable, to call HoTT a type theory is, I think, conceptually a mistake. Any formalization of UF should rather be called a “shape theory” in much the same way that ZFC (or CZF, or ZF etc.) is called a “set theory”. Dependent Type Theories should strictly speaking be understood as those formal systems which can be given a Martin-Löf-style meaning explanation.

  12. The notation \(\omega \) here is used to emphasize that the universes are ordered, and there could be countably infinite of them, as well as in order to distinguish the indexing of the universes from the notation \(\mathbb {N}\). The use of set-theoretic language here is purely conventional, occurs at the meta-theory level, and carries no commitments.

  13. UniMath (Voevodsky et al. 2017) is the closest formal realization of my HoTT, at least insofar as one ignores the fact that it is built on top of Coq, which is itself based on the much stronger Calculus of Inductive Constructions. Alternatively, HoTT can be taken as the system described in the Appendix of Kapulkin et al. (2014) if we replace the rules of W-types with the rules for \(\mathbb {N}\) (which follow anyway as a special case of W-types). Clearly this is not the only system that adequately formalizes UF, nor is it clearly the most suitable one to receive a meaning explanation.

  14. There is an unfortunate terminological clash with Observational Type Theory (OTT), a variant of MLTT considered in Altenkirch and McBride (2006). The terminological connection between my use of “observation” here and the use of the same word in OTT is a coincidence.

  15. This is how “type dependency” is parsed in our meaning explanation.

  16. This slogan reflects the formal fact that in the formal models of the kind of type theories on which HoTT is based (e.g. models in terms of contextual categories) the rule for type constructors describe structure on these formal models (e.g. \(\varSigma \)-type structure on a contextual category), rather than properties. My decision to adopt the neologism here described is just a pre-formal reflection of this fact.

  17. This notion is technically referred to as homotopy equivalence, and if the reader has any intuition about this notion, then let us make clear that this is exactly the notion to which we are referring.

  18. Indeed, given the rules for transport above, we can derive the usual J-rule for identity types from the J which witnesses the fact that the identity map is an equivalence.

  19. It must be noted, however, that our presentation relies on the availability of \(\mathsf {Total}\) and \(\mathsf {Map}\) constructors, and the equivalence between the two sets of rules holds only modulo their availability.

  20. Essentially, the task of making this precise amounts to giving an interpretation of PA/HA into a theory with pure geometric content. In the setting of first-order logic, this is not entirely without precedent. See for example the work of Hellman and Shapiro (2013). More recently, in private communication, Harvey Friedman has suggested a way of interpreting \(Z_2\) (roughly, second-order arithmetic) into a first-order theory built out of purely geometric notions. Such efforts, especially the ones of Friedman that were motivated by similar considerations as the ones that motivate me here, could certainly help in fleshing out a purely geometric understanding of PA/HA, one that could then be used to give a more purely spatial justification to rules such as \(\mathbb {N}\)-Intro-2.

  21. A similar argument, discussing the intuitive content of homotopy types, has been put forward by Marquis (2013).

  22. If one is interested in pursuing such a line, then the groundbreaking way in which the material is presented in Hou (2017) will certainly prove an invaluable resource.

  23. This idea is developed further in Tsementzis and Halvorson (2017) based on the formal system in Tsementzis (2016).

  24. This has recently been argued in Corfield (2015).

References

  • Aczel, P. (1978). The type theoretic interpretation of constructive set theory. In L. P. A. MacIntrye & J. Paris (Eds.), Logic colloquium ’77 (Proc. Conf., Wroclaw, 1977), Stud. Logic Foundations Math. (vol. 96, pp. 55–66). Amsterdam, New York: North-Holland.

  • Altenkirch, T., & McBride, C. (2006). Towards observational type theory. Manuscript, available online.

  • Angiuli, C., Harper, R., & Wilson, T. (2016). Computational higher type theory I: Abstract cubical realizability. arXiv preprint arXiv:1604.08873

  • Awodey, S. (2014). Structuralism, Invariance and univalence. Philosophia Mathematica, 22(1), 1–11.

    Article  Google Scholar 

  • Awodey, S., & Warren, M. A. (2009). Homotopy theoretic models of identity types. In Mathematical proceedings of the Cambridge Philosophical Society, vol. 146, no 45, pp. 45–55.

  • Bezem, M., Coquand, T., & Huber, S. (2014). A model of type theory in cubical sets. In 19th International conference on types for proofs and programs (TYPES 2013), vol. 26, pp. 107–128.

  • Boolos, G. (1971). The iterative conception of set. The Journal of Philosophy, 68(8), 215–231.

    Article  Google Scholar 

  • Burgess, J. (2014). Rigor and structure. Oxford: Oxford University Press.

    Google Scholar 

  • Cartmell, J. (1986). Generalized algebraic theories and contextual categories. Annals of Pure and Applied Logic, 32, 209–243.

    Article  Google Scholar 

  • Cohen, C., Coquand, T., Huber, S., & Mörtberg, A. (2015). Cubical type theory: A constructive interpretation of the univalence axiom. https://www.math.ias.edu/~amortberg/papers/cubicaltt.pdf

  • Corfield, D. (2015). Reviving the philosophy of geometry. http://philsci-archive.pitt.edu/11809/

  • Corfield, D. (2016). Expressing “the structure of” in homotopy type theory. http://philsci-archive.pitt.edu/11862/

  • Dybjer, P. (2012). Program testing and the meaning explanations of intuitionistic type theory. Available at http://www.cse.chalmers.se/~peterd/papers/MartinLofFestschrift.pdf

  • Gelfand, M. (2009). We do not choose mathematics as our profession, it chooses us: Interview with Yuri Manin. Notices of the AMS, 56(10).

  • Grayson, D. (2017). An introduction to the univalent foundations for mathematicians. arXiv preprint. Available at https://arxiv.org/pdf/1711.01994.pdf

  • Hellman, G., & Shapiro, S. (2013). The classical continuum without points. Review of Symbolic Logic, 6(3), 488–512.

    Article  Google Scholar 

  • Hou, K. B. (2017). Higher-dimensional types in the mechanization of homotopy theory. Ph.D. thesis, CMU.

  • Kapulkin, K., Lumsdaine, P., & Voevodsky, V. (2014). The simplicial model of univalent foundations. arXiv:1211.2851v2

  • Ladyman, J., & Presnell, S. (2015). Identity in homotopy type theory, Part I: The justification of path induction. Philosophia Mathematica.

  • Lawvere, W. (2005). An elementary theory of the category of sets. Reprints in Theory and Applications of Categories, 12, 1–35.

    Google Scholar 

  • Linnebo, Ø., & Pettigrew, R. (2011). Category theory as an autonomous foundation. Philosophia Mathematica, pp. 1–30.

  • Marquis, J. P. (2013). Mathematical forms and forms of mathematics: leaving the shores of extensional mathematics. Synthese, 190(12), 2141–2164.

    Article  Google Scholar 

  • Martin-Löf, P. (1982). Constructive mathematics and computer programming. Studies in Logic and the Foundations of Mathematics, 104, 153–175.

    Article  Google Scholar 

  • Martin-Löf, P. (1984). Intuitionistic type theory. Bibliopolis.

  • Martin-Löf, P. (1987). Truth of a proposition, evidence of a judgement, validity of a proof. Synthese, 73, 407–420.

    Article  Google Scholar 

  • Martin-Löf, P. (1996). On the meanings of the logical constants and the justifications of the logical laws. Nordic Journal of Philosophical Logic, 1(1), 11–60.

    Google Scholar 

  • Pelayo, Á., & Warren, M. (2014). Homotopy type theory and Voevodsky’s univalent foundations. Bulletin of the American Mathematical Society, 51(4), 597–648.

    Article  Google Scholar 

  • Rodin, A. (2014). On constructive axiomatic method. Available at http://philsci-archive.pitt.edu/10986/

  • Shulman, M. (2016). Homotopy type theory: A synthetic approach to higher equalities. In E. Landry (Ed.) Categories for the working philosopher.

  • Tsementzis, D. (2016). First-order logic with isomorphism. arXiv preprint arXiv:1603.03092

  • Tsementzis, D. (2016). Univalent foundations as structuralist foundations. Synthese, pp. 1–35. https://doi.org/10.1007/s11229-016-1109-x.

    Article  Google Scholar 

  • Tsementzis, D. (2017). What is a higher-level set? Philosophia Mathematica. https://doi.org/10.1093/philmat/nkw032

  • Tsementzis, D., & Halvorson, H. (2017). Foundations and philosophy. Philosopher’s Imprint. http://philsci-archive.pitt.edu/13504/. Forthcoming

  • Univalent foundations program: Homotopy type theory: Univalent foundations of mathematics (2013). http://homotopytypetheory.org/book

  • Voevodsky, V. (2006). Foundations of mathematics and homotopy theory. https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/VV%20Slides.pdf

  • Voevodsky, V. (2010). The equivalence axiom and univalent models of type theory. Talk at CMU.

  • Voevodsky, V. (2010). Univalent foundations project. http://www.math.ias.edu/vladimir/files/univalent_foundations_project.pdf

  • Voevodsky, V. (2014). Subsystems and regular quotients of C-systems. arXiv:1406.5389, submitted pp. 1–11. arXiv:1406.7413

  • Voevodsky, V. (2014). Univalent foundations (lecture at the IAS). https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/2014_IAS.pdf

  • Voevodsky, V., Ahrens, B., & Grayson, D., et al. (2017). UniMath: Univalent mathematics. Available at https://github.com/UniMath

  • Warren, M. A. (2008). Homotopy theoretic aspects of constructive type theory. Ph.D. thesis, Carnegie Mellon University.

Download references

Acknowledgements

I would like to thank John Burgess, Harvey Friedman, Hans Halvorson, Bob Harper, and Colin McLarty for many helpful comments on several earlier drafts. I would also like to single out in thanks Harry Crane, both for his many insightful comments and questions on the many earlier versions of this paper, as well as for his encouragement and support. Finally, I would like to thank two anonymous referees for highly engaged and illuminating remarks that led to many substantial improvements to the paper. This work was partially supported by NSF CAREER-DMS-1554092 (P.I. Harry Crane).

Author information

Authors and Affiliations

  1. Brooklyn, NY, 11201, USA

    Dimitris Tsementzis

Authors
  1. Dimitris Tsementzis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dimitris Tsementzis.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix: The rules of HoTT

Appendix: The rules of HoTT

I will give the full list of rules of the system of HoTT that were visualized in the body of the paper. As in the main text I present them with “Shape” instead of “Type”. My presentation borrows elements from Kapulkin et al. (2014) and Univalent Foundations Program (2013).

1.1 Structural rules

figure aq
figure ar
figure as
figure at
figure au
figure av
figure aw
figure ax

1.2 Rules for shape constructors

1.2.1 \(\mathsf {Total}\)-shapes

figure ay
figure az
figure ba
figure bb

1.2.2 \(\mathsf {Map}\)-shapes

figure bc
figure bd
figure be
figure bf

1.2.3 \(\mathsf {Path}\)-shapes

figure bg
figure bh
figure bi
figure bj
figure bk
figure bl

1.2.4 \(\mathbf{0 }\)-shape

figure bm

1.2.5 \(\mathbf{1 }\)-shape

figure bn
figure bo

1.2.6 \(\mathbb {N}\)-shape

figure bp
figure bq
figure br
figure bs

1.3 Rules for the universes

Every rule below is instantiated for any \(i \in \omega \), whenever such an i appears.

figure bt
figure bu
figure bv
figure bw
figure bx
figure by
figure bz
figure ca
figure cb
figure cc
figure cd
figure ce
figure cf
figure cg
figure ch

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tsementzis, D. A meaning explanation for HoTT. Synthese 197, 651–680 (2020). https://doi.org/10.1007/s11229-018-02052-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11229-018-02052-1

Keywords

Search

Navigation