Abstract
The metaphor of scaffolding has become current in discussions of the cognitive help we get from artefacts, environmental affordances and each other. Consideration of mathematical tools and representations indicates that in these cases at least (and plausibly for others), scaffolding is the wrong picture, because scaffolding in good order is immobile, temporary and crude. Mathematical representations can be manipulated, are not temporary structures to aid development, and are refined. Reflection on examples from elementary algebra indicates that Menary is on the right track with his ‘enculturation’ view of mathematical cognition. Moreover, these examples allow us to elaborate his remarks on the uniqueness of mathematical representations and their role in the emergence of new thoughts.


Similar content being viewed by others
Notes
That is, the system expounded in Euclid books I–IV.
See Manders (2008) for a comprehensive analysis.
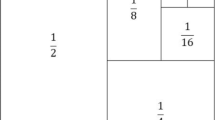
Note that a language with precise number-words that are not limited in size is already a significant cognitive tool. According to Ferreirós, “With counting, the imprecise innate grasp of cardinality is joined by a notion of order (ordinality), which refines the notion of cardinality into a precise concept, with the aid of specific words, so that they combine to obtain the number concept.” (2016, p. 186). By ‘mathematical representations’ in this paper is meant inscriptions, mental images, computer models, etc. in addition to the words for counting numbers that one has simply as a speaker of a language that expresses the counting-number concept.
Though not all of it. Following the expression-transformation rules of the language of high school algebra is not quite a perfect guarantee of rigour, because they can’t always prevent you from accidentally dividing by zero or from dividing an inequality by a negative number.
Doing philosophy of mathematical practices means treating mathematics as a human activity rather than a body of established knowledge. Whether or not this is a replacement for, a challenge to or a friend of longer established approaches to the philosophy of mathematics is matter of dispute. See Mancosu (2008, p. 18).
This does not entail that other discourses are not enculturated.
See Stone (1998) for the history of the scaffolding metaphor from its origin to 1998. See also following footnote.
Menary and others routinely present Clark as the originator of this usage in cognitive science. This is corroborated by Google Scholar searches: prior to 1976 (the year of Wood et al.), scaffolding is not mentioned in educational theory or developmental psychology. From 1976 to 1998, there are many references to scaffolding in educational theory but none in cognitive science. After 1998, scaffolding appears in papers in cognitive science, mostly with direct citations of Clark’s use. See Stone (1998) for a history of the term in educational theory from Wood et al. onwards. Writing in 1998, the year of Clark’s paper, Stone makes no mention of cognitive science. Clark does not cite Wood et al., but there is a common ancestor in Vygotsky. Wood, Bruner and Ross do not mention Vygotsky in their article but (as Stone explains) Bruner wrote on Vygotsky and in educational psychology the scaffolding metaphor was taken up as a way to articulate Vygotsky’s model of teaching as management of the pupil’s zone of proximal development. The quotation from Clark in the present paper is taken from a section in which he discusses Vygotsky with approval as a source of his own view.
Epistemic actions are “external actions that an agent performs to change his or her own computational state.” (Kirsh and Maglio, 1994, p. 514). They elaborate thus, “a physical action whose primary function is to improve cognition by: (1) reducing the memory involved in mental computation, that is, space complexity; [or] (2) reducing the number of steps involved in mental computation, that is, time complexity; [or] (3) reducing the probability of error of mental computation, that is, unreliability. Typical epistemic actions found in everyday activities… include familiar memory-saving actions such as… placing a key in a shoe, or tying a string around a finger; time-saving actions such as preparing the workplace, for example, partially sorting nuts and bolts before beginning an assembly task in order to reduce later search…; and information gathering activities such as exploring, for example, scouting unfamiliar terrain to help decide where to camp for the night.” (Op. Cit. pp. 514–515).
Chemero (1998). Of course, Clark is not responsible for what others have made of his metaphor. Nevertheless, Chemero is pertinent because the reception and use of the metaphor by the cognitive science and philosophy of mind communities is our target, rather than Clark’s personal take on it.
For the most part, the environmental affordances for mathematics are artefacts, but nothing hangs on this. One might use pebbles as counters or draw diagrams in wet sand with a stick.
Naked, because even the most rudimentary clothing is rich in affordances. With a loincloth, one might carry water, signal for help, trap a small animal, bind a wound, etc.
In his 1998 paper, Clark rejects the suggestion that the effect of mathematical training is to reprogram the brain (which he believes to be a pattern-completing, massively parallel neural net) so that it starts to behave like a serial computer. ‘Dynamic couplings’ is my gloss on Menary’s paper.
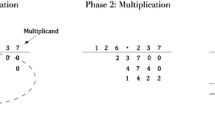
The earliest algebraic notations, such as that of Thomas Harriot, did not use brackets quite as we have them now. The methods that we now recognise as algebraic emerged in Europe from arithmetic with Hindu-Arabic numerals, and the work of brackets was done by devices such as arranging expressions in vertical columns as in long multiplication. There is some obscurity over who developed symbolic algebra first, because Renaissance mathematicians did not always publish their methods when these contravened the official standards of rigour or if they saw a commercial advantage in keeping them secret. John Wallis was convinced that Descartes must have seen and plagiarised Thomas Harriot’s book, because he heard that a French nobleman was struck by the similarity between Harriot’s system and Descartes’s. Wallis’s argument has not persuaded many historians. What matters here, philosophically, is not the origins or details of this story but how it ends, that is, with symbolic algebra governed by syntactic rules for transforming equations.
In his 1998 paper, Clark lists six kinds of help that ‘scaffolding’ can offer to help humans think, but ensuring the correctness of results is not one of them.
Reading ‘syntax’ broadly so that, for example, the rules for adding elements to diagrams in Euclidean geometry are the syntax of that system.
The use of a large, wall-hung blackboard seems to have originated at the start of the nineteenth century. Before that, mathematics was taught and learned on hand-held slates that had the same features (ease of inscription and erasure) that endear blackboards to mathematicians (Wylie 2012). The significant point here is not how or when mathematicians started using blackboards, but rather their reluctance to give them up now that other technologies are available. See Barany and MacKenzie (2014) for a fuller exploration of the place of chalk, blackboards and spontaneous inscription in mathematical practice.
See Artemeva and Fox (2011) on the persistence of ‘chalk talk’ as a pedagogical genre in university level mathematics teaching.
On the difference between expert and novice readers of mathematics, see Inglis and Alcock (2012).
See Larvor (2010, pp. 198–201) for Leibniz’s heuristic use of structural similarities between algebraic expressions.
Until the end of the sixteenth century, mathematicians tended to re-arrange equations of a given degree so that all the coefficients were positive. Perhaps a Renaissance mathematician might have seen a general relation between the number of roots and the distribution of terms either side of the equation. After all, al-Khwārizmī knew that quadratics in which squares plus numbers equal roots give two results (see Heeffer 2013). It’s not categorically impossible to understand the rule of signs without the symbolism—but no-one did.
As is common in mathematics, Galois did not invent Galois theory as it is now taught to undergraduates. The group-concept was not isolated and captured in axioms until after his death. The details of this story do not affect the philosophical point, which is that once expressed in modern notation, equations became objects of systematic mathematical enquiry. There is even a glimmer of this in Harriot, who had a classification of equations into canonical and non-canonical forms (Harriot 2007).
See Starikova (2010) for examples of the way that graph theory can supply methods to group theory via Cayley graphs. This relies on the fact that although there are often several graphs for any given finitely generated group, all the graphs of a given group share certain properties and these properties can therefore be regarded as properties of the generating group.
References
Artemeva, N., & Fox, J. (2011). The writing’s on the board: The global and the local in teaching undergraduate mathematics through chalk talk. Written Communication, 28(4), 345–379. https://doi.org/10.1177/0741088311419630.
Barany, M., & MacKenzie, D. (2014). Chalk: Materials and concepts in mathematics research. In M. Lynch & S. Woolgar (Eds.), Representation in scientific practice revisited. Cambridge: The MIT Press.
Chemero, A. (1998). ‘A stroll through the worlds of animats and humans: Review of Being there: Putting brain, body and world together again’ by Andy Clark. PSYCHE, 4(14). http://journalpsyche.org/files/0xaa4a.pdf.
Clark, A. (1998). Magic words: How language augments human computation. In P. Carruthers & J. Boucher (Eds.), Language and thought: Interdisciplinary themes (pp. 162–183). Cambridge: Cambridge University Press.
De Toffoli, S., & Giardino, V. (2013). Forms and roles of knot diagrams. Erkenntnis, 79(4), 829–842.
De Toffoli, S., & Giardino, V. (2014). An inquiry into the practice of proving in low-dimensional topology. Boston Studies in the History and the Philosophy of Science, 308, 315–336.
De Toffoli, S., & Giardino, V. (2016). Envisioning transformations. The practice of topology. In B. Larvor (Ed.), Mathematical cultures. Berlin: Springer.
Ferreirós, J. (2016). Mathematical knowledge and the interplay of practices. Princeton: Princeton University Press.
Giardino, V. (2017). «L’imagination manipulatoire en mathématique». Bulletin d’Analyse Phénoménologique [En ligne], Volume 13, Numéro 2: L’acte d’imagination: Approches phénoménologiques (Actes n°10).
Harriot, T. (2007). Artis analyticae praxis: An English translation with commentary (M. Seltman, R. Goulding, Eds., Trans.). New York: Springer.
Heeffer, A. (2013). Why the quadratic equation has only one root (according to abbaco masters). Mathematics Today, 2, 140–141.
Inglis, M., & Alcock, L. (2012). Expert and novice approaches to reading mathematical proofs. Journal for Research in Mathematics Education, 43, 358–390.
Kirsh, D., & Maglio, P. (1994). On distinguishing epistemic from pragmatic action. Cognitive Science, 18, 513–549.
Larvor, B. (2005). Proof in C17 Algebra. In Philosophia Scientiae (special issue: Fonder Autrement les Mathématiques) vol. 9. Reprinted in Perspectives on Mathematical Practices (Springer, 2007, van Kerkhove & van Bendegem (Eds.), vol. 5 of Logic, Epistemology and the Unity of Science).
Larvor, B. (2010). Syntactic analogies and impossible extensions. In B. Löwe & T. Müller (Eds.), PhiMSAMP. Philosophy of mathematics: Sociological aspects and mathematical practice (Texts in Philosophy volume 11). London: College Publications.
Mancosu, P. (2008). Editorial introduction. The philosophy of mathematical practice (pp. 1–21). Oxford: Oxford University Press.
Manders, K. (2008). The Euclidean diagram. In P. Mancosu (Ed.), The philosophy of mathematical practice (pp. 80–133). Oxford: Oxford University Press.
Menary, R. (2015). Mathematical cognition—A case of enculturation. In T. Metzinger & J. M. Windt (Eds.), Open mind: 25(T). Frankfurt am Main: MIND Group.
Pólya, G. (1954). Mathematics and plausible reasoning (Vol. 2). Princeton, NJ: Princeton University Press.
Serfati, M. (2005). La Révolution Symbolique: La Constitution de l’Ecriture Symbolique Mathématique. Preface by Jacques Bouverasse. Éditions Petra: Paris
Shulman, L. S. (2005). Signature pedagogies in the professions. Daedalus, 134(3), 52–59.
Starikova, I. (2010). Why do mathematicians need different ways of presenting mathematical objects? The case of Cayley graphs. Topoi, 29(1), 41–51.
Stone, C. A. (1998). The metaphor of scaffolding: Its utility for the field of learning disabilities. Journal of Learning Disabilities, 31(4), 344–364.
Wagner, R. (2017). Making and breaking mathematical sense: Histories and philosophies of mathematical practice. Princeton: Princeton University Press.
Wood, D., Bruner, J. S., & Ross, G. (1976). The role of tutoring in problem solving. Journal of Child Psychology and Psychiatry, 17, 89–100.
Wylie, C. D. (2012). Teaching manuals and the blackboard: Accessing historical classroom practices. History of Education, 41(2), 257–272.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Larvor, B. Why ‘scaffolding’ is the wrong metaphor: the cognitive usefulness of mathematical representations. Synthese 197, 3743–3756 (2020). https://doi.org/10.1007/s11229-018-02039-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11229-018-02039-y