Skip to main content
SpringerLink
Log in

A Sparsity Reconstruction Algorithm of Electromagnetic Tomography Technique for High Conductivity Medium Imaging

  • Research
  • Published:
Sensing and Imaging Aims and scope Submit manuscript

Abstract

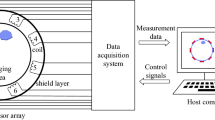
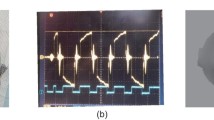
Electromagnetic tomography (EMT) is a versatile tomographic imaging technique for reconstruction of conductivity and/or permeability distribution due to the advantages of non-contact, non-intrusive, low-cost, simple structure and fast imaging. However, the ill-posed and ill-conditioned features of EMT make it difficult to obtain high quality reconstructed images. To improve the spatial resolution of the high conductivity medium imaging, the L1–L1 framework objective function is presented, which uses L1 norm as both the data fidelity term and the regularization term to weaken the influence of the data outliers and impose the sparsity feature of the measured objects. An improved Split Bregman method is proposed to solve the complicated optimization problem efficiently, which splits it into several simple sub-tasks. Each subtask can be solved by adopting the proper method. Besides, an acceleration strategy is introduced to improve the imaging speed. Numerical simulations are used to verify the effectiveness and competitive performance of the proposed improved method. The experiments are carried out by the designed modularized EMT system to further verify the effectiveness of the proposed method. The reconstructed images can precisely show the number and positions of the measured objects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  1. Wu, X., Zhao, Q., Gao, M., Xu, S., & Liu, S. (2022). Image reconstruction algorithm of electromagnetic tomography based on fractional Kalman filter. Flow Measurement and Instrumentation, 86, 102198. https://doi.org/10.1016/j.flowmeasinst.2022.102198

    Article  Google Scholar 

  2. Ma, L., & Soleimani, M. (2017). Magnetic induction tomography methods and applications: A review. Measurement Science and Technology, 28, 072001. https://doi.org/10.1088/1361-6501/aa7107

    Article  Google Scholar 

  3. Wang, C., Wang, R., Liang, X., Ye, J., & Chen, X. (2022). Design and optimization of electromagnetic tomography and electrical resistance tomography dual-modality sensor. Measurement Science and Technology, 33(10), 105120. https://doi.org/10.1088/1361-6501/ac8146

    Article  Google Scholar 

  4. Yin, W., Chen, G., Chen, L., & Wang, B. (2011). The design of a digital magnetic induction tomography (MIT) system for metallic object imaging based on half cycle demodulation. IEEE Sensors Journal, 11(10), 2233–2240. https://doi.org/10.1109/JSEN.2011.2128866

    Article  Google Scholar 

  5. Cui, Z., Chen, Y., & Wang, H. (2019). A dual-modality integrated sensor for electrical capacitance tomography and electromagnetic tomography. IEEE Sensors Journal, 19(21), 10016–10026. https://doi.org/10.1109/jsen.2019.2927629

    Article  Google Scholar 

  6. Jeon, J., Park, C., Lee, S., Chae, H., Kim, J., & Son, H. (2022). Magnetic induction tomography using multi-channel phase-domain transceiver for structural health monitoring. IEEE Transactions on Instrumentation and Measurement, 71, 4502009. https://doi.org/10.1109/TIM.2022.3151951

    Article  Google Scholar 

  7. Liu, Z., Li, W., Xue, F., Xia, F., Bu, B., & Yi, Z. (2015). Electromagnetic tomography rail defect inspection. IEEE Transactions on Magnetics, 51(10), 6201907. https://doi.org/10.1109/tmag.2015.2430283

    Article  Google Scholar 

  8. Soleimani, M. (2010). Improving the temporal resolution of magnetic induction tomography for molten metal flow visualization. IEEE Transactions on Instrumentation and Measurement, 59(3), 553–557. https://doi.org/10.1109/TIM.2009.2024704

    Article  Google Scholar 

  9. Wang, Q., Li, K., et al. (2019). Sparse defects detection and 3D imaging base on electromagnetic tomography and total variation algorithm. Review of Scientific Instruments, 90(12), 124703. https://doi.org/10.1063/1.5120118

    Article  Google Scholar 

  10. Chen, Y., Tan, C., & Dong, F. (2021). Combined planar magnetic induction tomography for local detection of intracranial hemorrhage. IEEE Transactions on Instrumentation and Measurement, 70, 4500111. https://doi.org/10.1109/tim.2020.3011621

    Article  Google Scholar 

  11. Wang, C., Guo, Q., Li, Z., & Ye, J. (2022). A new image reconstruction strategy for TMR-EMT: Combining regularization theory with guided image filtering method. Measurement Science and Technology, 33(8), 085101. https://doi.org/10.1088/1361-6501/ac5ff9

    Article  Google Scholar 

  12. Wang, H., Fedchenia, I., Shishkin, S., Finn, A., Smith, L., & Colket, M. (2015). Sparsity-inspired image reconstruction for electrical capacitance tomography. Flow Measurement and Instrumentation, 43, 59–71. https://doi.org/10.1016/j.flowmeasinst.2015.03.001

    Article  Google Scholar 

  13. Li, F., Abascal, J., Desco, M., & Soleimani, M. (2017). Total variation regularization with split bregman-based method in magnetic induction tomography using experimental data. IEEE Sensors Journal, 17(4), 976–985. https://doi.org/10.1109/jsen.2016.2637411

    Article  Google Scholar 

  14. Zhang, T., Liu, X., Zhang, W., et al. (2021). Adaptive threshold split Bregman algorithm based on magnetic induction tomography for brain injury monitoring imaging. Physiological Measurement, 42(6), 065004. https://doi.org/10.1088/1361-6579/ac05d4

    Article  Google Scholar 

  15. Tong, G., Liu, S., Chen, H., & Wang, X. (2018). Regularization iteration imaging algorithm for electrical capacitance tomography. Measurement Science and Technology, 29(3), 035403. https://doi.org/10.1088/1361-6501/aaa3c5

    Article  Google Scholar 

  16. Goldstein, T., & Osher, S. (2009). The split Bregman method for L1-regularized problems. SIAM Journal on Imaging Sciences, 2(2), 323–343. https://doi.org/10.1137/080725891

    Article  MathSciNet  Google Scholar 

  17. Liu, X., & Liu, Z. (2019). A novel algorithm based on L1-Lp norm for inverse problem of electromagnetic tomography. Flow Measurement and Instrumentation, 65, 318–326. https://doi.org/10.1016/j.flowmeasinst.2019.01.010

    Article  Google Scholar 

  18. Huang, G., Qian, W., Wang, J., Lu, W., & Peng, H. (2021). Image reconstruction based on frequency domain feature extraction for EMT. Measurement Science and Technology, 32(10), 105404. https://doi.org/10.1088/1361-6501/ac0ca6

    Article  Google Scholar 

  19. Han, M., Cheng, X., & Xue, Y. (2016). Comparison with reconstruction algorithms in magnetic induction tomography. Physiological Measurement, 37(5), 683–697. https://doi.org/10.1088/0967-3334/37/5/683

    Article  Google Scholar 

  20. Tan, C., Chen, Y., Wu, Y., Xiao, Z., & Dong, F. (2021). A modular magnetic induction tomography system for low-conductivity medium imaging. IEEE Transactions on Instrumentation and Measurement, 70, 9508708. https://doi.org/10.1109/TIM.2021.3073439

    Article  Google Scholar 

  21. Huang, G., Qian, W., Wang, J., Lu, W., & Peng, H. (2022). Image reconstruction based on sequential Monte Carlo principle for EMT. IEEE Transactions on Instrumentation and Measurement, 71, 5002914. https://doi.org/10.1109/TIM.2021.3130287

    Article  Google Scholar 

  22. Wang, J., Ma, J., Han, B., & Li, Q. (2012). Split Bregman iterative algorithm for sparse reconstruction of electrical impedance tomography. Signal Processing, 92(12), 2952–2961. https://doi.org/10.1016/j.sigpro.2012.05.027

    Article  Google Scholar 

  23. Tong, G., Liu, S., Guo, H., & Chen, H. (2019). Split Bregman iteration based image reconstruction algorithm for electrical capacitance tomography. Flow Measurement and Instrumentation, 66, 119–127. https://doi.org/10.1016/j.flowmeasinst.2019.02.003

    Article  Google Scholar 

  24. Zhao, Q., Liu, S., Chai, X., & Guo, H. (2021). A novel computational imaging algorithm based on split Bregman iterative for electrical capacitance tomography. Measurement Science and Technology, 32(12), 125401. https://doi.org/10.1088/1361-6501/ac1c1c

    Article  Google Scholar 

  25. Beck, A., & Teboulle, M. (2009). A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM Journal on Imaging Sciences, 2(1), 183–202. https://doi.org/10.1137/080716542

    Article  MathSciNet  Google Scholar 

  26. Liu, X., & Wang, Y. (2022). An improved conjugate gradient image reconstruction algorithm for electromagnetic tomography. Sensing and Imaging, 23, 5. https://doi.org/10.1007/s11220-021-00374-y

    Article  Google Scholar 

  27. Yue, Y., Liu, Z., Miao, Y., & Pan, J. (2021). 3D electromagnetic tomography using a single layer sensor array. Flow Measurement and Instrumentation, 77, 101850. https://doi.org/10.1016/j.flowmeasinst.2020.101850

    Article  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 62201511, 62003311), Scientific and technological research project in Henan Province (Nos. 222102210057, 212102210620), Key Scientific Research Project of Colleges and Universities in Henan Province (Grant No. 23A460029) and Doctoral Research Fund (No. 2020BSJJ006).

Author information

Authors and Affiliations

  1. School of Electrical and Information Engineering, Zhengzhou University of Light Industry, Zhengzhou, 450002, China

    Xianglong Liu, Danyang Li & Hangli Ren

  2. School of Mechatronics and Vehicle Engineering, Zhengzhou University of Technology, Zhengzhou, 450044, China

    Ying Wang

Authors
  1. Xianglong Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Danyang Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ying Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Hangli Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

Conceptualization: XL; Methodology: XL, DL, YW, HR; Writing-original draft preparation: XL; Writing-review and editing: DL, YW; Resources: HR.

Corresponding author

Correspondence to Xianglong Liu.

Ethics declarations

Conflict of interest

Authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, X., Li, D., Wang, Y. et al. A Sparsity Reconstruction Algorithm of Electromagnetic Tomography Technique for High Conductivity Medium Imaging. Sens Imaging 24, 12 (2023). https://doi.org/10.1007/s11220-023-00418-5

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s11220-023-00418-5

Keywords

Search

Navigation