Control of dumbbell satellite orbits using moving mass actuators

Abstract

Principles of moving mass control of the orbital parameters of an artificial dumbbell shaped satellite are discussed in the present paper. The rationale is to implement a non-jet principle of actuation by varying the geometry of the satellite through its internal degrees-of-freedom. This can be achieved by spinning the massive parts of the dumbbell and changing their relative distance upon the orbital angle according to the suggested control strategies. The control schemes aim at maintaining a desired satellite size and orientation with respect to the orbital radius in order to take advantage of the variations in the gravitational field along the elliptical orbit. The results demonstrate that the total orbital energy can follow a prescribed temporal profile by controlling the satellite orientation on the orbit to accurately track its desired target. Analytical estimates for the satellite’s energy versus the number of orbital cycles are determined from closed-form solutions. Results from both analytical estimates and numerical integration are in sufficient agreement.

Appendices

Appendix

Appendix A: Details on the governing equations.

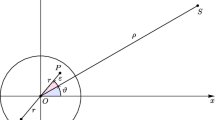
Although the derivations below are quite strightforward, they are reproduecd here due to the presence of internal degrees-of-freedom whose coordinates are varying in a prescribed way and therefore excluded from the set of generalized coordinates. With reference to Fig. 1, the gravitational potential energy and the kinetic energy of the satillate are, respectively,

$$ V = - \frac{GMm}{2}\left( {\frac{1}{{|{\mathbf{r}} + {\mathbf{l}}|}} + \frac{1}{{|{\mathbf{r}} - {\mathbf{l}}|}}} \right) $$

(A1)

and

$$ T = \frac{m}{4}\left[ {({\dot{\mathbf{r}}} + {\dot{\mathbf{l}}})^{2} + ({\dot{\mathbf{r}}} - {\dot{\mathbf{l}}})^{2} } \right] + \frac{1}{2}I\Omega^{2} , $$

(A2)

where $I = mk^{2}$ is a combined moment of inertia of rotating parts about their centers of rotation expressed through the total mass m and the radius of gyration k, $\Omega = \dot{\nu } + \dot{\theta } + \omega$ is the angular velocity, which is assumed to be the same for both of the spinning parts, and the satellite position vectors are:

$$ {\mathbf{r}} = r(\cos \nu {\mathbf{i}} + \sin \nu {\mathbf{j}}),\quad {\mathbf{l}} = l[\cos (\nu + \theta ){\mathbf{i}} + \sin (\nu + \theta ){\mathbf{j}}]. $$

(A3)

The system’s Lagrangian per unit mass is used as

$$ L = (T - V)/m. $$

(A4)

Substituting Eq. (A3) in Eqs. (A1) and (A2), conducting calculations with the Cartesian vectors, and rearranging terms brings Eq. (A4) to the form

$$ \begin{gathered} L(r,\nu ,\theta ,\dot{r},\dot{\theta }) = \frac{1}{2}(\dot{r}^{2} + r^{2} \dot{\nu }^{2} ) + \frac{1}{2}(l^{2} + k^{2} )(\dot{\nu } + \dot{\theta })^{2} + k^{2} (\dot{\nu } + \dot{\theta })\omega + \frac{1}{2}(\dot{l}^{2} + k^{2} \omega^{2} ) \hfill \\ + \frac{1}{2}GM\left( {\frac{1}{{\sqrt {r^{2} - 2lr\cos \theta + l^{2} } }} + \frac{1}{{\sqrt {r^{2} + 2lr\cos \theta + l^{2} } }}} \right). \hfill \\ \end{gathered} $$

(A5)

This Lagrangian is a function of the generalized coordinates $\{ r,\nu ,\theta \}$ and velocities $\{ \dot{r},\dot{\theta }\}$. The additive time dependent term $(\dot{l}^{2} + k^{2} \omega^{2} )/2$ does not include any state variables and thus can be removed from Eq. (A5) with no effect on the corresponding differential equations of motion. Further, taking into account the assumption $l/r < < 1$ gives

$$ \frac{1}{{\sqrt {r^{2} \pm 2lr\cos \theta + l^{2} } }} = \frac{1}{r}\left[ {1 \mp \frac{l}{r}\cos \theta + \frac{{l^{2} }}{{4r^{2} }}(1 + 3\cos 2\theta )} \right] + O\left( \frac{l}{r} \right)^{3} . $$

(A6)

Substituting (A6) in (A5) completes the derivation of Lagrangian in Eq. (2) of Sect. 2. Then Eqs. (3) through (5) follow from Euler–Lagrange equations

$$ \frac{d}{dt}\frac{\partial L}{{\partial \dot{r}}} - \frac{\partial L}{{\partial r}} = 0,\quad \frac{d}{dt}\frac{\partial L}{{\partial \dot{\nu }}} - \frac{\partial L}{{\partial \nu }} = 0,\quad \frac{d}{dt}\frac{\partial L}{{\partial \dot{\theta }}} - \frac{\partial L}{{\partial \theta }} = 0. $$

(A7)

It is seen from both Eq. (A5) and its reduced version (2) that the angular coordinate ν is cyclical, and thus the angular momentum conservation law, $\partial L/\partial \dot{\nu } = const.$, holds as

$$ r^{2} \dot{\nu } + (l^{2} + k^{2} )(\dot{\theta } + \dot{\nu }) + k^{2} \omega = const. $$

(A8)

Appendix B: Equation describing the satellite relative angle

Taking into account the assumption $k/l < < 1$ brings Eq. (5) to the form

$$ \frac{d}{dt}[l^{2} (\dot{\theta } + \dot{\nu })] + \frac{3}{2}\left( \frac{l}{r} \right)^{2} \frac{GM}{r}\sin 2\theta + k^{2} \dot{\omega } = 0. $$

(B1)

Considering the orbital angle ν as a natural independent variable and thus using the operator of time derivative, $d/dt$, from Eq. (12) gives

$$ \frac{h}{{r^{2} }}\frac{d}{d\nu }[l^{2} (\frac{h}{{r^{2} }}\frac{d\theta }{{d\nu }} + \frac{h}{{r^{2} }})] + \frac{3}{2}\left( \frac{l}{r} \right)^{2} \frac{GM}{r}\sin 2\theta = - h\frac{{k^{2} }}{{r^{2} }}\frac{d\omega }{{d\nu }}, $$

(B2)

where the quantity h is “frozen” according to Eq. (7).

Multiplying both sides of Eq. (B2) by $r^{4} /(hl^{2} )$ brings it to the form

$$ \frac{{r^{2} }}{{l^{2} }}\frac{d}{d\nu }[\frac{{l^{2} }}{{r^{2} }}(\frac{d\theta }{{d\nu }} + 1)] + \frac{3}{2}\frac{GM}{{h^{2} }}r\sin 2\theta = - \frac{{k^{2} r^{2} }}{{hl^{2} }}\frac{d\omega }{{d\nu }}. $$

(B3)

Finally, substituting the polar radius, $r = h^{2} /[GM(1 + e\cos \nu )]$, on the left-hand side of Eq. (B3) gives

$$ \frac{{d^{2} \theta }}{{d\nu^{2} }} + 2\left( {\frac{1}{l}\frac{dl}{{d\nu }} - \frac{e\sin \nu }{{1 + e\cos \nu }}} \right)\left( {\frac{d\theta }{{d\nu }} + 1} \right) + \frac{3\sin 2\theta }{{2(1 + e\cos \nu )}} = - \frac{{k^{2} r^{2} }}{{l^{2} }}\frac{d}{d\nu }\left( {\frac{1}{{r^{2} }}\frac{d\varphi }{{d\nu }}} \right) $$

(B4)

The angle φ, describing the relative position of both spinning parts, must depend upon the polar angle ν much faster than the polar radius r in order to generate a sufficient control torque. Therefore, the right-hand side of Eq. (B4) can be estimated as

$$ - \frac{{k^{2} r^{2} }}{{l^{2} }}\frac{d}{d\nu }\left( {\frac{1}{{r^{2} }}\frac{d\varphi }{{d\nu }}} \right) \approx - \frac{{k^{2} }}{{l^{2} }}\frac{{d^{2} \varphi }}{{d\nu^{2} }} $$

(B5)

Substituting (B5) in (B4) gives Eq. (16a) of Sect. 2.2. Note that the above assumption is not restrictive since, according to the control algorithm of Sect. 6, the entire right-hand side of Eq. (B4) is considered as a control input $Q(\nu )$ (se Eq. (37)). Having obtained the function $Q(\nu )$, the exact relationship can also be used for determining the dependence $\varphi = \varphi (\nu )$:

$$ - \frac{{k^{2} r^{2} }}{{l^{2} }}\frac{d}{d\nu }\left( {\frac{1}{{r^{2} }}\frac{d\varphi }{{d\nu }}} \right) = Q(\nu ). $$

(B6)

The role of control input, $Q(\nu )$, is twofold: stabilizing the satellite and changing its orientation on the orbit according to the analytically predicted law. Note that, in case of no spinning, the right-hand side of Eq. (B4) becomes zero, $Q = 0$, and the system has just one input, $l = l(\nu )$. This dependence can also be generated by a closed loop controller. The present hybrid approach however assigns the dependence $l(\nu )$ in an empirical way by selection in order to make the main controller more effective. As a guidence for such a selection, one can assume the distance $l(\nu )$ to be varying coherently with the orbital radius, for instance, as $l = l_{0} /(1 + \zeta \cos \nu )$, where $\zeta$ is a constant parameter, $|\zeta | < 1$. In this case, calculating the quantity $(dl/d\nu )/l$ and substituting the result in Eq. (B4) with zero right-hand side gives Eq. (16b) of Sect. 3.