Skip to main content
SpringerLink
Log in

Nonlinear dynamics of harmonic drive considering pitch deviation

  • Published:
Meccanica Aims and scope Submit manuscript

A Correction to this article was published on 20 March 2023

This article has been updated

Abstract

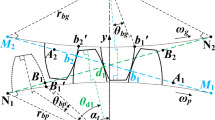
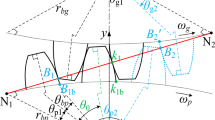
Pitch deviation as a short periodic error affects the transmission stability of harmonic drive. A measurement method is proposed to obtain the pitch deviation of a harmonic drive based on extraction of tooth profile indexing information with discrete point datum of tooth profile projection. The measured pitch deviations are introduced to a simplified nonlinear dynamic equation ignoring the flexible deformation of flexspline. The transition process of nonlinear dynamics of the system with the change of comprehensive transmission error, torque and meshing frequency are investigated and compared the dynamic characteristics with the pitch deviation to those without pitch deviation. The characteristics of neighboring periodic motions appeared in the system which affect the transmission stability are discussed. Saddle-node bifurcation, doubling periodic bifurcation and inverse doubling periodic bifurcation are found in the system and their influences on the system motion are investigated. The exploration of the dynamic characteristics of harmonic drive from the perspective of nonlinear dynamics is helpful in the selection of system parameters for improving the transmission stability of harmonic drive.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Change history

References

  1. Rached D, Fathi HG, Prasanna SG (2003) A new dynamic model of hysteresis in harmonic drives. IEEE Trans Ind Electron 50(6):1165–1171

    Article  Google Scholar 

  2. Taghirad HD, Belanger PR (1998) Modeling and parameter identification of harmonic drive systems. J Dyn Syst Meas Control 120(12):439–444

    Article  Google Scholar 

  3. Ma D, Wang R, Rao P et al (2018) Automated analysis of meshing performance of harmonic drive gears under various operating conditions. IEEE Access 6:68137–68154

    Article  Google Scholar 

  4. Hai W, Payandeh S (1997) Study of harmonic drive and design of controllers reducing torque oscillation. IFAC Proc Vol 30(20):491–496

    Article  Google Scholar 

  5. Jeon HS, Oh SH (1999) A study on stress and vibration analysis of a steel and hybrid flexspline for harmonic drive. Compos Struct 47(1–4):827–833

    Article  Google Scholar 

  6. Xu L, Zhu C, Qin L (2007) Parametric vibration for electromechanical integrated electrostatic harmonic drive. Mechatronics 17(1):31–43

    Article  MATH  Google Scholar 

  7. Xu L, Zhu C, Qin L (2007) Dynamics for an electromechanical integrated electrostatic harmonic drive. J Electrost 65:54–66

    Article  MATH  Google Scholar 

  8. Masoumi M, Alimohammadi H (2013) An investigation into the vibration of harmonic drive systems. Front Mech Eng 8(4):409–419

    Article  Google Scholar 

  9. Tjahjowidodo T, Al-Bender F, Van Brussel H (2013) Theoretical modelling and experimental identification of nonlinear torsional behaviour in harmonic drives. Mechatronics 23(5):497–504

    Article  Google Scholar 

  10. Iwasaki M, Nakamura H (2014) Vibration suppression for angular transmission errors in harmonic drive gearings and application to industrial robots. IFAC Proc Vol 47(3):6831–6836

    Article  Google Scholar 

  11. Timofeev GA, Kostikov YV (2016) Torsional rigidity of harmonic gear drives. Russ Eng Res 36(12):995–998

    Article  Google Scholar 

  12. Zhao J, Yan S, Wu J (2014) Analysis of parameter sensitivity of space manipulator with harmonic drive based on the revised response surface method. Acta Astronaut 98:86–96

    Article  Google Scholar 

  13. Yao Y, Chen X, Xing J (2020) Tooth effects on assembling bending stress of flexible tooth rim in harmonic drive. Mech Mach Theory 150:103871

    Article  Google Scholar 

  14. Hrcek S, Brumercik F, Smetanka L et al (2021) Global sensitivity analysis of chosen harmonic drive parameters affecting its lost motion. Materials 14:5057

    Article  Google Scholar 

  15. Kahraman A, Singh R (1990) Nonlinear dynamics of a spur gear pair. J Sound Vib 142(1):49–75

    Article  Google Scholar 

  16. Walha L, Fakhfakh T, Haddar M (2009) Nonlinear dynamics of a two-stage system with mesh stiffness fluctuation, bearing flexibility and backlash. Mech Mach Theory 44(5):1058–1069

    Article  MATH  Google Scholar 

  17. Shyyab A, Kahraman A (2005) Non-linear dynamic analysis of a multi-mesh gear train using multi-term harmonic balance method: sub-harmonic motions. J Sound Vib 284(1):151–172

    Article  Google Scholar 

  18. He S, Singh R, Pavic G (2008) Effect of sliding friction on gear noise based on a refined vibro-acoustic formulation. Noise Control Eng J 56(3):164–175

    Article  Google Scholar 

  19. Chang L, Cao X, He Z et al (2018) Load-related dynamic behaviors of a helical gear pair with tooth flank errors. J Mech Sci Technol 32(4):1473–1487

    Article  Google Scholar 

  20. Bai H, Song C, Zhu C (2020) Dynamic modeling and analysis of helical gear-shaft-bearing coupled system. J Theor Appl Mech 58(3):743–756

    Article  Google Scholar 

  21. Gou X, Li G, Zhu L (2022) Dynamic characteristics of a straight bevel gear drive system considering multi-state meshing and time-varying parameters. Mech Mach Theory 171:104779

    Article  Google Scholar 

  22. Zhu L, Shi J, Gou X (2020) Modeling and dynamics analyzing of a torsional-bending-pendular face-gear drive system considering multi-state engagements. Mech Mach Theory 149:103790

    Article  Google Scholar 

  23. Shi J, Gou X, Zhu L (2019) Modeling and analysis of a spur gear pair considering multi-state mesh with time-varying parameters and backlash. Mech Mach Theory 134:582–603

    Article  Google Scholar 

  24. Liu P, Zhu L, Gou X et al (2021) Modeling and analyzing of nonlinear dynamics for spur gear pair with pitch deviation under multi-state meshing. Mech Mach Theory 163:104378

    Article  Google Scholar 

  25. Liu P, Zhu L, Gou X et al (2021) Neighboring periodic motion in spur gear pair and its identification methods. Nonlinear Dyn 106:2991–3023

    Article  Google Scholar 

  26. Rhéaume FE, Champliaud H, Liu Z (2009) Understanding and modelling the torsional stiffness of harmonic drives through finite-element method. Proc Inst Mech Eng Part C J Mech Eng Sci 223:515–524

    Article  Google Scholar 

  27. Zhang Y, Pan X, Li Y et al (2022) Meshing stiffness calculation of disposable harmonic drive under full load. Machines 10(4):271

    Article  Google Scholar 

  28. Huangfu YF, Chen KK, Ma H et al (2020) Meshing and dynamic characteristics analysis of spalled gear systems: a theoretical and experimental study. Mech Syst Signal Process 139:106640

    Article  Google Scholar 

  29. GB/T 10095.1-2008/ISO 1328-1: 1995, IDT. Cylindrical gears-system of accuracy-part 1: definitions and allowable values of deviations relevant to corresponding flanks of gear teeth

  30. Deshpande L (2014) Simulation of vibrations caused by faults in bearings and gears. Ph.D. thesis, University of New South Wales, Sydney

  31. Yang JW, Sun R, Yao DC et al (2019) Nonlinear dynamic analysis of high speed multiple units gear transmission system with wear fauly. Mech Sci 10:187–197

    Article  Google Scholar 

  32. Xiang L, An CH, Zhang Y et al (2021) Failure dynamic modelling and analysis of planetary gearbox considering gear tooth spalling. Eng Fail Anal 125:105444

    Article  Google Scholar 

Download references

Acknowledgements

The authors are grateful for the financial support from Open Project of Enterprises Key Laboratory of High-performance Servo System in Guangdong Province, China (Grant No. HPSKL2021KT03), and many contributions and new ideas from Mr. Zhong Chengbo to our research in the paper.

Author information

Authors and Affiliations

  1. Enterprises Key Laboratory of High-Performance Servo System in Guangdong Province, Gree Electric Appliances, Inc. of Zhuhai, Zhuhai, 579070, China

    Zhong-fu Cheng & Li-teng Shi

  2. School of Mechanical Engineering, Tiangong University, Tianjin, 300387, China

    Jing-zhong Xing & Peng-fei Liu

Authors
  1. Zhong-fu Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Li-teng Shi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jing-zhong Xing
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Peng-fei Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jing-zhong Xing.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The original online version of this article was revised as the name of the first author was incorrectly spelled Chen instead of Cheng

Appendix

Appendix

See Tables

Table 2 Measurement datum of pitch deviation for the flexspline
Full size table

2 and

Table 3 Measurement datum of pitch deviation for the circular spline
Full size table

3.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cheng, Zf., Shi, Lt., Xing, Jz. et al. Nonlinear dynamics of harmonic drive considering pitch deviation. Meccanica 57, 2885–2902 (2022). https://doi.org/10.1007/s11012-022-01605-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11012-022-01605-6

Keywords

Search

Navigation