Study of dynamics of rotational centrifugal pendulum vibration absorbers based on tautochronic design

Abstract

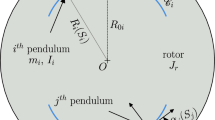
A method for designing the key parameters of rotational centrifugal pendulum vibration absorbers is proposed herein. The vibration equations of the pendulum and rotor were established by utilizing Lagrange’s equations. It was found that there were two kinds of rotational centrifugal pendulum vibration absorbers (CPVAs): a linear rotational CPVA and a nonlinear rotational CPVA, which both behaved approximately as linear oscillators. The choice of the linear rotational coefficient and the nonlinear rotational coefficient (only for the nonlinear rotational CPVA) was analyzed, and the selection of the tuning order and trajectories of the centroid of the pendulum was investigated based on tautochronic design theory. In this study, the time variables were transformed to angle variables in the vibration equations. The parameters in the equations were then non-dimensionalized, and the equations were decoupled. Finally, the vibration responses of the pendulum and rotor were solved using the harmonic balance method. The results demonstrated that the linear rotational CPVA designed by utilizing tautochronic theory provided a better damping effect than the nonlinear rotational and non-rotational CPVAs. Furthermore, the linear rotational CPVA could decrease the impact effect on the rotor by adjusting the linear rotational angle and ensure its damping performance.

Appendices

Appendix A: General path representation

In Fig. 

Fig. 7

Schematic diagram of the epicycloidal path

7, the epicycloidal path represented by a dotted line was formed by tracing the path that a perimeter point of a rolling circle of radius b produces as it rolls around a stationary circle of radius a.

φ represents the sweeping angle of the line connecting the centers of the two circles. We can obtain the equations of this epicycloid as follows:

$$ \begin{gathered} x = (a + b)\cos \varphi + b\cos \left( {\frac{a + b}{b}\varphi } \right), \hfill \\ y = (a + b)\sin \varphi + b\sin \left( {\frac{a + b}{b}\varphi } \right). \hfill \\ \end{gathered} $$

(43)

We differentiate Eq. (43) with respect to φ and obtain

$$ \begin{gathered} x{^{\prime}} = - (a + b)\sin \varphi - (a + b)\sin \left( {\frac{a + b}{b}\varphi } \right), \hfill \\ y{^{\prime}} = (a + b)\cos \varphi + (a + b)\cos \left( {\frac{a + b}{b}\varphi } \right). \hfill \\ \end{gathered} $$

(44)

The second derivative of Eq. (43) with respect to φ can be obtained as follows:

$$ \begin{gathered} x{^{\prime\prime}} = - (a + b)\cos \varphi - \frac{{(a + b)^{2} }}{b}\cos \left( {\frac{a + b}{b}\varphi } \right), \hfill \\ y{^{\prime\prime}} = - (a + b)\sin \varphi - \frac{{(a + b)^{2} }}{b}\sin \left( {\frac{a + b}{b}\varphi } \right). \hfill \\ \end{gathered} $$

(45)

The radius of curvature of this epicycloid can be obtained as follows:

$$ \rho = \frac{{[x{^{\prime 2}} + y{^{\prime 2}} ]^{\frac{3}{2}} }}{{\left| {x{^{\prime}} y{^{\prime\prime}} - x{^{\prime\prime}} y{^{\prime}} } \right|}} = \frac{4(a + b)}{{2 + \frac{a}{b}}}\cos \frac{a}{2b}\varphi . $$

(46)

The radius of curvature at the vertex can be obtained while φ = 0, as follows:

$$ \rho_{0} = \frac{4(a + b)}{{2 + \frac{a}{b}}}. $$

(47)

In Fig. 7, the angle between the tangent line at point P₂ and the negative vertical axis is represented by $\phi$, which is the sweeping angle of the radius of curvature from the initial point P₁. Since $\phi$ is a function of φ, the arc length starts from P₁ to P₂, can be expressed as

$$ S = \int_{0}^{\phi } \rho \cdot d\phi = \int_{0}^{\varphi } \rho \cdot \frac{d\phi }{{d\varphi }}d\varphi , $$

(48)

where $\phi = - \arctan ({{x{^{\prime}} } \mathord{\left/ {\vphantom {{x{^{\prime}} } {y{^{\prime}} }}} \right. \kern-\nulldelimiterspace} {y{^{\prime}} }})$. The derivative of $\phi$ with respect to φ can then be obtained as follows:

$$ \frac{d\phi }{{d\varphi }} = \frac{ - 1}{{1 + \left( {\frac{{x{^{\prime}} }}{{y{^{\prime}} }}} \right)^{2} }}\frac{{d\left( {\frac{{x{^{\prime}} }}{{y{^{\prime}} }}} \right)}}{d\varphi }, $$

(49)

where

$$ \frac{1}{{1 + \left( {\frac{{x{^{\prime}} }}{{y{^{\prime}} }}} \right)^{2} }} = \frac{{\left[ {\cos \varphi + \cos \left( {\frac{a + b}{b}\varphi } \right)} \right]^{2} }}{{\left[ {2\cos \left( {\frac{a}{2b}\varphi } \right)} \right]^{2} }},{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{d\left( {\frac{{x{^{\prime}} }}{{y{^{\prime}} }}} \right)}}{d\varphi } = - \frac{{\left( {1 + \frac{a + b}{b}} \right) \cdot 2\cos^{2} \left( {\frac{a}{2b}\varphi } \right)}}{{\left[ {\cos \varphi + \cos \left( {\frac{a + b}{b}\varphi } \right)} \right]^{2} }}. $$

(50)

The expression of S can be obtained as follows:

$$ S = \frac{4b(a + b)}{a}\sin \left( {\frac{a}{2b}\varphi } \right). $$

(51)

Therefore, the equation relating ρ and S can be obtained as follows:

$$ \rho_{0}^{2} - \rho^{2} = \lambda^{2} S^{2} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda = \frac{a}{a + 2b}{\kern 1pt} {\kern 1pt} . $$

(52)

If a = 0, then λ² = 0, the rolling circle actually rolls on a fixed point, and the trace becomes a circle. However, if a = ∞, then λ² = 1, the rolling circle actually rolls on a straight line, and the trace becomes a cycloid. The other values of λ within the lower and upper boundaries of 0 and 1 cause the paths to become epicycloids, but only a special value provides the tautochrone.

In Fig. 8, the angles between the tangent line of any point on the trace and horizontal axis are represented by $\phi$. The expression of $\phi$ can be obtained using Eq. (52), as follows:

$$ \phi = \int_{0}^{\phi } {d\phi } = \int_{0}^{s} {\frac{dS}{\rho } = } \int_{0}^{s} {\frac{dS}{{\sqrt {\rho_{0}^{2} - \lambda^{2} S^{2} } }} = } \frac{1}{\lambda }\arcsin \frac{\lambda S}{{\rho_{0} }}. $$

(53)

Fig. 8

Representation of the trajectory of the centroid of the pendulum

The relationships between the parameters in Eq. (53) are shown in Fig. 9, where

$$ \rho = \rho_{0} \cos \lambda \phi . $$

(54)

Fig. 9

Relationship between ρ, ρ₀, λ, $\phi$, and S

The coordinate of the centroid of the pendulum in Fig. 8 can be expressed as

$$ \begin{aligned} &x = \int_{0}^{S} {\cos \phi } dS = \int_{0}^{\phi } {\cos \phi } \rho d\phi = \int_{0}^{\phi } {\rho_{0} \cos \phi } \cos (\lambda \phi )d\phi , \hfill \\ &y = - C + \int_{0}^{S} {\sin \phi } dS = - C + \int_{0}^{\phi } {\sin \phi } \rho d\phi = - C + \int_{0}^{\phi } {\rho_{0} \sin \phi } \sin (\lambda \phi )d\phi . \hfill \\ \end{aligned} $$

(55)

If λ ≠ 1, we can obtain

$$ \begin{aligned} x & = \frac{{\rho_{0} }}{{1 - \lambda^{2} }}\left[ {\sin \phi \cos (\lambda \phi ) - \frac{{\lambda^{2} S}}{{\rho_{0} }}\cos \phi } \right], \\ y & = - C - \frac{{\rho_{0} }}{{1 - \lambda^{2} }}\left[ {\cos \phi \cos (\lambda \phi ) + \frac{{\lambda^{2} S}}{{\rho_{0} }}\sin \phi - 1} \right]. \\ \end{aligned} $$

(56)

The square of the distance between the centroid of the pendulum and the center of rotor can be expressed as

$$ \begin{aligned} R_{p}^{2} & = x^{2} + y^{2} \\ & = C^{2} + A^{2} \left[ {\cos^{2} (\lambda \phi ) - 2\cos \phi \cos (\lambda \phi ) - 2\frac{{\lambda^{2} S}}{{\rho_{0} }}\sin \phi + \frac{{\lambda^{4} S^{2} }}{{\rho_{0}^{2} }} + 1} \right] \\ & \quad + 2CA\left[ {\cos \phi \cos (\lambda \phi ) + \frac{{\lambda^{2} S}}{{\rho_{0} }}\sin \phi - 1} \right],\;{\kern 1pt} A = \frac{{\rho_{0} }}{{1 - \lambda^{2} }} \\ \end{aligned} $$

(57)

According to tuning theory, $\sqrt {{{(C - \rho_{0} )} \mathord{\left/ {\vphantom {{(C - \rho_{0} )} {\rho_{0} }}} \right. \kern-\nulldelimiterspace} {\rho_{0} }}} { = }n$, and therefore, $C = \rho_{0} (n^{2} + 1)$. The substitution of Eq. (57) into Eq. (11) in the main text leads to the condition of the tautochrone of the epicycloid:

$$ A = C,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda^{2} = \lambda_{e1}^{2} = \frac{{n^{2} }}{{n^{2} + 1}}. $$

(58)

Furthermore, it can be proven that the center of the stationary circle coincides with the center of the rotor if Eq. (58) is satisfied [8].

Appendix B: Equations of cutouts of rotational CPVA

Figure 10 shows the schematic diagram of a rotating pendulum, in which (0, −C) represents the vertex of the trajectory of the centroid of the pendulum, and H and D represent the distances from the centers of the rollers at the initial point (β = 0) to the vertical and horizontal axes, respectively. If the radius of the roller is a_r, the vertices of the cutouts on the rotor can be represented by (−H, −D−a_r) and (H, −D−a_r), respectively. (x_b1, y_b1) and (x_b2, y_b2) represent the vertices of the cutouts on the pendulums, respectively, (x_E, y_E) represents the midpoint of the line connecting (x_b1, y_b1) and (x_b2, y_b2), and (x_r1, y_r1) and (x_r2, y_r2) represent the centers of the two rollers. The left cutout curves on the rotor and pendulum can be expressed by C₁ and C₂, respectively.

Fig.10

Schematic diagram of the rotating CPVA

Now that the coordinates of the centroid of the pendulum can be expressed by Eq. (56), according to the structural relations, the coordinate of (x_E, y_E) can be obtained as follows:

$$ \begin{aligned} x_{E} =& x + (D - C - a_{r} )\sin \beta = \frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\sin \phi \cdot \cos (\lambda \phi ) \\&- \lambda \sin (\lambda \phi ) \cdot \cos \phi ] + (D - C - a_{r} )\sin \beta ,\\ y_{E} =& y - (D - C - a_{r} )\cos \beta = - C\\ &- \frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\cos \phi \cdot \cos (\lambda \phi ) + \lambda \sin (\lambda \phi )\sin \phi - 1] \\&- (D - C - a_{r} )\cos \beta . \end{aligned} $$

(59)

Since point E is located at the middle of the line connecting (x_b1, y_b1) and (x_b2, y_b2), the coordinates of point b₁ can be expressed as

$$ \begin{aligned} x_{b1} =& x_{E} - H\cos \beta = \frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\sin \phi \cdot \cos (\lambda \phi ) \\&- \lambda \sin (\lambda \phi ) \cdot \cos \phi ] + (D - C - a_{r} )\sin \beta \\&- H\cos \beta , \\ y_{b1} =& y_{E} - H\sin \beta = - C - \frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\cos \phi \cdot \cos (\lambda \phi )\\ &+ \lambda \sin (\lambda \phi )\sin \phi - 1] - (D - C - a_{r} )\cos \beta\\ &- H\sin \beta . \end{aligned} $$

(60)

Similarly, (x_r1, y_r1) is located at the middle of the line connecting (x_b1, y_b1) and (− H, − D − a_r), and therefore,

$$ \begin{gathered} x_{r1} = \frac{1}{2}(x_{b1} - H) = \frac{1}{2}\left\{ {\frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\sin \phi \cdot \cos (\lambda \phi ) - \lambda \sin (\lambda \phi ) \cdot \cos \phi ] + (D - C - a_{r} )\sin \beta - H\cos \beta - H} \right\}, \hfill \\ y_{r1} = \frac{1}{2}(y_{b1} - D - a_{r} ) = \frac{1}{2}\left\{ { - C - D - a_{r} - \frac{{\rho_{0} }}{{1 - \lambda^{2} }}[\cos \phi \cdot \cos (\lambda \phi ) + \lambda \sin (\lambda \phi )\sin \phi - 1] - (D - C - a_{r} )\cos \beta - H\sin \beta } \right\}. \hfill \\ \end{gathered} $$

(61)

In Fig. 10, supposing that the angle between the tangent line at any point on the left cutout on the rotor and the horizontal axis is represented by $\phi_{1}$, then the curve C₁ can be expressed as

$$ x_{1} = x_{r1} + a_{r} \sin \phi_{1} ,{\kern 1pt} {\kern 1pt} y_{1} = y_{r1} - a_{r} \cos \phi_{1} ,{\kern 1pt} {\kern 1pt} \phi_{1} = \arctan \left( {\frac{{{{\partial y_{r1} } \mathord{\left/ {\vphantom {{\partial y_{r1} } {\partial S}}} \right. \kern-\nulldelimiterspace} {\partial S}}}}{{{{\partial x_{r1} } \mathord{\left/ {\vphantom {{\partial x_{r1} } {\partial S}}} \right. \kern-\nulldelimiterspace} {\partial S}}}}} \right). $$

(62)

We differentiate Eq. (61) with respect to S and obtain

$$ \begin{gathered} \frac{{\partial x_{r1} }}{\partial S} = \frac{1}{2}\left\{ {\cos \phi + [(D - C - a_{r} )\cos \beta + H\sin \beta ]\frac{\partial \beta }{{\partial S}}} \right\}, \hfill \\ \frac{{\partial y_{r1} }}{\partial S} = \frac{1}{2}\left\{ {\sin \phi + [(D - C - a_{r} )\sin \beta - H\cos \beta ]\frac{\partial \beta }{{\partial S}}} \right\}. \hfill \\ \end{gathered} $$

(63)

$\phi_{1}$ in Eq. (62) can be expressed as

$$ \phi_{1} = \hbox{arc}\,\hbox{tan}\,\frac{{\sin \phi + [(D - C - a)\sin \beta - H\cos \beta ]\frac{\partial \beta }{{\partial S}}}}{{\cos \phi + [(D - C - a)\cos \beta + H\sin \beta ]\frac{\partial \beta }{{\partial S}}}}. $$

(64)

Therefore, $\sin \phi_{1}$ and $\cos \phi_{1}$ in Eq. (62) can be expressed as

$$ \begin{gathered} \sin \phi_{1} = \frac{{\sin \phi + [(D - C - a_{r} )\sin \beta - H\cos \beta ]\frac{\partial \beta }{{\partial S}}}}{{\sqrt {1 + [(D - C - a)^{2} + H^{2} ](\frac{\partial \beta }{{\partial S}})^{2} + 2[(D - C - a_{r} )\cos (\beta - \phi ) + H\sin (\beta - \phi )]\frac{\partial \beta }{{\partial S}}} }}, \hfill \\ \cos \phi_{1} = \frac{{\cos \phi + [(D - C - a_{r} )\cos \beta + H\sin \beta ]\frac{\partial \beta }{{\partial S}}}}{{\sqrt {1 + [(D - C - a)^{2} + H^{2} ](\frac{\partial \beta }{{\partial S}})^{2} + 2[(D - C - a_{r} )\cos (\beta - \phi ) + H\sin (\beta - \phi )]\frac{\partial \beta }{{\partial S}}} }}. \hfill \\ \end{gathered} $$

(65)

Substitution of Eq. (65) into Eq. (62) yields the equation of C₁ without $\phi_{1}$. In the general structural design of the CPVA, curve C₂ is regarded as anti-symmetric with curve C₁ about the center of the roller. Therefore, if the centroid of the pendulum is located at (0, −C), the curve C₂ is anti-symmetric with the curve C₁ about (−H, −D), and the expression of C₂ at the initial point can also be obtained:

$$ x_{2} = - 2H - x_{1} ,{\kern 1pt} {\kern 1pt} y_{2} = - 2D - y_{1} . $$

(66)

The right cutouts on the rotor and pendulum can also be obtained using the symmetric property.

If β = 0, then $\phi_{1} = \phi$, and Eqs. (62) and (66) become equations describing the cutouts on the rotor and pendulum of the non-rotational CPVA system, respectively.