Skip to main content
SpringerLink
Log in

Finding the hole in a wall

  • Original Paper
  • Published:
Journal of Mathematical Chemistry Aims and scope Submit manuscript

Abstract

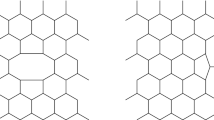
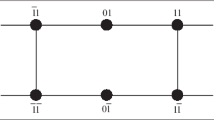
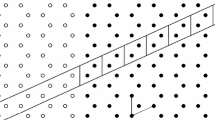
In this paper we model a graphene nano-ribbon structure by analysing an infinite 3-regular hexagonal grid which is transformed to a rectangular coordinate system or “wall”. Our goal is to solve the inverse problem of identifying the position of a single vacancy break using the lengths of the closed paths along the edges of the underlying graph. We provide an algorithm to determine the exact position of the defect by using data from at most three reference points.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

Code availability

Python code available on request.

References

  1. F. Banhart, J. Kotakoski, A.V. Krashaninnikov, Structual defects in graphene. Am. Chem. Soc. 5(1), 26–41 (2011). https://doi.org/10.1021/nn102598m

    Article  CAS  Google Scholar 

  2. M. Manoharan, H. Mizuta, Point defect-induced transport bandgap widening in the downscaled armchair graphene nanoribbon device. Carbon 64, 416–423 (2013). https://doi.org/10.1016/j.carbon.2013.07.094

    Article  CAS  Google Scholar 

  3. I. Shtepliuk, R. Yakimova, Interband transitions in closed-shell vacancy containing graphene quantum dots complexed with heavy metals. Phys. Chem. Chem. Phys. 20, 21528–21543 (2018). https://doi.org/10.1039/C8CP03306D

    Article  CAS  PubMed  Google Scholar 

  4. P. Exner, Contact interactions on graph superlattices. J. Phys. A: Math. Gen. 29, 87–102 (1996). https://doi.org/10.1088/0305-4470/29/1/011

    Article  CAS  Google Scholar 

  5. J. Griffith, A free-electron theory of conjugated molecules I. Polycyclic hydrocarbons. Trans. Faraday Soc. 49, 345–351 (1953). https://doi.org/10.1039/TF9534900345

    Article  CAS  Google Scholar 

  6. B. Gutkin, U. Smilansky, Can one hear the shape of a graph? J. Phys. A: Math. Gen. 34, 6061–6068 (2001). https://doi.org/10.1088/0305-4470/34/31/301

    Article  Google Scholar 

  7. P. Kuchment, Graph models for waves in thin structures. Waves Random Media 12, R1–R24 (2002). https://doi.org/10.1088/0959-7174/12/4/201

    Article  Google Scholar 

  8. P. Kurasov, M. Nowaczyk, Inverse spectral problem for quantum graphs. J. Phys. A: Math. Gen. 38, 4901–4915 (2005). https://doi.org/10.1088/0305-4470/38/22/014

    Article  Google Scholar 

  9. K. Pankrashkin, Spectra of Schrödinger operators on equilateral quantum graphs. Lett. Math. Phys. 77, 139–154 (2006). https://doi.org/10.1007/s11005-006-0088-0

    Article  Google Scholar 

Download references

Funding

This material is based upon work supported by the National Research Foundation under Grant Numbers 89147 and 103530.

Author information

Authors and Affiliations

  1. School of Mathematics, University of the Witwatersrand, Private Bag 3, P O WITS, Johannesburg, 2050, South Africa

    M. Archibald & S. Currie

  2. Faculty of Applied Mathematics, AGH University of Science and Technology, al. A. Mickiewicza 30, 30-059, Krakow, Poland

    M. Nowaczyk

Authors
  1. M. Archibald
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Currie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Nowaczyk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Currie.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Archibald, M., Currie, S. & Nowaczyk, M. Finding the hole in a wall. J Math Chem 58, 2313–2323 (2020). https://doi.org/10.1007/s10910-020-01178-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10910-020-01178-3

Keywords

Mathematics Subject Classification

Search

Navigation