Skip to main content
SpringerLink
Log in

Wave scattering by Pi-type breakwater floating in deep water

  • Published:
Journal of Engineering Mathematics Aims and scope Submit manuscript

Abstract

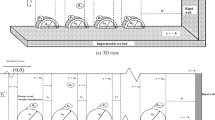
This article presents a study on surface gravity wave scattering by a rectangular (box-type) breakwater with thin side plates in the situation of oblique incident waves in deep water. Applying the continuity of fluid pressure and velocity to Havelock’s expansion of velocity potentials, the problem is converted to an integral equation of the Fredholm type, whose solution is the horizontal component of fluid velocity. The integral equation is solved by employing Galerkin’s approximation with polynomials as basis functions multiplied by suitable weight functions. The wave reflection and transmission coefficients are calculated numerically to find the breakwater’s performance on wave scattering. The accuracy of the results is verified through numerical convergence and checking of the energy balance equation. The rectangular breakwater reflects long waves to some extent in water of infinite depth, in contrast to a thin breakwater. The thin plates attached to the rectangular breakwater show a reduction in wave transmission. Furthermore, the attachment of thin plates leads to an increment in horizontal force and a reduction in vertical force.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Ursell F (1947) The effect of a fixed vertical barrier on surface waves in deep water. Math Proc Camb Philos Soc 43(3):374–382

    Article  MathSciNet  MATH  Google Scholar 

  2. Evans DV (1970) Diffraction of water waves by a submerged vertical plate. J Fluid Mech 40(3):433–451

    Article  MATH  Google Scholar 

  3. Tuck EO (1971) Transmission of water waves through small apertures. J Fluid Mech 49(1):65–74

    Article  MATH  Google Scholar 

  4. Porter D (1972) The transmission of surface waves through a gap in a vertical barrier. Math Proc Camb Philos Soc 71(2):411–421

  5. Mandal BN, Kundu PK (1986) Scattering of water waves by vertical barriers and associated mathematical methods. Proc Indian Nat Sci Acad Part A 53:514–530

  6. Chakrabarti A, Banerjea S, Mandal BN, Sahoo T (1997) A unified approach to problems of scattering of surface water waves by vertical barriers. J Austral Math Soc Ser B 39(1):93–103

    Article  MathSciNet  MATH  Google Scholar 

  7. Chakrabarti A, Manam SR, Banerjea S (2003) Scattering of surface water waves involving a vertical barrier with a gap. J Eng Math 45:183–194

    Article  MathSciNet  MATH  Google Scholar 

  8. McIver P (1985) Scattering of water waves by two surface-piercing vertical barriers. IMA J Appl Math 35(3):339–355

    Article  MathSciNet  MATH  Google Scholar 

  9. De S, Mandal BN, Chakrabarti A (2009) Water-wave scattering by two submerged plane vertical barriers—Abel integral equation approach. J Eng Math 65:75–87

    Article  MathSciNet  MATH  Google Scholar 

  10. De S, Mandal BN, Chakrabarti A (2010) Use of Abel integral equations in water wave scattering by two surface-piercing barriers. Wave Motion 47(5):279–288

    Article  MathSciNet  MATH  Google Scholar 

  11. Mei CC, Black JL (1969) Scattering of surface waves by rectangular obstacles in waters of finite depth. J Fluid Mech 38(3):499–511

    Article  MATH  Google Scholar 

  12. Bai KJ (1975) Diffraction of oblique waves by an infinite cylinder. J Fluid Mech 68(3):513–535

    Article  MATH  Google Scholar 

  13. Kanoria M, Dolai DP, Mandal BN (1999) Water-wave scattering by thick vertical barriers. J Eng Math 35:361–384

    Article  MathSciNet  MATH  Google Scholar 

  14. Drimer N, Agnon Y, Stiassnie M (1992) A simplified analytical model for a floating breakwater in water of finite depth. Appl Ocean Res 14(1):33–41

    Article  Google Scholar 

  15. Abul-Azm AG, Gesraha MR (2000) Approximation to the hydrodynamics of floating pontoons under oblique waves. Ocean Eng 27(4):365–384

    Article  Google Scholar 

  16. Manisha, Kaligatla RB, Sahoo T (2019) Effect of bottom undulation for mitigating wave-induced forces on a floating bridge. Wave Motion 89:166–184

    Article  MathSciNet  MATH  Google Scholar 

  17. Das BC, De S, Mandal BN (2020) Oblique water waves scattering by a thick barrier with rectangular cross section in deep water. J Eng Math 122:81–99

    Article  MathSciNet  MATH  Google Scholar 

  18. Koutandos E, Prinos P, Gironella X (2005) Floating breakwaters under regular and irregular wave forcing: reflection and transmission characteristics. J Hydraul Res 43(2):174–188

    Article  Google Scholar 

  19. Koftis TH, Prinos P, Koutandos E (2006) 2D-V hydrodynamics of wave-floating breakwater interaction. J Hydraul Res 44(4):451–469

    Article  Google Scholar 

  20. Gesraha MR (2006) Analysis of \(\Pi \) shaped floating breakwater in oblique waves: I. Impervious rigid wave boards. Appl Ocean Res 28(5):327–338

    Article  Google Scholar 

  21. Ruol P, Martinelli L, Pezzutto P (2003) Formula to predict transmission for \(\uppi \)-type floating breakwaters. J Waterw Port Coast Ocean Eng 139(1):1–8

    Article  Google Scholar 

  22. Mandal BN, Chakrabarti A (2000) Water wave scattering by barriers. Wit Pr/Computational Mechanics

  23. Linton CM, McIver P (2001) Handbook of mathematical techniques for wave/structure interactions. CRC Press, Boca Raton

    Book  MATH  Google Scholar 

  24. Havelock TH (1929) Forced surface-waves on water. Lond Edinb Dublin Philos Mag J Sci 8(51):569–576

    Article  MATH  Google Scholar 

  25. Parsons NF, Martin PA (1992) Scattering of water waves by submerged plates using hypersingular integral equations. Appl Ocean Res 14:313–321

    Article  Google Scholar 

  26. Porter R, Evans DV (1995) Complementary approximations to wave scattering by vertical barriers. J Fluid Mech 294:155–80

    Article  MathSciNet  MATH  Google Scholar 

  27. Evans DV, Fernyhough M (1995) Edge waves along periodic coastlines. Part 2. J Fluid Mech 297:307–25

    Article  MathSciNet  MATH  Google Scholar 

  28. Das BC, De S, Mandal BN (2018) Oblique wave scattering by thin vertical barriers in deep water: solution by multi-term Galerkin technique using simple polynomials as basis. J Mar Sci Technol 23:915–925

    Article  Google Scholar 

Download references

Acknowledgements

The authors thank the reviewers for their comments and suggestions to revise the paper in the present form. This work is carried out with the funding support of Science and Engineering Research Board, Government of India under MATRICS project with grant No. MTR/2022/000113.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computing, Indian Institute of Technology (ISM) Dhanbad, Dhanbad, 826004, India

    R. B. Kaligatla & S. Singh

  2. Physics and Applied Mathematics Unit, Indian Statistical Institute, 203, B.T. Road, Kolkata, 700108, India

    B. N. Mandal

Authors
  1. R. B. Kaligatla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. S. Singh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. B. N. Mandal
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

RBK: Problem formulation, Derivations, Investigation, Editing; SS: Derivations, Computations, Manuscript preparation; BNM: Method construction, Supervision; All authors reviewed the manuscript.

Corresponding author

Correspondence to R. B. Kaligatla.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kaligatla, R.B., Singh, S. & Mandal, B.N. Wave scattering by Pi-type breakwater floating in deep water. J Eng Math 143, 7 (2023). https://doi.org/10.1007/s10665-023-10301-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s10665-023-10301-7

Keywords

Search

Navigation