Can Building Subway Systems Improve Air Quality? New Evidence from Multiple Cities and Machine Learning

Abstract

Public investments in subway systems are often motivated by improving local air quality. Recent studies, however, have reached different conclusions on the air quality benefits of subway investment. To reconcile these findings, this paper examines the air quality effects of all 359 subway line openings in China between 2013 and 2018. The machine learning method adopted in this paper substantially improves the consistency and precision of the estimates by purging seasonality, volatility, and the nonlinear effects of meteorological conditions in air quality data. The empirical results suggest an insignificant short-term effect and a significant long-term effect, which is expected as the adjustment of commuting mode takes time. Using the causal forest approach, the heterogeneity analysis find that a city that is experiencing rapid economic growth from a lower income level and currently has fewer subway lines is more likely to experience statistically significant improvements in air quality from a subway opening. These findings help reconcile the different findings in the literature and shed light on air pollution reduction as one of the objectives of public transit investment.

Appendices

Appendix A

The Fig.

Fig. 6

Policy Interventions and Predicted AQI. Panel a Predicted AQI in Beijing. Panel b Predicted AQI in Shanghai

6 shows the predicted AQI in Beijing and Shanghai as well as policy interventions, indicated by the vertical lines. For Beijing, the policies are,

• (1) Implementation of Beijing Air Pollution Prevention and Control Regulations. (2014/1/22)

• (2) APEC Leaders' 8th Informal Meeting (2014/11/3).

• (3) Anti-fascist Parades (2015/9/3).

• (4) Implementation of Beijing Stage 6 "Gasoline for Vehicles" (DB11/238-2016) and "Diesel for Vehicles" (DB11/239-2016) standards (2017/1/1).

• (5) Intensive inspection of the Blue-sky Defense Campaign (2018/6/11).

For Shanghai, the policies are:

• (1) Implementation of Emergency Plan for Heavy Air Quality Pollution (2013/12/1).

• (2) Prohibiting vehicles according to the National II standard (GB 18352.2) (2016/1/1).

• (3) Regional Air Pollution Prevention and Control Cooperation Group meeting held (2014/4/21).

• (4) National Environmental Protection Inspection (2016/11/28).

• (5) National Environmental Protection Inspection Review Works (huitoukan) (2018/5/31).

As an example, the first red line in Panel (a) refers to January 22, 2014, which is the date of the implementation of Beijing air pollution prevention and control regulations. The regulations set standards for air quality, as well as emission control standards and industry governance measures. These measures tend to reduce air pollution. The blue line in Panel (a) shows a rapid decline in AQI after that day. The other events reported in Fig. 6 are similar to the example. The figure indicates that air quality improved during these events and that the magnitude of the improvements varied across events. The air quality improvements that we detect help validate the model and suggest that the predicted air pollution data is sensitive to non-weather shocks (Fig. 

Fig. 7

CATEs of Subway Opening on PM2.5 by the Minimum Distance between Subway and Air Pollution Monitor

7).

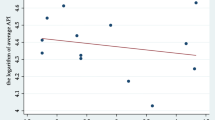
This figure shows how the conditional average treatment effects (CATEs) vary with the minimum distance between the subway and air pollution monitor. CATEs are estimated using causal forest algorithms (Tables 

Table 9 New subway lines opened between 2013 and 2018 in Mainland China

9,

Table 10 Effects of subway opening on other air pollutants

10,

Table 11 Estimation of the effects of subway openings using alternative time trends

11,

Table 12 Subway lines whose opening was delayed due to exogenous factors

12,

Table 13 Factors mainly driving the splitting of causal forest

13 and

Table 14 Conditional average treatment effects group of interest

14). The outcome variable was predicted PM2.5, and the covariates are those listed in Fig. 4.

Appendix B

2.1 An Illustrative Example of Predicting the AQI

To predict the counterfactual Air Quality Index (AQI), we train a random forest model to fit air pollution with predictors, where $\widehat{AQI}=f(meteorological, temporal,human)$.

• 1. To calculate the expectation, we randomly assign meteorological and temporal factors and conduct counterfactual predictions using the trained model, obtaining the counterfactual AQI for each random assignment, denoted as ${\widehat{AQI}}_{random1}^{Jan 1st 2010}=f({meteorological}_{random1},{ temporal}_{random1},{human}^{Jan 1st 2010})$

• 2. Repeating the second step 1000 times, we obtain ${\widehat{AQI}}_{random300}^{Jan 1st 2010}=f({meteorological}_{random300},{ temporal}_{random300},{human}^{Jan 1st 2010})$. We then consider the average of the predicted outcomes, ${\overline{\widehat{AQI}} }^{Jan 1st 2010}$ as the predicted AQI. This predicted AQI is the counterfactual AQI if the meteorological and temporal factors are typical on that day.

Appendix C

3.1 Methods of Calculating Standard Errors

In the two-stage method we employ, uncertainty arises from both the prediction and regression steps, and currently, there is no established guideline for calculating standard errors in this context.

In the main text, we utilize the bootstrap method to calculate standard errors, considering only the uncertainty from the second step. Theoretically, considering the uncertainty from the first step could lead to a larger standard error. Since our baseline result indicates an insignificant effect, this conclusion remains robust even with a potentially larger standard error.

To further affirm the robustness, following the approach suggested by Burlig et al. (2020), we attempt to capture uncertainty from both steps by employing a bootstrap method. Unfortunately, we find that performing the bootstrap is not feasible. As an alternative, we opt to conduct the robustness check using the residual approach (Burlig et al. 2020).

We employ the following procedure: First, for each air quality monitor, we sample N observations with replacement (where N equals the original number of observations). We then train the random forest model using bootstrapped data and obtain the residual ($y-\widehat{y}$). We repeat these steps 20 times. Next, we should sample the data from step one with replacement, generate multiple subsamples, estimate treatment effects using these subsamples, and calculate the standard deviation as the bootstrapped standard error. However, the data obtained from step one is substantial, estimated at approximately 400 GB (20 GB for the baseline dataset * sampled 20 times), exceeding the computer’s available memory for processing. Therefore, we opt for an approximate estimation. In the approximation, we exclusively employ the Air Quality Index (AQI) as the dependent variable, disregarding other indices of pollutants and restricting our analysis to the subsample representing the first occurrence of a subway opening in a city. To ensure comparability, we also apply similar approximations to the cluster regressions used for comparison. The estimates and standard errors may deviate from the baseline, primarily because we use subsamples instead of the full sample, leading to a reduction in the number of observations.

As demonstrated in Table 

Table 15 Effects of subway openings on AQI (bootstrap)

15 we observe that the standard errors, accounting for prediction errors from the first step, are quantitatively similar (albeit slightly larger) to the standard errors that only include the uncertainty from the second step. Given our assertion of an insignificant effect in the baseline estimation, a slightly larger standard error further reinforces the robustness of our baseline results.

Considering both the theoretical analysis and the bootstrap results of the residual approach, we believe that the issue of uncertainty from the first step may not pose a significant threat to our baseline results.