Skip to main content
SpringerLink
Log in

Bayesian model construction based on data-experts oriented approaches for assessing the phosphate effluents effects

  • Published:
Applied Intelligence Aims and scope Submit manuscript

Abstract

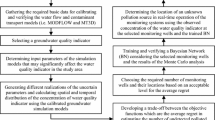
In the near future, it is estimated that our world would attend a war over waters. Whereas, the effluents of the laundry of phosphate damages more and more the watershed in mining areas. The analysis of these impacts is in fact a crucial task for the preservation of the area’s water resources. In this paper, we introduced a hybrid approach-based Bayesian network model construction for assessing the phosphate laundry effluents effects. We proposed a novel discrete Bayesian Network model which is built using a hybrid approach based on Expert and data-oriented methods for structure learning. Our aim is to propose a novel data-oriented method for resolving the Bayesian network (BN) structure learning that will be improved basing on the experts’ knowledge for efficient modelling of the cause-effect relationships. And then the parameters learning procedure is performed basing on the Expectation Maximization algorithm (EM). The evaluation of the proposed data-oriented method based on two well-known benchmarking BNs demonstrates the superiority of the proposed method in terms of BN structure evaluation metrics (i.e. structure difference, correct edges, added edges, reversed edges and deleted edges). The proposed BN model allows the assessment of the groundwater quality taking into consideration several chemical factors and influencers on the absorption of discharged metals. Depending on a real collected water samples from the Gafsa phosphatic areas (southwestern Tunisia), we built the BN model which permits the analysis of different basic physico-chemical variables and its dependencies. Moreover, the generated results illustrate that our technique has higher performance compared with the other Bayesian techniques.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Pradhan S (2017) Water war thesis: a myth or a reality. Int J Arts Humanit Soc Sci 2:12–15

    Google Scholar 

  2. Freedman B, Hutchinson TC (1981) Sources of metal and elemental contaminants of terrestrial environments. In: Lepp NW (ed) Effect of heavy metal pollution on plants. Metals in the environment, vol. II. London and New Jersey, p 35–94

  3. Webber (1981) Trace metals in agriculture. In: Lepp NW (ed) Effect of heavy metal pollution on plants. Metals in the environment, vol. II. London and New Jersey, p 159–184

  4. Marzougui S, Sdiri A, Rekhiss F (2016) Heavy metals’ mobility from phosphate washing effluents discharged in the Gafsa area (southwestern Tunisia). Arab J Geosci 9(12):599

    Article  Google Scholar 

  5. Yang Z, Yang Z, Yin J (2018) Realising advanced risk-based port state control inspection using data-driven Bayesian networks. Transp Res A Policy Pract 110:38–56

    Article  Google Scholar 

  6. Cano A, Masegosa AR, Moral S (2011) A method for integrating expert knowledge when learning Bayesian networks from data. IEEE Trans Syst Man Cybern Part B (Cybernetics) 41(5):1382–1394

    Article  Google Scholar 

  7. Yet B, Perkins Z, Fenton N, Tai N, Marsh W (2014) Not just data: A method for improving prediction with knowledge. J Biomed Inform 48:28–37

    Article  Google Scholar 

  8. Lee S, Kim SB (2019) Parallel Simulated Annealing with a Greedy Algorithm for Bayesian Network Structure Learning. IEEE Trans Knowl Data Eng 32(6):1157–1166

    Article  Google Scholar 

  9. Dempster AP, Laird NM, Rubin DB (1977) Maximum likelihood from incomplete data via the EM algorithm. J R Stat Soc Ser B Stat Methodol 39(1):1–22

  10. Huang L, Cai G, Yuan H, Chen J (2019) A hybrid approach for identifying the structure of a Bayesian network model. Expert Syst Appl 131:308–320

    Article  Google Scholar 

  11. Tsamardinos I, Aliferis CF, Statnikov A (2003) Time and sample efficient discovery of Markov blankets and direct causal relations. In: Proceedings of the Ninth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, pp 673–678

  12. Behjati S, Beigy H (2020) Improved K2 algorithm for Bayesian network structure learning. Eng Appl Artif Intell 91:103617

    Article  Google Scholar 

  13. Jiang Y, Liang Z, Gao H, Guo Y, Zhong Z, Yang C, Liu J (2018) An improved constraint-based Bayesian network learning method using Gaussian kernel probability density estimator. Expert Syst Appl 113:544–554

    Article  Google Scholar 

  14. Pearl J (2014) Probabilistic reasoning in intelligent systems: networks of plausible inference. Elsevier, Amsterdam

  15. Spirtes P, Glymour C (1991) An algorithm for fast recovery of sparse causal graphs. Soc Sci Comput Rev 9(1):62–72

    Article  Google Scholar 

  16. Tsamardinos I, Aliferis CF, Statnikov AR, Statnikov E (2003) Algorithms for large scale Markov blanket discovery. In: Proceedings of the Sixteenth International Florida Artificial Intelligence Research Society Conference, vol 2, pp 376–380

  17. De Morais SR, Aussem A (2010) An efficient and scalable algorithm for local Bayesian network structure discovery. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases, pp 164–179

  18. Suzuki J, Kawahara J (2017) Branch and bound for regular Bayesian network structure learning. In: Conference on Uncertainty in Artificial Intelligence, Sydney, Australia Google Scholar, pp 581–592

  19. Jaakkola T, Sontag D, Globerson A, Meila M (2010) Learning Bayesian network structure using LP relaxations. In: Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, pp 358–365

  20. Bartlett M, Cussens J (2017) Integer linear programming for the Bayesian network structure learning problem. Artif Intell 244:258–271

    Article  MathSciNet  MATH  Google Scholar 

  21. Campos CPd, Ji Q (2011) Efficient structure learning of Bayesian networks using constraints. J Mach Learn Res 12(Mar):663–689

    MathSciNet  MATH  Google Scholar 

  22. Koivisto M, Sood K (2004) Exact Bayesian structure discovery in Bayesian networks. J Mach Learn Res 5(May):549–573

    MathSciNet  MATH  Google Scholar 

  23. Silander T, Myllymaki P (2012) A simple approach for finding the globally optimal Bayesian network structure. arXiv preprint arXiv:1206.6875

  24. Yuan C, Malone BM (2012) An improved admissible heuristic for learning optimal Bayesian networks. In: Proceedings of the Twenty-Eighth Conference on Uncertainty in Artificial Intelligence, Catalina Island, CA, USA, August 14-18, 2012, pp 924–933

  25. Cooper GF, Herskovits E (1992) A Bayesian method for the induction of probabilistic networks from data. Mach Learn 9(4):309–347

    Article  MATH  Google Scholar 

  26. Tabar VR, Eskandari F, Salimi S, Zareifard H (2018) Finding a set of candidate parents using dependency criterion for the K2 algorithm. Pattern Recognit Lett 111:23–29

    Article  Google Scholar 

  27. Ai X (2017) Node importance ranking of complex networks with entropy variation. Entropy 19(7):303

    Article  Google Scholar 

  28. Dash D, Druzdzel MJ (1999) A hybrid anytime algorithm for the construction of causal models from sparse data. In: Proceedings of the Fifteenth International Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann, pp 142–149

  29. Gámez JA, Mateo JL, Puerta JM (2011) Learning Bayesian networks by hill climbing: efficient methods based on progressive restriction of the neighborhood. Data Min Knowl Discov 22(1):106–148

    Article  MathSciNet  MATH  Google Scholar 

  30. Tsamardinos I, Brown LE, Aliferis CF (2006) The max-min hill-climbing Bayesian network structure learning algorithm. Mach Learn 65(1):31–78

    Article  MATH  Google Scholar 

  31. De Campos LM, Castellano JG (2007) Bayesian network learning algorithms using structural restrictions. Int J Approx Reason 45(2):233–254

    Article  MathSciNet  MATH  Google Scholar 

  32. Amirkhani H, Rahmati M, Lucas PJ, Hommersom A (2016) Exploiting experts’ knowledge for structure learning of bayesian networks. IEEE Trans Pattern Anal Mach Intell 39(11):2154–2170

    Article  Google Scholar 

  33. Tang C, Yi Y, Yang Z, Sun J (2016) Risk analysis of emergent water pollution accidents based on a Bayesian Network. J Environ Manage 165:199–205

    Article  Google Scholar 

  34. Wang J, Liu S (2018) Novel binary encoding water cycle algorithm for solving Bayesian network structures learning problem. Knowl Based Syst 150:95–110

    Article  Google Scholar 

  35. Wang J, Liu S (2019) A novel discrete particle swarm optimization algorithm for solving bayesian network structures learning problem. Int J Comput Math 96(12):2423–2440

    Article  MATH  Google Scholar 

  36. Gheisari S, Meybodi MR (2016) Bnc-pso: structure learning of bayesian networks by particle swarm optimization. Inf Sci 348:272–289

    Article  MathSciNet  MATH  Google Scholar 

  37. Chickering DM, Heckerman D, Meek C (2004) Large-sample learning of Bayesian networks is NP-hard. J Mach Learn Res 5(Oct):1287–1330

    MathSciNet  MATH  Google Scholar 

  38. Constantinou AC, Fenton N, Neil M (2016) Integrating expert knowledge with data in Bayesian networks: Preserving data-driven expectations when the expert variables remain unobserved. Expert Syst Appl 56:197–208

    Article  Google Scholar 

  39. Benmohamed E, Ltifi H, Ben Ayed M (2020) Hybrid data analysis approach based on improved K2PC algorithm and expert knowledge: application for assessing impact of the phosphate laundry effluents. In: Proceeding of International Conference on Document Analysis and Recognition ICDAR

  40. Masmoudi K, Abid L, Masmoudi A (2019) Credit risk modeling using Bayesian network with a latent variable. Expert Syst Appl 127:157–166

    Article  Google Scholar 

  41. Benmohamed E, Ltifi H, Ayed MB (2020) Hybrid structure learning approach for assessing the phosphate laundries impact. Int J Comput Inf Eng 14(11):430–436

    Google Scholar 

  42. Benmohamed E, Ltifi H, Ayed MB (2020) A Novel Bayesian Network Structure Learning Algorithm: Best ParentsChildren. In: 2019 IEEE 14th International Conference on Intelligent Systems and Knowledge Engineering (ISKE). IEEE, pp 743-749

  43. Benmohamed E, Ltifi H, Ayed MB (2020) ITNO-K2PC: An improved K2 algorithm with information-theorycentered node ordering for structure learning. Journal of King Saud University-Computer and Information Sciences 2020

  44. Ltifi H, Benmohamed E, Kolski C, Ayed MB (2020) Adapted visual analytics process for intelligent decision-making: application in a medical context. Int J Inf Technol Decis Mak (IJITDM) 19(01):241–282

    Article  Google Scholar 

  45. Ltifi H, Benmohamed E, Kolski C, Ayed MB (2016) Enhanced visual data mining process for dynamic decision-making. Knowl Based Syst 112:166–181

    Article  Google Scholar 

  46. Pineo D, Ware C (2012) Data visualization optimization via computational modeling of perception. IEEE Trans Vis Comput Graph 18(2):309–320

    Article  Google Scholar 

  47. Zheng J, Jiang Z, Chellappa R (2016) Cross-view action recognition via transferable dictionary learning. IEEE Trans Image Process 25(6):2542–2556

    Article  MathSciNet  MATH  Google Scholar 

  48. Chen YC, Wheeler TA, Kochenderfer MJ (2017) Learning discrete Bayesian networks from continuous data. J Artif Intell Res 59:103–132

    Article  MathSciNet  MATH  Google Scholar 

  49. Saraiya P, North C, Duca K (2005) An insight-based methodology for evaluating bioinformatics visualizations, IEEE transactions on visualization and computer graphics, vol 11, pp 443–4564

  50. Khan U, Haleem A (2015) Improving to amart organization: An integrated ISM and fuzzy-MICMAC modelling of barriers. J Manuf Technol Manag 26(6):807–829

    Article  Google Scholar 

Download references

Acknowledgements

The research leading to these results has received funding from the Ministry of Higher Education and Scientific Research of Tunisia under the grant agreement number LR11ES48.

Author information

Authors and Affiliations

  1. REsearch Groups in Intelligent Machines, University of Sfax, National School of Engineers (ENIS), BP 1173, Sfax, 3038, Tunisia

    Emna Benmohamed, Hela Ltifi & Mounir Ben Ayed

  2. Computer Science and Mathematics Department, Faculty of Sciences and Techniques of Sidi Bouzid, University of Kairouan, Kairouan, Tunisia

    Hela Ltifi

  3. Computer Science and Communication Department, Faculty of Sciences of Sfax, Route Sokra Km 3.5- BP, 1171- 3000, Sfax, Tunisia

    Mounir Ben Ayed

Authors
  1. Emna Benmohamed
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hela Ltifi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mounir Ben Ayed
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Emna Benmohamed.

Additional information

Publisher’s Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

(Fig. 15)

Fig. 15
figure 15

Location of the study area in the simplified geologic map [4]

Full size image

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Benmohamed, E., Ltifi, H. & Ayed, M.B. Bayesian model construction based on data-experts oriented approaches for assessing the phosphate effluents effects. Appl Intell 52, 16475–16496 (2022). https://doi.org/10.1007/s10489-021-03105-8

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10489-021-03105-8

Keywords

Search

Navigation