Optimizing pricing and ordering strategies for new products in the presence of consumers with pre-purchase beliefs

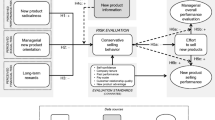
Abstract

The new retail era has dramatically altered consumer behavior, with more people now making purchases based on their pre-purchase beliefs about products, even if they lack prior experience with them. Pre-purchase beliefs represent the anticipated value consumers associate with buying a product or service. This study examines how such beliefs influence consumer purchasing decisions and, in turn, affect retailers’ operational decisions and selling strategies. To achieve this, we create an analytical model that characterizes the consumer decision-making process driven by pre-purchase beliefs and has framed the problem of launching new products as a newsvendor problem. We determine the optimal pricing and ordering strategies for retailers and explored the most effective strategies for different consumer types. Our research indicates that deliberately emphasizing or downplaying product attributes can be more effective in pre-launch marketing than providing strictly accurate information. For value-for-money brands, it’s advisable to adjust the operational strategy to “sell less but at a slightly higher price” as the new product struggles to meet consumer expectations. In markets with diverse consumer segments, retailers must accurately estimate the market sizes of each consumer type and anticipate their pre-purchase beliefs. The value consumers place on these beliefs, along with the market sizes of different consumer categories, play a pivotal role in strategy selection. In summary, this study offers valuable insights into the relationship between consumer purchasing behavior driven by pre-purchase beliefs and retailers’ operational decisions and selling strategy choices.

Appendices

Numerical investigation

In this section, we numerically discuss how reservation utility affects the region of each optimal strategy and how much profit loss can be if retailers ignore or overlook consumers’ pre-purchase beliefs. We set the parameters as follows: $c=3$, $v_0\in [3, 3.8]$, $\beta =0.6$, $N\sim N(120,40^2)$ and $V\sim N(4,2.5^2)$.

1.1 The effect of reservation utility

We start with the effect of reservation utility by varying reservation utility $r_b \in \{1.4,1.6,1.8\}$. Note that $p_S=8$ and $p_0 \in \{3.71,3.43,3.15\}$ under this setting. Figure 7 presents the critical market shares of BS consumers with varying reservation utility. It is clear that a higher reservation utility reduces the size of the area where selling to S and BS is optimal. Since a bigger price discount has to be offered to BS consumers if the reservation utility increases, selling to S and BS is less likely to be optimal.

Fig. 7

Optimal strategy with varying reservation utility

1.2 The consequences of ignoring consumers’ pre-purchase beliefs

Next, we investigated the potential profit loss that retailers could face if they ignore or overlook consumers’ pre-purchase beliefs. We choose the baseline strategy of “selling to S only” as the benchmark. To examine the profit loss from ignoring consumers’ pre-purchase beliefs, we compare the retailer’s profit under the optimal strategy with the profit under the “selling to S only” strategy, i.e., $\max \{\Pi _S,\Pi _A,\Pi _{S+BS}\}$ vs. $\Pi _{S}$. Note that the percentage profit loss from ignoring consumers’ pre-purchase beliefs is measured by $\Delta _{\text {Loss}}:=\frac{\Pi _{S}-\max \{\Pi _S,\Pi _A,\Pi _{S+BS}\}}{\Pi _{S}}\times 100\%$. Figure 8 presents the percentage loss from ignoring consumers’ pre-purchase beliefs when $r_b=1.4$.

Fig. 8

Profit loss from ignoring pre-purchase belief $\Delta _{\text {Loss}}$

Not surprisingly, ignoring consumers’ pre-purchase beliefs does not bring losses only if “selling to S only” is optimal, i.e., most consumers are purely surplus-driven. However, if pre-belief consumers account for a large proportion of the market, then continuing to use the “selling to S only” strategy will result in a considerable profit loss of up to more than 70%. Moreover, ignoring consumers’ pre-purchase beliefs can further exacerbate profit loss if consumers buying decisions are driven by both pre-purchase belief and surplus. For example, when the proportion of surplus-driven consumers is relatively high [low], i.e., $\alpha _S$=70% [30%], then the maximum profit loss is increased from 7.9% (selling to S and BS ) to 31.2% (selling to all) [from 72% to 206%]. This is because the reservation utility demanded by BS consumers further reduces the retailer’s profit.

Lemma and proofs

Lemma 1

If the mean pre-belief demand $\mu _D(v_0)$ has an IBE and the market size distribution $F_N(\cdot )$ has an IGFR, then the expected profit $\Pi (Q^*, p^*)$ is quasi-concave in $v_0$, and there exists a unique consumer pre-purchase belief $v_0^*$ that maximizes the expected profit.

Proof

The first and second derivation of $\Pi (Q^*,p^*)$ with respect to $v_0$ are

$$\begin{aligned} \frac{\partial \Pi (Q^*,p^*)}{\partial v_0}= & {} -v_0f_v(v_0)\int _0^{F_N^{-1}(\frac{v_0-c}{v_0})}xdF_N(x) +\bar{F}_v(v_0)[\frac{c}{v_0}F_N^{-1}(\frac{v_0-c}{v_0})\nonumber \\{} & {} -\int _0^{F_N^{-1}(\frac{v_0-c}{v_0})}F_N(x)dx],\end{aligned}$$

(B.1)

$$\begin{aligned} \frac{\partial ^2\Pi (Q^*,p^*)}{\partial v_0^2}= & {} -v_0f_v'(v_0)\int _0^{F_N^{-1} (\frac{v_0-c}{v_0})}xdF_N(x)-2f_v(v_0)[\frac{c}{v_0}F_N^{-1}(\frac{v_0-c}{v_0})\nonumber \\{} & {} +\int _0^{F_N^{-1}(\frac{v_0-c}{v_0})}F_N(x)dx] +\frac{c^2\bar{F}_v(v_0)}{v_0^3f_N(F_N^{-1}(\frac{v_0-c}{v_0}))}. \end{aligned}$$

(B.2)

Note that $\left. \frac{\partial \Pi (Q^*,p^*)}{\partial v_0}\right| _{v_0=c}=0$ and $\left. \frac{\partial \Pi (Q^*,p^*)}{\partial v_0}\right| _{v_0=\bar{v}}=\bar{v}[\bar{F}_v(\bar{v})]'\int _0^{F_N^{-1}(\frac{\bar{v}-c}{\bar{v}})}xdF_N(x)<0$. Further, $\frac{\partial ^2\Pi (Q^*,p^*)}{\partial v_0^2}\Big |_{v_0=c}=\frac{1}{cf_N(0)}>0$ indicates that there exists at least one solution $v_0^*\in (c,\overline{v}_0)$ such that $\frac{\partial \Pi (Q^*,p^*)}{\partial v_0}\Big |_{v=v_0^*}=0$. For the uniqueness of $v_0^*$, we prove $\left. \frac{\partial ^2\Pi (Q^*,p^*)}{\partial v_0^2}\right| _{v_0=v_0^*}<0$ in the following.

Since we assume that $\mu _D(v_0)$ is IBE, then we have that $\bar{F}_v(v_0)$ is IBE, and

$$\begin{aligned} \frac{de}{dv_0}= & {} -\frac{[v_0[\bar{F}_v(v_0)]''+[\bar{F}_v(v_0)]']\bar{F}_v(v_0)-v_0(\bar{F}_v'(v_0))^2}{\bar{F}_v^2(v_0)}\ge 0, \end{aligned}$$

which we can rewrite as

$$\begin{aligned}{}[-f_v(v_0)]'\le & {} \left( \frac{v_0f_v(v_0)}{\bar{F}_v(v_0)}+1\right) \frac{f_v(v_0)}{v_0}. \end{aligned}$$

(B.3)

Then,

$$\begin{aligned} \frac{\partial ^2\Pi (Q^*,p^*)}{\partial v_0^2}\bigg |_{v=v_0^*}\le & {} -f_v(v_0^*)\big [(\frac{-v_0^*f_v(v_0^*)}{\bar{F}_v(v_0^*)}+1)\int _0^{F_N^{-1} (\frac{v_0^*-c}{v_0^*})}xdF_N(x)\\{} & {} +\frac{2c}{v_0^*}F_N^{-1}(\frac{v_0^*-c}{v_0^*})\big ]\\{} & {} +\frac{c^2\bar{F}_v(v_0^*)}{{v_0^*}^3f_N(F_N^{-1}(\frac{v_0^*-c}{v_0^*}))} =\frac{c\bar{F}_v(v_0^*)}{{v_0^*}^2\int _0^{F_N^{-1}(\frac{v_0^*-c}{v_0^*})}xdF_N(x)}\cdot A(v_0^*), \end{aligned}$$

where

$$\begin{aligned} A(v_0^*)=-F_N^{-1}(\frac{v_0^*-c}{v_0^*})\left( \int _0^{F_N^{-1} (\frac{v_0^*-c}{v_0^*})}xf_N(x)dx+\frac{c}{v_0^*}F_N^{-1} (\frac{v_0^*-c}{v_0^*})\right) \\ +\frac{c\int _0^{F_N^{-1} (\frac{v_0^*-c}{v_0^*})}xdF_N(x)}{v_0^*f_N(F_N^{-1}(\frac{v_0^*-c}{v_0^*}))}. \end{aligned}$$

To complete the proof, we need to show that $A(v_0^*)\le 0$. Let $t=F_N^{-1}(\frac{v_0^*-c}{v_0^*})$ and $r(t)=\frac{f_N(t)}{1-F_N(t)}$. Then, we can rewrite $A(v_0^*)$ as

$$\begin{aligned} A(t)= & {} -t\left( \int _0^txdF_N(x)+t(1-F_N(t))\right) +\frac{\int _0^txdF_N(x)}{r(t)}. \end{aligned}$$

Note that $A(0)=0$ and N has an IGFR that implies that $-\frac{tr'(t)}{r(t)}\le 1$. Thus,

$$\begin{aligned} A'(t)= & {} -\left( \int _0^txdF_N(x)+t(1-F_N(t))\right) -t\big (1-F_N(t)\big ) +\frac{tf_N(t)r(t)-r'(t)\int _0^txdF_N(x)}{r^2(t)}\\\le & {} -t\big (1-F_N(t)\big )-\int _0^txdF_N(x)+\frac{\int _0^txdF_N(x)}{tr(t)}. \end{aligned}$$

Let $B(t)\triangleq -t\big (1-F_N(t)\big )-\int _0^txdF_N(x)+\frac{\int _0^txdF_N(x)}{tr(t)}$. Then, we have

$$\begin{aligned} \lim _{t \rightarrow 0}B(t)=\lim _{t \rightarrow 0}{\frac{\int _0^txdF_N(x)}{tr(t)}}= & {} \lim _{t \rightarrow 0}{\frac{tf_N(t)}{r(t)+tr'(t)}}=0 \text { and } B'(t)=-\frac{[tr(t)]'\int _0^txdF_N(x)}{\big (tr(t)\big )^2}. \end{aligned}$$

By the definition of IGFR; that is, $[tr(t)]'\ge 0$, $B'(t)\le 0$, which implies that $B(t)\le 0$ holds. Since $A'(t)\le B(t)$ and $A(0)=0$, we have $\frac{\partial ^2\Pi (Q^*,p^*)}{\partial v_0^2}\Big |_{v=v_0^*}\le 0$; that is, $\Pi (Q^*,p^*)$ is quasi-concave in $v_0$. This completes the proof. $\square$

1.1 Proof of Proposition 4.1

Since the highest price that consumers are willing to pay is $v_0$, the retailer’s optimal selling price must satisfy $p^*\le v_0$. Since the market demand $D(v_0)$ is independent of the selling price and the expected profit is increasing in p, the retailer would price the product at $v_0$ and extract all consumer surplus, i.e., $p^*=v_0$. Differentiating $\Pi (Q,p^*)$ with respect to Q gives

$$\begin{aligned} \frac{d\Pi (Q,p^*)}{dQ}=p^*-c-p^*F_N(\frac{Q}{\bar{F}_v(v_0)})\quad \text {and}\quad \frac{d^2\Pi (Q,p^*)}{dQ^2}=-p^*f(\frac{Q}{\bar{F}_v(v_0)})<0. \end{aligned}$$

Clearly, $\Pi (Q,p^*)$ is concave in Q. Then there is a unique $Q^*$ such that $\frac{d\Pi (Q,p^*)}{dQ}|_{Q=Q^*}=0$, that is $Q^*=\bar{F}_v(v_0)F_N^{-1}(\frac{v_0-c}{v_0})$. Accordingly, $\Pi (Q^*,p^*)=v_0\bar{F}_v(v_0)\int _0^{F_N^{-1}(\frac{v_0-c}{v_0})}xdF_N(x)$.

1.2 Proof of Proposition 4.2

We omit the proof details for optimal decisions. Here we only prove the monotonicity of $p_0$. From Equation (4), the first derivation of $p_0$ with respect to $r_b$ is

$$\begin{aligned} \frac{dp_0}{dr_b}=\frac{F_v(p_0+r_b)+2r_bf_v(p_0+r_b)}{-1-2r_bf_v(p_0+r_b)+F_v(p_0+r_b)}. \end{aligned}$$

Since $-(1-F_v(p+r_b))\le 0$ and $F_v(p+r_b)+2r_bf_v(p+r_b)\ge 0$, we have $\frac{dp}{dr_b}\le 0$. Replacing $v_0$ by $p_0$ in Equation (4), we can find a critical $\hat{r}_b$ such that $U_{BS}(p_0(\hat{r}_b))=U_{BS}(v_0)=0$.

1.3 Proof of Proposition 5.1

Overpricing (i.e., $p > v_0$) will prevent pre-belief consumers. However, underpricing (i.e., $p \le v_0$) will attract both types of consumers, but may result in profit loss due to offering too much of a discount for BS consumers. Therefore, we discuss the problem in two cases: $v_0<p$ and $v_0\ge p$. For $v_0< p$, since B consumers never buy in this case, selling to all is identical to selling to BS only. By Proposition 4.2, the optimal decisions and the correspondingly maximal expected profit are $p^*=p_0$, $Q^*=\alpha _{BS}\bar{F}_v(p_0+r_b)F_N^{-1}(\frac{p_0-c}{p_0})$ and $\Pi _{BS}(p^*,Q^*)=\alpha _{BS}K(p_0,r_b)$. For $v_0\ge p$, all consumers with pre-purchase beliefs consider buying. By Proposition 4.1, we have $p^*=v_0$, $Q^*=\bar{F}_v(v_0)F_N^{-1}(\frac{v_0-c}{v_0})$ and $\Pi _{A}(p^*,Q^*)=K(v_0,0)$. The profit difference between the two selling strategies is

$$\begin{aligned} \Delta \Pi= & {} \Pi _{A}-\Pi _{BS}=K(v_0,0)-\alpha _{BS}K(p_0,r_b)\\= & {} v_0\bar{F}_v(v_0)\int _0^{F_N^{-1}(\frac{v_0-c}{v_0})}xdF_N(x) -\alpha _{BS}p_0\bar{F}_v(p_0+r_b)\int _0^{F_N^{-1}(\frac{p_0-c}{p_0})}xdF_N(x). \end{aligned}$$

Taking the first derivation of $\Delta \Pi$ with respect to $\alpha _{BS}$ gives $\frac{d \Delta \Pi }{d\alpha _{BS}}=-K(p_0,r_b)<0$ which indicates that $\Delta \Pi$ is decreasing in $\alpha _{BS}$. Note that $\Delta \Pi |_{\alpha _{BS}=0}=K(v_0,0)>0$. If $\Delta \Pi |_{\alpha _{BS}=1}=K(v_0,0)-K(p_0,r_b)>0$, then $\Delta \Pi \ge 0$ always holds. Otherwise, there exists a critical market share ${{\tilde{\alpha }}}_{BS}$ such that $\Delta \Pi ({{\tilde{\alpha }}}_{BS})=0$. If $\alpha _{BS}\le {{\tilde{\alpha }}}_{BS}$, then $\Delta \Pi \ge 0$; otherwise $\Delta \Pi \le 0$. To complete the proof, we next verify the sign of $\Delta \Pi |_{\alpha _{BS}=1}$.

It follows from Lemma 1 that $K(v_0,0)$ is quasi-concave in $v_0$. This implies that $\Delta \Pi |_{\alpha _{BS}=1}=K(v_0,0)-K(p_0,r_b)$ is quasi-concave in $v_0$. Note that, by Proposition 4.2, selling to BS exists only if $p_0\ge v_0$ for any given $v_0$. Therefore, to ensure both strategies exist, the admissible range of $v_0$ should be $[c,p_0]$. Since $\Delta \Pi |_{\alpha _{BS}=1}(v_0=c)=-K(p_0,r_b)<0$ and $\lim \limits _{v_0\rightarrow p_0}\Delta \Pi |_{\alpha _{BS}=1}(v_0)=K(p_0,0)-K(p_0,r_b)\ge 0$, there exists a unique $\tilde{v_0}$ such that $\Delta \Pi |_{\alpha _{BS}=1}(\tilde{v}_0)=0$. If $v_0\le \tilde{v}_0$, then $\Delta \Pi |_{\alpha _{BS}=1}\le 0$; otherwise, $\Delta \Pi |_{\alpha _{BS}=1}\ge 0$.

1.4 Proof of Proposition 6.1

1.4.1 (a) $p_0\le v_0^L\le v_0^H$

The optimal decisions of high pricing are $p^*=v_0^H$ and $Q^*=\alpha _H\bar{F}_v(v_0^H)F_N^{-1}(\frac{v_0^H-c}{v_0^H})$. For low pricing, we have $p^*=v_0^L$ and $Q^*=[\alpha _H\bar{F}_v(v_0^H)+\alpha _L\bar{F}_v(v_0^L)]F_N^{-1}(\frac{v_0^L-c}{v_0^L})$. Correspondingly, the maximum profits of high and low pricing are $\Pi _{H}=\Pi _{HB}+\Pi _{HBS}=\alpha _HK(v_0^H,0)$ and $\Pi _{A}=\Pi _{HB}+\Pi _{HBS}+\Pi _{LB}+\Pi _{LBS}=\alpha _HK(v_0^L,\Delta _{v_0})+\alpha _LK(v_0^L,0)$, respectively. The profit difference between the two selling strategies is

$$\begin{aligned} \Delta \Pi= & {} \Pi _{A}-\Pi _{H}=\alpha _H(K(v_0^L,\Delta _{v_0})-K(v_0^L,0)-K(v_0^H,0))+K(v_0^L,0). \end{aligned}$$

Since $K(v_0^L,\Delta _{v_0})\le K(v_0^L,0)$, it is clear that $\Delta \Pi$ is decreasing in $\alpha _H$. Note that $\Delta \Pi |_{\alpha _H=0}>0$. So, there must exist a critical $\hat{\alpha }_H^0$ such that $\Delta \Pi (\hat{\alpha }_H^0)=0$. If $\alpha _H\le {\hat{\alpha }}_H^0$, then $\Delta \Pi \ge 0$; otherwise, $\Delta \Pi \le 0$.

1.4.2 (b) $v_0^L\le p_0\le v_0^H$

By comparing the profits of any two strategies, we have the following results.

• (I) (Selling to All vs. Selling to H) See part (a).

• (II) (Selling to All vs. Selling to H and LBS) There exists a critical market share $\hat{\alpha }_H^{1}$ such that $\Pi _{H+LBS}(\hat{\alpha }_H^{1})=\Pi _{A}(\hat{\alpha }_H^{1})$. If $\alpha _H\le \hat{\alpha }_H^{1}$, then $\Pi _{A}\ge \Pi _{H+LBS}$; otherwise, $\Pi _{A}\le \Pi _{H+LBS}$.

• (III) (Selling to H vs. Selling to H and LBS) There exists a critical market share of high-belief consumers $\hat{\alpha }_H^2$ such that $\Pi _{H+LBS}(\hat{\alpha }_H^{2})=\Pi _{H}(\hat{\alpha }_H^{2})$. If $\alpha _H\le \alpha _H^{2}$, then $\Pi _{H+LBS}\ge \Pi _{H}$; otherwise, $\Pi _{H}\ge \Pi _{H+LBS}$.

Note that $K(v_0^H,0)\ge K(p_0,v_0^H-p_0)\ge K(v_0^L, \Delta _{v_0})$ for $v_0^L< p_0\le v_0^H$. So we have

$$\begin{aligned} \frac{d\hat{\alpha }_H^1}{d\alpha _{BS}}= & {} \frac{K(p_0,r_b)(K(v_0^L,\Delta _{v_0}) -K(p_0,v_0^H-p_0))}{[K(p_0,v_0^H-p_0)+K(v_0^L,0)-K(v_0^L,\Delta _{v_0})-\alpha _{BS}K(p_0,r_b)]^2}\le 0,\\ \frac{d\hat{\alpha }_H^2}{d\alpha _{BS}}= & {} \frac{K(p_0,r_b)(K(v_0^H,0)-K(p_0,v_0^H-p_0))}{[K(v_0^H,0)+\alpha _{BS}K(p_0,r_b)-K(p_0,v_0^H-p_0)]^2}\ge 0. \end{aligned}$$

Further, we have $\hat{\alpha }_H^2|_{\alpha _{BS}=0}=0$, $\hat{\alpha }_H^2|_{\alpha _{BS}=1}=\frac{K(p_0,r_b)}{K(p_0,r_b)+K(v_0^H,0)-K(p_0,v_0^H-p_0)}<1$, and

$$\begin{aligned} \hat{\alpha }_H^1|_{\alpha _{BS}=0}= & {} \frac{K(v_0^L,0)}{K(p_0,v_0^H-p_0)+K(v_0^L,0)-K(v_0^L,\Delta _{v_0})}\\\ge & {} \frac{K(v_0^L,0)}{K(v_0^H,0)+K(v_0^L,0)-K(v_0^L,\Delta _{v_0})}=\hat{\alpha }_H^0,\\ \hat{\alpha }_H^1|_{\alpha _{BS}=1}= & {} \frac{K(v_0^L,0)-K(p_0,r_b)}{K(p_0,v_0^H-p_0)-K(v_0^L,\Delta _{v_0})+K(v_0^L,0)-K(p_0,r_b)}<1. \end{aligned}$$

Therefore, $\hat{\alpha }_H^1$ and $\hat{\alpha }_H^2$ intersect with $\hat{\alpha }_H^0$ at $\hat{\alpha }_{BS}^1$ and $\hat{\alpha }_{BS}^2$, respectively. Further, it is easy to verify that $\hat{\alpha }_{BS}^1=\hat{\alpha }_{BS}^2=\frac{K(v_0^L,0)}{K(p_0,r_b)}\cdot \frac{K(p_0,v_0^H-p_0)-K(v_0^H,0)}{K(v_0^L,\Delta _{v_0})-K(v_0^H,0)}$. This implies that three critical market shares have a common intersection. Therefore, selling to all is best if $\alpha _H\le \min \{{\hat{\alpha }}_H^0, {\hat{\alpha }}_H^1\}$; selling to H is best if $\alpha _H\ge \max \{{\hat{\alpha }}_H^0, {\hat{\alpha }}_H^2\}$, otherwise selling to H and LBS is best.

1.4.3 (c) $v_0^L\le v_0^H\le p_0$

By comparing the profits of any two strategies, we have

• (I) (Selling to All vs. Selling to BS) There exists a critical market share of H consumers ${\check{\alpha }}_H^0$ such that $\Pi _{A}({\check{\alpha }}_H^0)=\Pi _{BS}$. If $\alpha _H\le {\check{\alpha }}_H^0$, then selling to all consumers is best; otherwise, selling to BS consumers is best.

• (II) (Selling to All vs. Selling to H and LBS consumer) There exists a critical market share of H consumers ${\check{\alpha }}_H^1$ such that $\Pi _{A}({\check{\alpha }}_H^1)=\Pi _{H+LBS}({\check{\alpha }}_H^1)$. If $\alpha _H\le {\check{\alpha }}_H^1$, then selling to all consumers is best; otherwise, selling to H and LBS is best.

• (III) (Selling to H and LBS vs. Selling to BS) There exists a critical market share of H consumers ${\check{\alpha }}_H^2$ such that $\Pi _{H+LBS}({\check{\alpha }}_H^2)=\Pi _{BS}$. If $\alpha _H\ge {{\check{\alpha }}}_H^2$, then selling to H and LBS is best; otherwise, selling to BS consumers is best.

Note that $K(v_0^H,0)\ge K(v_0^L, \Delta _{v_0})$, $K(v_0^H,0)\ge K(v_0^H, r_b)$ and $K(v_0^L,0)\ge K(v_0^L, \Delta _{v_0})$. If critical market shares exist, then we have $\frac{d\hat{\alpha }_H^0}{d\alpha _{BS}}\le 0$,

$$\begin{aligned} \frac{d{\check{\alpha }}_H^1}{d\alpha _{BS}}= & {} \frac{K(v_0^H,r_b)(K(v_0^L,\Delta _{v_0}) -K(v_0^H,0))}{[K(v_0^H,0)+K(v_0^L,0)-\alpha _{BS}K(v_0^H,r_b)-K(v_0^L,\Delta _{v_0})]^2}\le 0,\\ \frac{d{\check{\alpha }}_H^2}{d\alpha _{BS}}= & {} \frac{K(v_0^H,0)(K(p_0,r_b)-K(v_0^H,r_b))}{[K(v_0^H,0)-\alpha _{BS}K(v_0^H,r_b)]^2}\ge 0. \end{aligned}$$

Note that ${\check{\alpha }}_H^0|_{\alpha _{BS}=0}\ge 1$, ${\check{\alpha }}_H^1|_{\alpha _{BS}=0}\ge 0$ and ${\check{\alpha }}_H^2|_{\alpha _{BS}=0}=0$. Further, it is easy to verify that ${\check{\alpha }}_H^0$, ${\check{\alpha }}_H^1$ and ${\check{\alpha }}_H^2$ intersect at the same point ${\check{\alpha }}_{BS}$, i.e., there is a critical ${\check{\alpha }}_{BS}$ such that ${\check{\alpha }}_H^0({\check{\alpha }}_{BS})={\check{\alpha }}_H^1({\check{\alpha }}_{BS})={\check{\alpha }}_H^2({\check{\alpha }}_{BS})$.

1.5 Proof of Proposition 6.2

By comparing the profits of any two strategies, we have

• (I) (Selling to S vs. Selling to All) The profit difference between selling to S and selling to all is $\Delta \Pi =\Pi _S-\Pi _A=\alpha _SK(p_S,0)-K(v_0,0)$. Clearly, $\Delta \Pi$ is increasing in $\alpha _S$. Note that $\Delta \Pi |_{\alpha _S=0}<0$ and $\Delta \Pi |_{\alpha _S=1}=K(p_S,0)-K(v_0,0)$. If $K(p_S,0)-K(v_0,0)\le 0$, then $\Delta \Pi <0$ always holds; otherwise, there exists a critical market share ${\hat{\alpha }}_S^0$ such that $\Delta \Pi ({\hat{\alpha }}_S^0)=0$. If $\alpha _S\ge {\hat{\alpha }}_S^0$, then selling to S consumers only is best; otherwise, selling to all consumers is best.

• (II) (Selling to S and BS vs. Selling to All) The profit difference between selling to S+BS and selling to all is

  $$\begin{aligned} \Delta \Pi= & {} \Pi _{S+BS}-\Pi _{A}=\alpha _SK(p_0,0)+\beta (1-\alpha _{S})K(p_0,r_b)-K(v_0,0). \end{aligned}$$

  Taking the first derivation of $\Delta \Pi$ with respect to $\alpha _S$ gives that $\frac{d\Delta \Pi }{d\alpha _S}=K(p_0,0)-\beta K(p_0,r_b)>0$ holds for any given $\beta$, which indicates that $\Delta \Pi$ is increasing in $\alpha _S$. Note that $\Delta \Pi |_{\alpha _S=1}=K(p_0,0)-K(v_0,0)$ and $\Delta \Pi |_{\alpha _S=0}=\beta K(p_0,r_b)-K(v_0,0)$. If $(K(p_0,0)-K(v_0,0))(\beta K(p_0,r_b)-K(v_0,0))\ge 0$, then $\Delta \Pi >0$ or $\Delta \Pi <0$ always holds; otherwise, there exists a critical market share ${\hat{\alpha }}_S^1$ such that $\Delta \Pi ({\hat{\alpha }}_S^1)=0$. If $\alpha _S\ge {\hat{\alpha }}_S^1$, then selling to S and BS is best; otherwise selling to all is best.

• (III) (Selling to S only vs. Selling to S and BS) The profit difference between selling to S and selling to S+BS is

  $$\begin{aligned} \Delta \Pi= & {} \Pi _{S}-\Pi _{S+BS}=\alpha _SK(p_S,0)-\alpha _SK(p_0,0)-\beta (1-\alpha _{S})K(p_0,r_b)\\= & {} \alpha _S[K(p_S,0)-K(p_0,0)+\beta K(p_0,r_b)]-\beta K(p_0,r_b). \end{aligned}$$

  Taking the first derivation of $\Delta \Pi$ with respect to $\alpha _S$ gives $\frac{d\Delta \Pi }{d\alpha _S}=K(p_S,0)-K(p_0,0)+\beta K(p_0,r_b)>0$, which indicates that $\Delta \Pi$ is increasing in $\alpha _S$. Note that $\Delta \Pi |_{\alpha _S=1}=K(p_S,0)-K(p_0,0)$ and $\Delta \Pi |_{\alpha _S=0}=-\beta K(p_0,r_b)\le 0$. If $K(p_S,0)-K(p_0,0)\le 0$, then $\Delta \Pi <0$ always holds; otherwise, there exists a critical market share ${\hat{\alpha }}_S^2$ such that $\Delta \Pi ({\hat{\alpha }}_S^2)=0$. If $\alpha _S\ge {\hat{\alpha }}_S^2$, then selling to S only is best; otherwise, selling to S and BS is best.

Note that ${\hat{\alpha }}_S^0|_{v_0=c}=0$, ${\hat{\alpha }}_S^1|_{v_0=c}<0$, and ${\hat{\alpha }}_S^i$ exists only if $K(p_s,0)\ge K(p_0,0)\ge K(v_0,0)$ where $i\in \{1, 2,3\}$ and $v_0\le p_0\le p_S$. By Lemma 1, we have ${\hat{\alpha }}_S^0$ and ${\hat{\alpha }}_S^1$ are quasi-concave in $v_0$ and ${\hat{\alpha }}_S^2$ is independent with $v_0$. Then, it is easy to verify that there is a critical $\hat{v}_0$ such that ${\hat{\alpha }}_S^0(\hat{v}_0)={\hat{\alpha }}_S^1(\hat{v}_0)={\hat{\alpha }}_S^2$, i.e., $\hat{v}_0$ satisfies $K(\hat{v}_0,0)=\frac{\beta K(p_S,0)K(p_0,r_b)}{K(p_S,0)-K(p_0,0)+\beta K(p_0,r_b)}$. Therefore, selling to all is best if $\alpha _S\le {\hat{\alpha }}_S^0$ for $v_0\ge \hat{v}_0$ or $\alpha _S\le {\hat{\alpha }}_S^1$ for $v_0\le \hat{v}_0$; selling to S is best if ${\hat{\alpha }}_S^1\le \alpha _S\le {\hat{\alpha }}_S^2$; otherwise, selling to S and BS is best.