Abstract
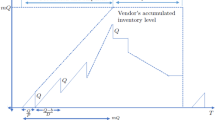
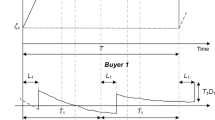
This paper develops a continuous-review vendor-buyer supply chain (SC) model wherein the lead-time (taken as replenished) is considered as a factor affected upon by the time stamp required for setup and production followed by transportation. Here, the production time indicates the interaction between the lot-size and lead-time. Assuming the existence of an opportunity with the buyer of reducing the replenishment lead-time. The buyer receives normally distributed stochastic lead-time demands from its customers. Due to the stochastic nature of lead-time demand, shortages may arise at the buyer’s side which is fully backlogged. We presume imperfection production at the vendor’s end, which leads to the generation of a certain ratio/percentage of defective products, which results in additional warranty costs for the vendor. This study intends to uncover the best policy that minimizes the system’s total expected cost. A solution algorithm with some lemmas is provided which helped in finding the optimal solution and to prove the uniqueness of the solutions. Findings demonstrate that a reduction in lead-time can effectively lower safety stock as well as the total cost.



















Similar content being viewed by others
References
Aljazzara, S. M., Jaber, M. Y., & Moussawi-Haidar, L. (2017). Coordination of a three-level supply chain (supplier-manufacturer-retailer) with permissible delay in payments and price discounts. Applied Mathematical Modelling, 48, 289–302.
Banerjee, A. (1986). A joint economic-lot-size model for purchaser and vendor. Decision Sciences, 17, 292–311.
Ben-Daya, M., & Hariga, M. (2004). Integrated single vendor single buyer model with stochastic demand and variable lead-time. International Journal of Production Economics, 92, 75–80.
Ben-Daya, M., & Raouf, A. (1994). Inventory models involving lead-time as a decision variable. The Journal of the Operations Research Society, 45, 579–582.
Braglia, M., Castellano, D., & Frosolini, M. (2015). A novel approach to safety stock management in a coordinated supply chain with controllable lead-time using present value. Applied Stochastic Models in Business and Industry. https://doi.org/10.1002/asmb.2126.
Buratto, A., Cesaretto, R., & Giovanni, P. D. (2019). Consignment contracts with cooperative programs and price discount mechanisms in a dynamic supply chain. International Journal of Production Economics, 218, 72–82.
Cavalcante, C., & do Nascimento, T. G., & Lopes, R. S. (2016). Multi-attribute Utility Theory analysis for burn-in processes combined with replacement. Eksploatacja i Niezawodnosc-Maintenance and Reliability, 18, 599–605.
David, I., & Eben-Chaime, M. (2008). How accurate is the integrated vendor continuous model? International Journal of Production Economics, 114, 805–810.
Dey, O., & Giri, B. C. (2019). A new approach to deal with learning in inspection in an integrated vendor-buyer model with imperfect production process. Computers & Industrial Engineering, 131, 515–523.
Eben-Chaime, M. (2004). The effect of discreteness in vendor-buyer relationships. IIE Transactions, 36, 583–589.
Ertogral, K., Darwish, M., & Ben-Daya, M. (2007). Production and shipment lot sizing in a vendor supply chain with transportation cost. European Journal of Operational Research, 176, 1592–1606.
Glock, C. H. (2012). Lead-time reduction strategies in a single-vendor-single-buyer integrated inventory model with lot size-dependent lead-times and stochastic demand. International Journal of Production Economics, 136, 37–44.
Glock, C. H., & Ries, J. M. (2013). Reducing lead-time risk through multiple sourcing: the case of stochastic demand and variable lead-time. International Journal of Production Research, 51, 43–56.
Govindan, K. (2015). The optimal replenishment policy for time-varying stochastic demand under vendor managed inventory. European Journal of Operational Research, 242, 402–423.
Goyal, S. K. (1976). An integrated inventory model for a single supplier-single customer problem. International Journal of Production Research, 15, 107–111.
Hadley, G., & Whitin, T. (1963). Analysis of inventory systems. Prentice-Hall.
Hariga, M. A. (1999). A stochastic inventory model with lead-time and lot size interaction. Production Planning & Control, 10, 434–438.
Heydari, J., Zaabi-Ahmadi, P., & Choi, T. M. (2018). Coordinating supply chains with stochastic demand by crashing lead-times. Computers & Operations Research, 100, 394–403.
Hossain, S. J., Ohaiba, M., & Sarker, B. R. (2017). An optimal vendor-buyer cooperative policy under generalized lead-time distribution with penalty cost for delivery lateness. International Journal of Production Economics, 188, 50–62.
Hsiao, Y. C. (2008). A note on integrated single vendor single buyer model with stochastic demand and variable lead-time. International Journal of Production Economics, 114, 294–297.
Hsiao, Y. C. (2008). Integrated logistic and inventory model for a two-stage supply chain controlled by the reorder and shipping points with sharing information. International Journal of Production Economics, 115, 229–235.
Hsu, S. L., & Huang, Y. F. (2009). An integrated inventory model with controllable lead-time and distribution-free demand. Applied Stochastic Models in Business and Industry, 26, 416–430.
Huang, C. K. (2004). An optimal policy for a single-vendor single-buyer integrated production-inventory problem with process unreliability consideration. International Journal of Production Economics, 91, 91–98.
Jha, J. K., & Shanker, K. (2013). Single-vendor multi-buyer integrated production-inventory model with controllable lead-time and service level constraints. Applied Mathematical Modelling, 37, 1753–1767.
Juran, J. M., & Gryna, F. M. (2016). The quality control handbook (7th ed., p. 2016). McGraw- Hill.
Kazemi, N., Abdul-Rashid, S. H., Ghazilla, R. A. R., Shekarian, E., & Zanoni, S. (2018). Economic order quantity models for items with imperfect quality and emission considerations. International Journal of System Science: Operations & Logistic, 5, 99–115.
Kim, J. S., & Benton, W. C. (1995). Lot size dependent lead-times in a Q, R inventory system. International Journal of Production Economics, 33, 41–58.
Kim, S. J., Sarkar, B., & Sarkar, S. (2018). An inventory model with backorder price discount and stochastic lead-time. DJ Journal of Engineering and Applied Mathematics, 42(2018), 34–48.
Krikke, H., Blanc, L., & Van de Velde, S. (2004). Product modularity and the design of closed-loop supply chains. California Management Review, 46, 23–39.
Li, Y., Xu, X., & Ye, F. (2011). Supply chain coordination model with controllable lead-time and service level constraint. Computers & Industrial Engineering, 61, 858–864.
Liao, C. J., & Shyu, C. H. (1991). An analytical determination of lead-time with normal demand. International Journal of Operations & Production Management, 11, 72–78.
Lin, H. J. (2016). Investing in lead-time variability reduction in a collaborative vendor-buyer supply chain model with stochastic lead-time. Computers & Operations Research, 72, 43–49.
Mou, Q., Cheng, Y., & Liao, H. (2017). A note on lead-time reduction strategies in a single-vendor-single-buyer integrated inventory model with lot size-dependent lead-times and stochastic demand. International Journal of Production Economics, 193, 827–831.
Moon, I. K., & Cha, B. C. (2005). A continuous review inventory model with the controllable production rate of the manufacturer. International Transactions in Operational Research, 12(2), 247–258.
Ouyang, L. Y., Yeh, N. C., & Wu, K. S. (1996). Mixture inventory model with backorders and lost sales for variable lead-time. Journal of the Operations Research Society, 47, 829–832.
Ouyang, L. Y., Wu, K. S., & Ho, C. H. (2004). Integrated vendor-buyer cooperative models with stochastic demand in controllable lead-time. International Journal of Production Economics, 92, 255–266.
Ouyang, L. Y., Wu, K. S., & Ho, C. H. (2007). An integrated vendor-buyer inventory model with quality improvement and lead-time reduction. International Journal of Production Economics, 108, 349–358.
Pan, J. C., & Yang, J. S. (2002). A study of an integrated inventory with controllable lead-time. International Journal of Production Economics, 40, 1263–1273.
Ponte, B., Costas, J., Puche, J., Pino, R., & Fuente, D. (2018). The value of lead-time reduction and stabilization: A comparison between traditional and collaborative supply chains. Transportation Research Part E: Logistics and Transportation Review, 111, 165–185.
Priyan, S., & Uthayakumar, R. (2014). Trade credit financing in the vendor buyer inventory system with ordering cost reduction, transportation cost and backorder price discount when the received quantity is uncertain. Journal of Manufacturing System, 33, 654–674.
Rad, R. H., Razmi, J., Sangari, M. S., & Ebrahimi, Z. F. (2014). Optimizing an integrated vendor-managed inventory system for a single-vendor two-buyer supply chain with determining weighting factor for vendor’s ordering cost. International Journal of Production Economics, 153, 295–308.
Ryu, S. W., & Lee, K. K. (2003). A stochastic inventory model of dual sourced supply chain with lead-time reduction. International Journal of Production Economics, 81–82, 513–524.
Sarkar, S., Giri, B. C., & Sarkar, A. K. (2019). A vendor-buyer inventory model with lot-size and production rate dependent lead-time under time value of money. RAIRO-Operations Research, 54, 961–979.
Sainathan, A., & Groenevelt, H. (2018). Vendor managed inventory contracts-coordinating the supply chain while looking from the vendor’s perspective. European Journal of Operational Research, 272, 249–260.
Sarkar, S., & Giri, B. C. (2020). Stochastic supply chain model with imperfect production and controllable defective rate. International Journal of System Science: Operations & Logistics, 2(2020), 133–146.
Sarkar, B., Mandal, B., & Sarkar, S. (2015). Quality improvement and backorder price discount under controllable lead-time in an inventory model. Journal of Manufacturing System, 35, 26–36.
Taleizadeh, A. A., Shokr, I., & Joali, F. (2020). Optimizing vendor-managed inventory systems with limited storage capacity and partial backordering under stochastic demand. RAIRO-Operations Research, 54, 179–209.
Tersine, R. J. (2002). Principles of inventory and materials management, fourthed. Prentice Hall.
Tiwari, S., Kazemi, N., Modak, N. M., Cárdenas-Barrón, L. E., & Sarkar, S. (2020). The effect of human errors on an integrated stochastic supply chain model with setup cost reduction and backorder price discount. International Journal of Production Economics, 226, 107643.
Tiwari, S., Daryanto, Y., & Wee, H. M. (2018). Sustainable inventory management with deteriorating and imperfect quality items considering carbon emission. Journal of Cleaner Production, 192, 281–292.
Tiwari, S., Sana, S. S., & Sarkar, S. (2018). Joint economic lot sizing model with stochastic demand and controllable lead-time by reducing ordering cost and setup cost. Revista de la Real Academia de Ciencias Exactas Físicas y Naturales. Serie A. Matemáticas, 112, 1075–1099.
Yang, J. S., & Pan, J. C. (2004). Just-in-time purchasing: An integrated inventory model involving deterministic variable lead-time and quality improvement investment. International Journal of Production Research, 42, 853–863.
Yang, J. Q., Zhang, X. M., Fu, H. Y., & Liu, C. (2017). Inventory competition in a dual-channel supply chain with delivery lead-time consideration. Applied Mathematical Modelling, 42, 675–692.
Acknowledgements
We thank the editor-in-chief and anonymous reviewers for their constructive comments. The work of first author is supported by JU-RUSA 2.0 Doctoral Scholarship, Jadavpur University, Kolkata, India under Ref. No. R-11/197/2019. The second author author would like to express his gratitude to NRF Singapore (Grant NRF-RSS2016-004) for financial assistance to carry out this research work.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Proof of Lemma 1
Proof
We have the second order derivative derivative of \(\Pi _{sc}\) as
where \(E_{1}=\frac{\sigma k_{1}h_{B}}{2P}>0,\)
\(E_{2}=\frac{\sigma \pi D\Psi (k_{1})}{2mP(1-E[Y])}>0,\)
\(E_{3}=\frac{D}{1-E[Y]}\left\{ F+\frac{S_{B}+S_{V}}{m}+\left( 1-\frac{1}{m}\right) \pi \sigma \sqrt{\kappa _{t0}e^{-aW}}\Psi (k_{2})\right\} >0,\)
\(E_{4}=\frac{D\sigma \pi }{m(1-E[Y])}\left( \kappa _{t0}e^{-aW}+s_{t}\right) \Psi (k_{1})>0,\)
\(E_{5}=\frac{(m-1)\sigma \pi Dk_{1}[1-\Phi (k_{2})]}{2mP(1-E[Y])}>0.\)
As the first and second terms of (25) within the bracket converge to zero for large Q, and therefore it is obvious that \(\frac{\partial ^2 \Pi _{sc}}{\partial Q^2}<0\) for large value of Q, and hence clearly \(\left| \frac{\partial ^2 \Pi _{sc}}{\partial Q^2}\right| _{Q=\infty }=0.\) Therefore, \(\Pi _{sc}(Q,k_{1},W,m)\) is not convex in Q.
To prove the existence of the unique solution, we consider the following.
The first-order partial derivative of \(\Pi _{sc}(Q,k_{1},W,m)\) with respect to Q for given \(k_{1}, W,\) and m is given by
which can be rewritten as
where \(H(m)=\frac{h_{V}}{2}\left( m-1-\frac{D(m-2)}{P(1-E[Y])}\right) +\frac{h_{B}}{1-E[Y]}\left( \frac{E[(1-Y)^2]}{2}+\frac{DE[Y]}{x}\right) >0.\)
In (26), the last four terms within the bracket converge to zero for large Q and it is certain that \(\left| \frac{\partial \Pi }{\partial Q}\right| _{Q=\infty }=H(m)>0.\)
then \(\frac{\partial \Pi }{\partial Q}\ge 0\) for all Q which implies that \(\Pi _{sc}\) is a strictly increasing function of Q and the optimal solution is the possible minimum lot size \(Q_{min}\).
then it is clear that the sign of the first-order partial derivative changes from negative to positive only once for \(1\le Q<\infty .\) This means that \(\frac{\partial \Pi _{sc}}{\partial Q}=0\) has a unique solution for fixed \(k_{1},W,\) and m. The sign of the first-order derivative indicates that \(\Pi _{sc}\) gradually increases after a point of inflection. Thus, for fixed \(k_{1},W,\) and m, there exists an optimal solution that can be determined uniquely in Q.
Hence, Lemma 1 is proved. \(\square \)
Appendix B: Proof of Lemma 2
Proof
Now, evaluating first and second order partial derivatives of \( \Pi _{sc}\) w.r.t. \(k_{1}\):
and
Since \(\frac{\partial ^2 \Pi _{sc}}{\partial k_{1}^2}>0\), we can conclude that the cost function \(\Pi _{sc}\) is convex w.r.t. \(k_{1}.\) Hence, Lemma 2 is proved. \(\square \)
Rights and permissions
About this article
Cite this article
Sarkar, S., Tiwari, S. & Giri, B.C. Impact of uncertain demand and lead-time reduction on two-echelon supply chain. Ann Oper Res 315, 2027–2055 (2022). https://doi.org/10.1007/s10479-021-04105-0
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-021-04105-0