Combined effects of ENSO and PDO on activity of major hurricanes in the eastern North Pacific

Abstract

Major hurricanes (MHs) in the eastern North Pacific (ENP) in 1970–2020 are clustered into 3 categories with different quantity, intensity, lifetime, and track. MHs in all three clusters are more active in the Pacific Decadal Oscillation (PDO) warm than cold phases. However, only the relationship between MHs in the western part of ENP (cluster A) and El Niño Southern Oscillation (ENSO) is significantly modulated by the PDO. This cluster is more active during El Niño than La Niña years in the PDO cold phases, which results from the local sea surface temperature (SST) warm anomalies caused by the combined influences of ENSO and the PDO. Warmer SST can make a stronger ascending flow, and strengthen the local activity of MHs by leading to anomalous atmospheric circulation. In the PDO warm phases, however, there is no distinct local SST anomalies between two ENSO phases. Therefore, the modulation of PDO on ENSO and cluster A only occurs in the PDO negative phases. In the region of the eastern part of ENP where two other clusters are located, the PDO hardly modulates the relationship between ENSO and MHs activity as the PDO exerts little influences on the ENSO-related SST patterns in both the positive and negative phases. The conclusion is also supported by first mode of empirical orthogonal functions analysis for interannual MHs activity. Therefore, the PDO modulation cannot be ignored when predicting the activity of tropical cyclones in the ENP, especially for MHs with strong wind and rainstorm.

APPENDIX

1.1 Clustering method and the number of clusters

The clustering method mainly applies a finite mixture model (e.g., Everitt and Hand 1981) which uses a convex linear combination of component density functions to represent the MH tracks data distribution. Then we use a set of basic component densities to model highly non-Gaussian or multimodal densities. In order to extend the standard regression mixture modeling framework, we replace the marginal component densities with conditional density components in the regression mixture models. The new conditional densities are functions of the MH’s positions, and the MH positions are conditioned on an independent variable (i.e., time). Through quadratic polynomial regression functions, the component densities can model the MH’s longitudes and latitudes versus time. The quadratic polynomial regression functions are used to fit the geographical ‘shape’ and initial MH’s positions of the trajectories (Gaffney et al. 2007; Gaffney 2004). The probabilistic methodology and mixture model framework allow the component probability density function can be defined on non-vector data and to easily accommodate MH tracks of different lengths. Each trajectory (i.e., each MH track) is assumed to be generated by one of K different regression models. Each model gains its own shape parameters by the expectation maximization (EM) algorithm. The model is fit to the data by maximizing the likelihood of the parameters based on the MH tracks data. In other words, the assigned cluster has the highest posterior probability given the track. This clustering method has been applied to western North Pacific TCs (Camargo et al. 2007a, b; Mei and Xie 2016), the ENP TCs (Camargo et al. 2008), hurricanes in the Atlantic (Kossin et al. 2010) and TCs in the Southern Hemisphere (Ramsay et al. 2012).

In order to choose the most appropriate number of clusters for the ENP MH tracks in 1970–2020, we use the methods following from Camargo et al. (2018). We calculate log-likelihood and within cluster spread as the function of the number of clusters which is from 1 to 15. The log-likelihood is an important index that indicates how good the cluster analysis of MH tracks is in this probabilistic model and then can be used as a criterion to decide the most suitable number of clusters. Figure 

Fig. 15

a Log-likelihood values and within cluster spread for different number of clusters. The log-likelihood values are the maximum of 20 runs and the cluster spread values are the minimum of 20 runs, both obtained by a random permutation of the MHs given to the cluster model. b Maximum correlation among the clusters for each total cluster value, between NMH or ACE and JAS Niño3.4 in 1970–2020. Significant correlations are shown in black asterisk

15a shows that log-likelihood increases with the number of clusters, indicating that the larger the number of clusters is, the better the effect of MH tracks cluster is. But when the number of clusters exceeds a certain value (K ≥ 5), the goodness of cluster effect increases slowly. In addition, the within cluster spread curve indicates that the total dispersion of each type of MH track varies with cluster numbers. The smaller the value of within cluster spread is, the better the effect of MH tracks cluster is. Again, when the number of clusters exceeds a certain value (K ≥ 5), it shows no significant change within cluster spread. Therefore, we initially select the value that 3–5 as the candidates for the number of clusters.

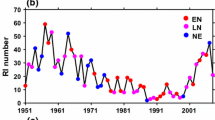
Further, in order to decide the most optimized number of clusters from 3 to 5, we examine the mean regression trajectories of MHs in 3, 4, and 5 clusters, respectively (not shown). When K is equal to 4 or 5, the mean regression trajectories of each cluster are complex and overlap. Because our work focuses on the relationship between the MHs activity and ENSO, we hope that the types of MHs associated with ENSO can be effectively stripped out by cluster analysis. The maximum correlation coefficient of annual number of MHs (NMH) or accumulated cyclone energy (ACE) and Niño3.4 index in July–September (JAS, major activity months of MHs in the ENP in Table 2) for each total cluster number is shown in Fig. 15b, indicating that when K = 3, the combination of two kinds of correlations is highest. Considering all the analysis above, the most appropriate number of clusters is chosen at 3 for this study, which is the same as Camargo et al. (2008).