Pricing, coalition stability, and profit allocation in the pull assembly supply chains under competition

Abstract

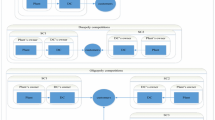
We consider a pull assembly supply chain consisting of an assembler and its multiple upstream component suppliers/subsidiaries, in which the former buys complementary components from these upstream component suppliers, assembles them into a final product, and sells the final product competing against another assembly firm (rival). The assembler decides the retail price competing with its rival and with the upstream component suppliers can freely decide whether or not to cooperate with another, which can eliminate horizontal and vertical inefficiencies within supply chain members. Using a stylized duopoly model, we study the optimal retail prices of the assembler and the optimal wholesale prices of these component suppliers under different alliance structures and analyze the coalition stability and profit allocation scheme via a proper transfer price for the assembly supply chain. We show that when the upstream suppliers are not allowed to form coalitions, the increase in the number of the upstream component suppliers trading with their assembler are a good thing for the two assemblers. In addition, increasing the intensity of price competition in the market induces the two assemblers to decline the retail prices and the upstream subsidiaries to cut down the wholesale prices; however, all the parties’ profits are not necessarily monotonic in this intensity. In environments in which the upstream subsidiaries can freely form coalitions, the above two results remain unchanged. We also find that the cooperation between the assembler and its upstream subsidiaries can always bring more profit and eliminate inefficiencies for the assembly supply chain. Importantly, we show that the constructed cooperative game has a non-empty core and can design a profit allocation scheme for the grand coalition based on the Shapley value. We identify the transfer prices of the assembler to the upstream subsidiaries to realize the profit allocation scheme that is fair and show that increasing the intensity of price competition can reduce the proposed Shapley values of the upstream suppliers and transfer prices.

Appendix: Technical proofs

Proof of Proposition 1

According to the arguments in Sect. 4.1, it is easy to show that

$$\begin{aligned}\frac{d p_A^{NC*}}{d \theta }=a(1+2n)\frac{-4(n+1)-(8n+12)\theta -(6n+9)\theta ^2}{\big ((2n+3)\theta ^2+8(n+1)\theta +4(n+1)\big )^2}<0,\end{aligned}$$

and $\frac{d p_B^{NC*}}{d \theta }=a\frac{-4(n+1)-(8n+12)(n+1)\theta -(2n+3)(4n+3)\theta ^2}{\big ((2n+3)\theta ^2+8(n+1)\theta +4(n+1)\big )^2}<0.$ Thus, for $l=A,B$, it directly follows that $\frac{d q_l^{NC*}}{d \theta }>0$, and $\frac{d w_A^{*}}{d \theta }=(1+2n)\frac{d p_A^{NC*}}{d \theta }<0$. Hence, the first part is proved.

We then show the second part. Note that for $i=1,2,...,n$, we have $\pi _A^{0*}=(1+n)\pi _A^{i*}$. Thus, we just need to prove the impact of $\theta$ on $\pi _A^{0*}$ and $\pi _B^{0*}$. By taking the first-order derivative of $\pi _A^{0*}$ with respect to $\theta$ and after some manipulations, we have $\frac{d \pi _A^{0*}}{d \theta }=-\theta (\theta -\theta _1(n))(\theta +\theta _1(n)),$ where $\theta _1(n)=\frac{-6+2\sqrt{9+3(n-1)(2n+3)}}{3(2n+3)}$. Clearly, $\pi _A^{0*}$ is a quasi-concave function of $\theta$; that is, if $\theta <\theta _1(n)$, $\pi _A^{0*}$ increases with $\theta$, and otherwise, $\pi _A^{0*}$ decreases with $\theta$. Similarly, it is also not difficult to derive that $\pi _B^{0*}$ is a quasi-concave function of $\theta$, which means that there exists a threshold value $\theta _2(n)(=\frac{4n^2-10n-12+4\sqrt{100n^4+268n^3+247n^2+87n+9}}{3(8n^2+18n+9)})$ such that, if $\theta <\theta _2(n)$, $\pi _B^{0*}$ increases with $\theta$, and otherwise, $\pi _B^{0*}$ decreases with $\theta$. Then, we complete the proof of Proposition 1. $\square$

Proof of Corollary 1

From the definitions of these two thresholds in Proposition 1, it is trivial to prove this corollary and we omit the details. $\square$

Proof of Proposition 2

Similarly with the proof of Proposition 1, it is not difficult to prove the first and second parts of Proposition 2. For the third part of this proposition, it is clear that $w_{Z_i}^{(N,k)*}$, $q_{A}^{(N,k)*}$ and $\pi _{Z_i}^{(N,k)*}$ are strictly decreasing in k. Taking the first-order derivative of $p_l^{(N,k)*}(l=A,B)$ with respect to k yields, $\frac{d p_A^{(N,k)*}}{d k}=\frac{a(2+3\theta )(2\theta ^2+8\theta +4)}{\big ((2n+3)\theta ^2+8(n+1)\theta +4(n+1)\big )^2}>0$ and $\frac{d p_B^{(N,k)*}}{d k}=\frac{a\theta (2\theta ^2+10\theta +6)}{\big ((2n+3)\theta ^2+8(n+1)\theta +4(n+1)\big )^2}>0.$ It directly follows that $\frac{d q_B^{(N,k)*}}{d k},~\frac{d \pi _B^{(N,k)*}}{d k}>0$. Similarly, it is easy to show that $\frac{d \pi _B^{(N,k)*}}{d k}<0$. Then, the proof is completed. $\square$

Proof of Corollary 2

From Proposition 2, we know that as the number of upstream-subsidiary alliance k increases, $p_{l}^{(N,k)*}$ and $\pi _{B}^{(N,k)*}$ increase, but $\pi _{Z_i}^{(N,k)*}$ and $\pi _{0}^{(N,k)*}$ decrease. Note that when $k=n$, this case is in fact the same as the one-player coalition case. Consequently, when $k<n$, we can derive the first part of Corollary 2. For the second part, it is not difficult to prove it according to the definitions of $\theta _A^{(N,k)}$ and $\theta _B^{(N,k)}$ in Proposition 2, and we omit the details of the proof. $\square$

Proofs of Proposition 3 and Corollary 3

With the proofs of Proposition 2 and Corollary 2, we can similarly prove the results in Proposition 3 and Corollary 3, and the fact that $\theta _l^{(N_0,k)}=\theta _l^{(N,t)}\big |_{t=k-1}$ where $\theta _l^{(N,t)}$ defined in Proposition 2. $\square$

Proof of Theorem 1

From Proposition 1, we known that for a given one-subsidiary coalition $\big \{j\big \}$, the profit of each coalition $\big \{j\big \}$ decreases with the number of subsidiaries in the coalition that all the other subsidiaries form. Therefore, all the other subsidiaries’ strategies affect the profit of the coalition $\big \{j\big \}$. However, Proposition 1 also shows that the coalition $\big \{j\big \}$ can achieve at least its profit in the case of a single-player alliance. Then, according to the definitions of the characteristic values of coalitions and the arguments in Sect. 4.1, it directly follows that

$$\begin{aligned}v(0)=\pi _A^{0*}=\frac{1+n}{1+\theta }\Big [\frac{a(2+5\theta +3\theta ^2)}{(2n+3)\theta ^2+8(n+1)\theta +4(n+1)}\Big ]^2,\end{aligned}$$

and for $i=1, 2, ..., n$, $v(i)=\pi _A^{i*}=\frac{1}{1+\theta }\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n+3)\theta ^2+8(n+1)\theta +4(n+1)}\Big )^2$. $\square$

Proof of Theorem 2

Note that for any $r\in (r=2,3, ..., n+1)$ and any $\mathbb {C}_r\subseteq N_0$, there are two possible situations, that is, $0\in \mathbb {C}_r$ and $0\notin \mathbb {C}_r$. Then we divide the analysis into two cases above.

Case 1: $0\in \mathbb {C}_r$. In this case, the given coalition $\mathbb {C}_r$ contains firm A; and thus, there are only $(n-r+1)$ upstream subsidiaries of firm A not belonging to the coalition $\mathbb {C}_r$. Clearly, the number of the upstream subsidiaries of firm A forming the alliance is at most $(n-r+2)$. From Proposition 3, it follows that the profit of coalition $\mathbb {C}_r$ decreases with the number of these possible coalitions. As a result, the profit that this coalition can be guaranteed to achieve is at least equal to the one that it can get when there are $(n-r+2)$ coalitions. Therefore, according to the definitions of the characteristic values of the coalitions and the results argued in Sect. 4.3, we have

$$\begin{aligned} v(\mathbb {C}_r)=\frac{n-r+2}{1+\theta }\cdot \Big [\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)}\Big ]^2. \end{aligned}$$

(9)

Case 2: $0\notin \mathbb {C}_r$. This means that firm A is not in the coalition $\mathbb {C}_r$. In this regard, there are $(n-r)$ subsidiaries of firm A not belonging to the coalition $\mathbb {C}_r$. It directly follows that the number of the coalitions of firm A forming an alliance is at most $(n-r+1)$. Following Proposition 2, which shows that the profit of coalition $\mathbb {C}_r$ decreases with the number of possible coalitions, we get that the profit that the coalition $\mathbb {C}_r$ is guaranteed to achieve is at least equal to the one that it can achieve when there are $(n-r+1)$ coalitions. Similar to the previous part, combining the definitions of the characteristic values of coalitions and the analysis in Sect. 4.2, we have

$$\begin{aligned} v(\mathbb {C}_r)=\frac{1}{1+\theta }\cdot \Big [\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)}\Big ]^2. \end{aligned}$$

(10)

Hence, we complete the proof. $\square$

Proof of Proposition 4

According to Theorem 2, (1) when $0\in \mathbb {C}_r$, by taking the first-order derivative of $v(\mathbb {C}_r)$ in Eq. (9), we have

$$\begin{aligned} \frac{d v(\mathbb {C}_r)}{d r}=\frac{a^2(2+5\theta +3\theta ^2)^2}{1+\theta }\cdot \frac{(2n-2r+3)\theta ^2+8(n-r+2)\theta +4(n-r+2)}{\left( (2n-2r+5)^2+8(n-r+2)\theta +4(n-r+2)\right) ^3}. \end{aligned}$$

Since $r\le n,$ $\frac{d v(\mathbb {C}_r)}{d r}>0$. This means that in this case, $v(\mathbb {C}_r)$ is an increasing function of r.

(2) When $0\notin \mathbb {C}_r$, it is easy to show that $g(n-r+1)$ is a decreasing function of r, where $g(n)=(2n+3)\theta ^2+8(n+1)\theta +4(n+1)$. It directly follows that $v(\mathbb {C}_r)$ in Eq. (10), which can be written as $\frac{a^2(2+5\theta +3\theta ^2)^2}{1+\theta }\cdot \frac{1}{(g(n-r+1))^2}$ is an increasing function of r. Therefore, the characteristic value $v(\mathbb {C}_r)$ increases with r, that is, the cooperative game $(N_0,v)$ is strictly increasing. $\square$

Proof of Proposition 5

For any coalition S, similar to the proof of Theorem 2, here we also divide the analysis into two cases, that is, $0\in S$ and $0\notin S$.

(1) For $0\in S$ and $i\in \{1, 2, ..., n\}$, suppose the size of coalition S is $|S|=r$, then we have

$$\begin{aligned}&v\left( S\bigcup \{i\}-v(S)\right) =v(\mathbb {C}_{r+1})-v(\mathbb {C}_r)\\&\quad =\frac{1}{1+\theta }\cdot \Big [(n-r+1)\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+3)\theta ^2+8(n-r+1)\theta +4(n-r+1)}\Big )^2\\&\qquad -(n-r+2)\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)}\Big )^2\Big ]. \end{aligned}$$

Let $H(r)=(1+\theta )(v(\mathbb {C}_{r+1})-v(\mathbb {C}_r))$. Thus, it is easy to show that $\frac{d H(r)}{d r}=h(r+1)-h(r)$, where

$$\begin{aligned} h(r)=\frac{(2n-2r+3)\theta ^2+8(n-r+2)\theta +4(n-r+2)}{\left( (2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)\right) ^3}. \end{aligned}$$

By taking the first-order derivative of h(r) with respect to r, we get

$$\begin{aligned} \frac{dh(r)}{dr}=\frac{8(\theta ^2+4\theta +2)\left( (n-r+1)\theta ^2+4(n+2-r)\theta +2(n+2-r)\right) }{\left( (2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)\right) ^4}>0, \end{aligned}$$

where the inequality holds since $r\le n$. This further implies that $h(r+1)-h(r)>0$. That is, $\frac{d H(r)}{dr}>0$. Hence, if $0\in S$, $v(S\bigcup \{i\}-v(S))$ is an increasing function of |S|.

(2) Next, for $0\notin S$, we have

$$\begin{aligned}&v\left( S\bigcup \{i\}-v(S)\right) =v(\mathbb {C}_{r+1})-v(\mathbb {C}_r)\\&\quad =\frac{1}{1+\theta }\cdot \Big [\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+3)\theta ^2+8(n-r+1)\theta +4(n-r+1)}\Big )^2\\&\qquad -\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)}\Big )^2\Big ]. \end{aligned}$$

Similarly with the analysis in part (1), it is not difficult to show that $v(S\bigcup \{i\}-v(S))$ is a decreasing function of |S|. $\square$

Proof of Theorem 3

By the definition of the Shapley value in Shapley (1953) and Myerson (1991), the Shapley value of firm A in the cooperative game $(N_0, v)$ is given as

$$\begin{aligned} \begin{aligned} Y_{0}^{n}&=\sum \limits _{S\subseteq {{N}_{0}}\backslash D}{\frac{\left| S \right| !\left( \left| {{N}_{0}} \right| -\left| S \right| -1 \right) !}{\left| {{N}_{0}} \right| !}}\left( v\left( S\bigcup \{D\} \right) -v\left( S \right) \right) \\&=\sum \limits _{r=1}^{n}{C_{n}^{r}\frac{r!\cdot \left( n-r \right) !}{(n+1)!}}\left( v\left( {{\mathbb {C}}_{r}}\bigcup \{D\} \right) -v\left( {{\mathbb {C}}_{r}} \right) \right) +C_{n}^{0}\frac{0!\cdot n!}{(n+1)!}\left( v\left( D \right) -v\left( \varnothing \right) \right) \\&=\sum \limits _{r=1}^{n}{\frac{1}{n+1}}\cdot \left( v\left( {{\mathbb {C}}_{r}}\bigcup \{D\} \right) -v\left( {{\mathbb {C}}_{r}} \right) \right) +\frac{1}{n+1}v\left( D \right) \\&=\frac{1}{(1+n)(1+\theta )}\cdot \left[ \Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2+\sum _{j=1}^n j \Big (\frac{a(2+5\theta +3\theta ^2)}{(2j+3)\theta ^2+8(j+1)\theta +4(j+1)}\Big )^2\right] . \end{aligned} \end{aligned}$$

(11)

Due to the symmetry of the upstream subsidiaries, the Shapley values of the upstream subsidiaries should satisfy $Y_{1}^{n}=Y_{2}^{n}= \cdots =Y_{n}^{n}$. Since the profit of the assembly supply chain with firm A is $v({{N}_{0}})=\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2$, the upstream subsidiaries $U_i(i = 1,2,...,n)$ are as follows:

$$\begin{aligned}&Y_{i}^{n}=\frac{v(N_0)-Y_{0}^{n}}{n} =\frac{1}{1+\theta }\cdot \frac{1}{n(1+n)(1+\theta )}\cdot \\&\quad \left[ n\Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2-\sum _{j=1}^n j \Big (\frac{a(2+5\theta +3\theta ^2)}{(2j+3)\theta ^2+8(j+1)\theta +4(j+1)}\Big )^2\right] \end{aligned}$$

for $i=1,2,...,n$. Then, we complete the proof of this theorem. $\square$

Proof of Lemma 1

With the definition of ${{\varphi }_{1}}(r+1,n)$, we have, after some manipulations,

$$\begin{aligned}&{{\varphi }_{1}}(r+1,n)-{{\varphi }_{1}}(r,n)=Y_{i}^{n}-\frac{1}{1+\theta }\cdot \Big [\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+3)\theta ^2+8(n-r+1)\theta +4(n-r+1)}\Big )^2\nonumber \\&\quad -\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+5)\theta ^2+8(n-r+2)\theta +4(n-r+2)}\Big )^2\Big ]. \end{aligned}$$

(12)

From Theorem 3, it follows that the Shapley values of the upstream subsidiaries are not associated with r. Then, with the proof of the second part of Proposition 5, which can show that the second term in Eq. (12) decreases with r Thus, ${{\varphi }_{1}}(r+1,n)-{{\varphi }_{1}}(r,n)$ is an increasing function of r. On the other hand, by some manipulations on the difference of ${{\varphi }_{2}}(r+1,n)$ and ${{\varphi }_{2}}(r,n)$, we have

$$\begin{aligned} \begin{aligned}&{{\varphi }_{2}}(r+1,n)-{{\varphi }_{2}}(r,n) =Y_{i}^{n}-\frac{1}{1+\theta }\cdot \Big [(n-r)\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+1)\theta ^2+8(n-r)\theta +4(n-r)}\Big )^2\\&\quad -(n-r+1)\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n-2r+3)\theta ^2+8(n-r+1)\theta +4(n-r+1)}\Big )^2\Big ]. \end{aligned} \end{aligned}$$

(13)

Then, according to the first part of Proposition 5, which can show that the second term in Eq. (13) increases with r, it directly follows that ${{\varphi }_{2}}(r+1,n)-{{\varphi }_{2}}(r,n)$ is a decreasing function of r. $\square$

Proof of Lemma 2

We sufficiently show the proof of the first part, and the second part can be proven similarly. By the mathematical induction, we begin with showing that for $n=2,3,...$, ${{\varphi }_{1}}(1,n)\ge 0.$ When $n=2$, we have

$$\begin{aligned} \begin{array}{ll} \varphi _{1}(1,2)&{}= Y_{i}^{2}-\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{7\theta ^2+24\theta +12}\Big )^2\\ &{}=\frac{a^2(2+5\theta +3\theta ^2)^2}{1+\theta }\cdot \frac{7936+63488\theta +206336{{\theta }^{2}}+349184{{\theta }^{3}}+328512{{\theta }^{4}}+171264{{\theta }^{5}}+47280{{\theta }^{6}}+5984{{\theta }^{7}}+209{{\theta }^{8}}}{6(3\theta ^2+8\theta +4)^2(5\theta ^2+16\theta +8)^2(7\theta ^2+24\theta +12)^2}, \end{array} \end{aligned}$$

which is always positive. Suppose that for $n=m$, $\varphi _{1}(1,m)>0$. Thus, it follows that

$$\begin{aligned}\varphi _{1}(1,m)&=Y_{i}^{m}-\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+3) \theta ^2+8(m+1)\theta +4(m+1)}\Big )^2\nonumber \\&=\frac{1}{(m^2+m)(1+\theta )}\cdot \Big [m\Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2\\&\quad -\sum \limits _{j=1}^{m}j\Big (\frac{a(2+5\theta +3\theta ^2)}{(2j+3)\theta ^2+8(j+1)\theta +4(j+1)}\Big )^2\Big ]\\&\quad -\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+3)\theta ^2+8(m+1)\theta +4(m+1)}\Big )^2 \ge 0, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&\frac{m}{(3\theta ^2+8\theta +4)^2}-\frac{m(m+1)}{((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2}\nonumber \\&\quad \ge \sum \limits _{j=1}^{m}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}. \end{aligned}$$

(14)

Next, we need to show that it holds for $n=m+1$. To do this, when $n=m+1$, we have

$$\begin{aligned} \begin{array}{ll} &{}\varphi _{1}^{(1,m+1)} =Y_{i}^{m+1}-\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+5)\theta ^2+8(m+2)\theta +4(m+2)}\Big )^2\\ &{}\quad = \frac{1}{(1+\theta )(m+2)}\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2-\frac{1}{(m+1)(m+2)(1+\theta )}\cdot \Big (-\sum \limits _{j=1}^{m}j\Big (\frac{a(2+5\theta +3\theta ^2)}{(2j+3)\theta ^2+8(j+1)\theta +4(j+1)}\Big )^2\\ &{}\qquad -(m+1)\Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+5)\theta ^2+8(m+2)\theta +4(m+2)}\Big )^2\Big )-\frac{1}{1+\theta }\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+5)\theta ^2+8(m+2)\theta +4(m+2)}\Big )^2\\ &{}\quad \ge \frac{1}{(1+\theta )(m+2)}\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2+\frac{m}{(m+2)(1+\theta )}\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+3)\theta ^2+8(m+1)\theta +4(m+1)}\Big )^2\\ &{}\qquad -\frac{m+3}{(m+2)(1+\theta )}\cdot \Big (\frac{a(2+5\theta +3\theta ^2)}{(2m+5)\theta ^2+8(m+2)\theta +4(m+2)}\Big )^2\\ &{}\quad =\frac{1}{1+\theta } \frac{a^2(2+5\theta +3\theta ^2)^2({{F}_{1}}{{m}^{4}}+{{F}_{2}}{{m}^{3}}+{{F}_{3}}{{m}^{2}}+{{F}_{4}}m+{{F}_{5}})}{(m+1)(m+2)(3\theta ^2+8\theta +4)^2(2m+3)\theta ^2+8(m+1)\theta +4(m+1)^2(2m+5)\theta ^2+8(m+2)\theta +4(m+2)^2} \\ &{}\quad \ge 0, \end{array} \end{aligned}$$

where the first inequality holds because of the fact in Eq. (14), and

$$\begin{aligned}{} & {} F_{1}=256+2048\theta +6656{{\theta }^{2}}+11264{{\theta }^{3}}+10624{{\theta }^{4}}+5632{{\theta }^{5}}+1664{{\theta }^{6}}+256{{\theta }^{7}}+16{{\theta }^{8}} \\{} & {} F_{2}=1280+10240\theta +33408{{\theta }^{2}}+57088{{\theta }^{3}}+54832{{\theta }^{4}}+29888{{\theta }^{5}}+9104{{\theta }^{6}}\\{} & {} \qquad +1440{{\theta }^{7}}+92{{\theta }^{8}}, \\{} & {} F_{3}=2304+18432\theta +60288{{\theta }^{2}}+103680{{\theta }^{3}}+100704{{\theta }^{4}}+55680{{\theta }^{5}}+17072{{\theta }^{6}}\\{} & {} \qquad +2656{{\theta }^{7}}+160{{\theta }^{8}}, \\{} & {} F_{4}=1536+12288\theta +40192{{\theta }^{2}}+69120{{\theta }^{3}}+67024{{\theta }^{4}}+36672{{\theta }^{5}}+10784{{\theta }^{6}}\\{} & {} \qquad +1472{{\theta }^{7}}+57{{\theta }^{8}}, \\{} & {} F_{5}=256+2048\theta +6656{{\theta }^{2}}+11264{{\theta }^{3}}+10544{{\theta }^{4}}+5312{{\theta }^{5}}+1240{{\theta }^{6}}+48{{\theta }^{7}}-18{{\theta }^{8}}. \end{aligned}$$

Similarly, for $r=2,3,...$, and $n=2,3,...$, we can prove that $\varphi _1(r,n)\ge 0$.

Then we prove that for $n=2,3,...$, $\varphi _1(2,n)-\varphi _1(1,n)\ge 0$. For $n=2$, on one hand, we have

$$\begin{aligned} \begin{array}{ll} &{}{{\varphi }_{1}}(2,2)-{{\varphi }_{1}}(1,2)=\frac{1}{6+6\theta }\Big [\Big (\frac{a(2+5\theta +3\theta ^2)}{3\theta ^2+8\theta +4}\Big )^2-\Big (\frac{a(2+5\theta +3\theta ^2)}{5\theta ^2+16\theta +8}\Big )^2 -2\Big (\frac{a(2+5\theta +3\theta ^2)}{7\theta ^2+24\theta +12}\Big )^2\Big ]\\ &{}\qquad -\frac{1}{1+\theta }\Big [\Big (\frac{a(2+5\theta +3\theta ^2)}{5\theta ^2+16\theta +8}\Big )^2-\Big (\frac{a(2+5\theta +3\theta ^2)}{7\theta ^2+24\theta +12}\Big )^2\Big ] \\ &{}\quad =\frac{a^2(2+5\theta +3\theta ^2)^2}{1+\theta }\cdot \frac{6400+51200\theta +166400{{\theta }^{2}}+2816000{{\theta }^{3}}+265152{{\theta }^{4}}+139008{{\theta }^{5}}+39312{{\theta }^{6}}+5408{{\theta }^{7}}+263{{\theta }^{8}}}{6(3\theta ^2+8\theta +4)^2(5\theta ^2+16\theta +8)^2(7\theta ^2+24\theta +12)^2}. \end{array} \end{aligned}$$

It is clear that ${{\varphi }_{1}}(2,2)-{{\varphi }_{1}}(1,2)\ge 0$. On the other hand, for $n=3, 4, ...$, we get that,

$$\begin{aligned}&{{\varphi }_{1}}(2,n)-{{\varphi }_{1}}(1,n)=Y_{i}^{n}-\frac{1}{1+\theta }\cdot \Big [\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n+1)\theta ^2+8n\theta +4n}\Big )^2\\&\quad -\Big (\frac{a(2+5\theta +3\theta ^2)}{(2n+3)\theta ^2+8(n+1)\theta +4(n+1)}\Big )^2 \Big ]. \end{aligned}$$

Note that for any given $\theta$ and $n=3, 4, ...$, $\frac{1}{((2n+1)\theta ^2+8n\theta +4n)^2}-\frac{2}{((2n+3)\theta ^2+8(n+1)\theta +4(n+1))^2}\le 0$. As a result, it is not difficult to show that $\varphi _{1}(2,n)-\varphi _{1}(1,n)\ge 0$. With the results above, the proof of Lemma 2 is completed. $\square$

Proof of Theorem 4

With the definition of the core of the game (N, v) in Eq. (5), we sufficiently need to prove that $\sum \limits _{i\in S}{Y_{i}^{n}}\ge v(S)$, for $\forall S\subseteq {{N}_{0}}$; that is, the individual or collective rationality holds, since the Shapley value $Y_{i}^{n}$ satisfies the efficiency: $\sum \limits _{i\in {{N}_{0}}}{Y_{i}^{n}}=v({{N}_{0}})$. As such, for any $S\subseteq N_0$, there are only two possible cases, i.e., $0\notin S$ and $0\in S$.

Case 1: $0\notin S$. In this case, if $|S|=1$, by Lemma 2(i), it follows that $\sum \limits _{i\in S}{Y_{i}^{n}}\ge v(S)$. If $n\ge |S|>1$, then $\sum \limits _{i\in S}{Y_{i}^{n}}\ge v(S)$ can be derived directly from Lemma 2(ii) (for the details, see the proof of Lemma 2).

Case 2: $0\in S$. Then, if $|S|=1$, we need to prove $Y_{0}^{n}\ge v(\{0\})$; that is,

$$\begin{aligned}&\frac{1}{n+1}\Big (\frac{1}{(3\theta ^2+8\theta +4)^2}+\sum \limits _{j=1}^{n}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}\Big )\\&\quad \ge \frac{1+n}{((2n+3)\theta ^2+8(n+1)\theta +4(n+1))^2}, \end{aligned}$$

which can be shown by the following mathematical induction. When $n=2$, it follows that

$$\begin{aligned} \begin{array}{ll} &{}Y_{0}^{2}-v(\{0\}) =\frac{1}{3}\Big (\frac{1}{(3\theta ^2+8\theta +4)^2}+\frac{1}{(5\theta ^2+16\theta +8)^2} +\frac{2}{(7\theta ^2+24\theta +12)^2}\Big )-\frac{3}{(7\theta ^2+24\theta +12)^2}\\ &{}\quad =\frac{4352+34816\theta +113152{{\theta }^{2}}+191488{{\theta }^{3}}+180096{{\theta }^{4}}+93696{{\theta }^{5}}+25632{{\theta }^{6}}+3136{{\theta }^{7}}+91{{\theta }^{8}}}{3(3\theta ^2+8\theta +4)^2(5\theta ^2+16\theta +8)^2(7\theta ^2+24\theta +12)^2}. \end{array} \end{aligned}$$

Obviously, the above result holds for $n=2$. Suppose it holds for $n=m$, that is, assume that

$$\begin{aligned}&\frac{1}{m+1}\Big (\frac{1}{(3\theta ^2+8\theta +4)^2}+\sum \limits _{j=1}^{m}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}\Big )\\&\quad \ge \frac{1+m}{((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2}. \end{aligned}$$

Then when $n=m+1$, we have

$$\begin{aligned} \begin{aligned}&\frac{1}{m+2}\Big (\frac{1}{(3\theta ^2+8\theta +4)^2}+\sum \limits _{j=1}^{m}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}\\&\qquad\quad + \frac{1+m}{((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2}\Big )\\&\qquad\quad -\frac{m+2}{((2m+5)\theta ^2+8(m+2)\theta +4(m+2))^2} \\&\quad\quad \ge \frac{1}{m+2}\Big ( \frac{{{(m+1)}^{2}}}{((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2}\\&\quad\qquad +\frac{m+1}{((2m+5)\theta ^2+8(m+2)\theta +4(m+2))^2} \Big )\\&\quad\qquad -\frac{m+2}{((2m+5)\theta ^2+8(m+2)\theta +4(m+2))^2}\\&\quad\quad =\frac{1}{m+2}\Big ( \frac{{{(m+1)}^{2}}}{((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2}\\&\quad\qquad -\frac{m^2+3m+3}{((2m+5)\theta ^2+8(m+2)\theta +4(m+2))^2} \Big )\\&\quad\quad =\frac{{{G}_{1}}{{m}^{3}}+{{G}_{2}}{{m}^{2}}+{{G}_{3}}m+{{G}_{4}}}{(m+2)((2m+3)\theta ^2+8(m+1)\theta +4(m+1))^2((2m+5)\theta ^2+8(m+2)\theta +4(m+2))^2}\\&\quad\quad \ge 0, \end{aligned} \end{aligned}$$

(15)

where ${{G}_{1}}=16+64\theta +80{{\theta }^{2}}+32{{\theta }^{3}}+4{{\theta }^{4}}$, ${{G}_{2}}=48+192\theta +240{{\theta }^{2}}+96{{\theta }^{3}}+12{{\theta }^{4}}$, ${{G}_{3}}=48+192\theta +232{{\theta }^{2}}+80{{\theta }^{3}}+7{{\theta }^{4}}$, and ${{G}_{4}}=16+64\theta +72{{\theta }^{2}}+16{{\theta }^{3}}-2{{\theta }^{4}}$. Hence, we can obtain that $Y_{0}^{n}\ge v(\{0\})$.

In addition, if $n+1\ge |S|>1$, we just need to prove that $Y_{0}^{n}+\sum \limits _{i\in S\backslash \{0\}}{Y_{i}^{n}}\ge v(S)$. Let $|S|=r+1$, then it is sufficient to prove that

$$\begin{aligned}&\frac{1}{n+1}\Big (\frac{1}{(3\theta ^2+8\theta +4)^2}+\sum \limits _{j=1}^{n}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}\Big )\\&\quad\qquad +\frac{r}{n(n+1)}\Big (\frac{n}{(3\theta ^2+8\theta +4)^2}-\sum \limits _{j=1}^{n}\frac{j}{((2j+3)\theta ^2+8(j+1)\theta +4(j+1))^2}\Big )\\&\quad\quad \ge \frac{n-r+1}{((2n-2r+3)\theta ^2+8(n-r+1)\theta +4(n-r+1))^2}, \end{aligned}$$

which means that, to show this inequality, we need to prove ${{\varphi }_{2}}(r,n)\ge 0$. According to Lemma 1, ${{\phi }_{2}}(r,n)\doteq {{\varphi }_{2}}(r+1,n)-{{\varphi }_{2}}(r,n)$ is a decreasing function of r. Then, ${{\phi }_{2}}(r,n)$ has three possible cases: (1) ${{\phi }_{2}}(r,n)\ge 0$, for all $r=1, 2, \cdots , n$; (2) ${{\phi }_{2}}(r,n)\le 0$, for all $r=1, 2, \cdots , n$; (3) there exists ${{r}^{*}}\in \big \{1, 2, \cdots , n\big \}$, ${{\phi }_{2}}(r,n)\ge 0$ for $r=1, 2,\cdots , {{r}^{*}}$ and ${{\phi }_{2}}(r,n)\le 0$ for $r={{r}^{*}},{{r}^{*}}+1, \cdots , n$. In any of the three cases, following Lemma 2(ii), and ${{\varphi }_{2}}(n,n)=0$, we can get that for $r=1, 2, \cdots , n,~n=2, 3,\cdots$, ${{\varphi }_{2}}(r,n)\ge 0$. Therefore, we have $Y_{0}^{n}+\sum \limits _{i\in S\backslash \{0\}}{Y_{i}^{n}}\ge v(S)$.

With the arguments above, one can easily see that the Shapley value $\{Y_{i}^{n},i=0, 1, 2, \cdots , n\}$ is in the core of the cooperative game $(N_0, v)$. $\square$

Proof of Theorem 5

According to the allocation rule generated by Theorem 4, it is not difficult to derive the transfer prices between firm A and each upstream subsidiary $U_i(i = 1,2,...,n)$. $\square$