Backpropagation of neural network dynamical models applied to flow control

Abstract

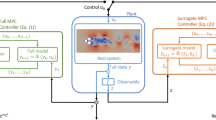
Backpropagation of neural network models (NNMs) is applied to control nonlinear dynamical systems using several different approaches. By leveraging open-loop data, we show the feasibility of building surrogate models with control inputs that are able to learn important features such as types of equilibria, limit cycles and chaos. Two novel approaches are presented and compared to gradient-based model predictive control (MPC): the neural network control (NNC), where an additional neural network is trained as a control law in a recurrent fashion using the nonlinear NNMs, and linear control design, enabled through linearization of the obtained NNMs. The latter is compared with dynamic mode decomposition with control (DMDc), which also relies on a data-driven linearized model. It is shown that the linearized NNMs better approximate the systems’ behavior near an equilibrium point than DMDc, particularly in cases where the data display highly nonlinear characteristics. The proposed control approaches are first tested on low-dimensional nonlinear systems presenting dynamical features such as stable and unstable limit cycles, besides chaos. Then, the NNC is applied to the nonlinear Kuramoto–Sivashinsky equation, exemplifying the control of a chaotic system with higher dimensionality. Finally, the proposed methodologies are tested on the compressible Navier–Stokes equations. In this case, the stabilization of a cylinder vortex shedding is sought using different actuation setups by taking measurements of the lift force with delay coordinates.

Graphic abstract

Appendices

Appendix A: Datasets

The datasets used to train the dynamical models are provided as a supplemental material. These sets are referenced along the following files:

• data_nn_lv.txt: Lotka–Volterra training data.

• data_nn_vp.txt: Van der Pol training data.

• data_nn_li.txt: Liénard training data.

• data_nn_lo.txt: Lorenz training data.

• data_nn_ks.txt: Kuramoto–Sivashinsky training data.

• data_dmdc_lv.txt: Alternate training data for Lotka–Volterra. This dataset was built with very small control inputs, so the system response is approximately linear. This is done in order to show that DMDc provides good models for nearly linear systems (see Appendix D). In cases where the operating point is unstable, building such type of dataset is not possible, as shown in the Van der Pol and Lorenz examples.

• data_nn_cyljet_01.txt - data_nn_cyljet_11.txt: Data used for blowing/suction actuated cylinder flow.

• data_nn_cylrot_01.txt - data_nn_cylrot_20.txt: Data used for rotation actuated cylinder flow.

All datasets are organized in text files containing $1+m+n$ columns. The first column corresponds to the dimensionless time array. The next m columns are the control input values, and the last n columns contain the states. In all cases studied in this work $m=1$ and, therefore, the second column represents the only control input.

Appendix B: Training of neural network models

The datasets employed for training the neural network (NN) dynamical models are referenced here and provided as supplementary material. Tables 1 and 2 present the hyperparameters chosen for each trained model.

Table 1 Hyperparameters used in the NNMs. All networks are trained using the ReLU activation function and the ADAM optimizer with a constant learning rate

Table 2 Hyperparameters used in the NNMs for cylinder flows. All networks are trained using the ReLU activation function and the ADAM optimizer with a constant learning rate

Appendix C: Control parameters

Table 3 presents the chosen control parameters for each technique and system studied. NNC training for the low-order systems is performed by gathering data randomly sampled from a normal distribution to build ${\textbf{X}}_0$. For the Kuramoto–Sivashinsky (KS) equation, the data are the same one used to train the NNM (Dataset 5). Therefore, the distribution parameters for the KS case are not applicable (N/A).

Table 4 presents values of hyperparameters used in NNC for cylinder flows. In these cases, instead of using a random dataset for training the controller, datasets built from open-loop simulations are used. The specific file used in each case is pointed in the table. For the linear control case applied to the cylinder flow, the control saturation is set to 0.4 rad/s$^2$. Figure 12 presents the chosen closed-loop poles for stabilization.

Table 3 Control parameters employed in the solution of different dynamical systems for different techniques

Table 4 NNC hyperparameters used in cylinder flows

Fig. 12

Pole map for the linearized cylinder flow model. The closed-loop poles are placed inside the unit circle aiming stabilization

Appendix D: Dynamic mode decomposition with control

We compare control results from pole placement through the linearized NNM with dynamic mode decomposition with control (DMDc) [34]. A data matrix

$$\begin{aligned} \varvec{\Omega } = \begin{bmatrix} {\textbf{X}} \\ \varvec{\Upsilon } \end{bmatrix} \end{aligned}$$

(27)

is built, where ${\textbf{X}}$ and $\varvec{\Upsilon }$ correspond to the states and the control inputs, respectively, as follows:

$$\begin{aligned} {\textbf{X}}&=\begin{bmatrix} \text {|} &{} \text {|} &{} &{} \text {|}\\ {\textbf{x}}_0 &{} {\textbf{x}}_1 &{} \dots &{} {\textbf{x}}_{q-1}\\ \text {|} &{} \text {|} &{} &{} \text {|}\\ \end{bmatrix}, \end{aligned}$$

(28)

$$\begin{aligned} \varvec{\Upsilon }&=\begin{bmatrix} \text {|} &{} \text {|} &{} &{} \text {|}\\ {\textbf{u}}_0 &{} {\textbf{u}}_1 &{} \dots &{} {\textbf{u}}_{q-1}\\ \text {|} &{} \text {|} &{} &{} \text {|}\\ \end{bmatrix}. \end{aligned}$$

(29)

Here, q is the number of sampled snapshots. A delayed states matrix ${\textbf{X}}'$ is also built as

$$\begin{aligned} {\textbf{X}}'=\begin{bmatrix} \text {|} &{} \text {|} &{} &{} \text {|}\\ {\textbf{x}}_1 &{} {\textbf{x}}_2 &{} \dots &{} {\textbf{x}}_{q}\\ \text {|} &{} \text {|} &{} &{} \text {|}\\ \end{bmatrix}\text{. } \end{aligned}$$

(30)

Since no dimensionality reduction is needed for the current problem, we simply estimate

$$\begin{aligned} {\textbf{X}}'=\begin{bmatrix} {\textbf{A}}&{\textbf{B}} \end{bmatrix} = {\textbf{X}}'{\textbf{G}}^\dagger \text{. } \end{aligned}$$

(31)

Figure 13 presents results for three of the systems studied in this work. For the Lotka–Volterra equations, we build a new data set with very small control inputs (Dataset 6) (although the NNM is still the same shown in the main text, which is trained with Dataset 1). This is done in order to sample a nearly linear response. The datasets for the Van der Pol and Lorenz systems are the same ones used for training the NNMs (Datasets 2 and 5). In such cases, due to the unstable equilibrium points, even small perturbations would imply in responses that grow until nonlinearities are activated. Since the Lorenz system dataset is built from highly nonlinear responses, the control design based on the model obtained with DMDc does not work well. In the examples shown in Fig. 13, the gain matrices obtained through pole placement using the DMDc and the linearized NNMs are used to compute the closed-loop poles of an analytical linearization. The comparison shows that DMDc works better for linear systems and starts to fail when nonlinearities are more prominent. Table 5 presents the resulting ${\textbf{A}}$ and ${\textbf{B}}$ matrices found through each method. An analytical version is also presented as reference, which is computed directly through differentiation of the ordinary differential equations.

Fig. 13

Comparison of linear models. The closed-loop poles are calculated through the eigenvalues of $A-BK$, where A and B are relative to the analytically linearized model and the gain matrix K results from pole placement design using the other models (DMDc and NNM linearization). At the bottom row, the thin lines show the responses for the systems with controllers designed using the linearized NNMs. The thick (thin) lines refer to compensators obtained by the DMDc (NN)

Table 5 Comparison of linearized models

Appendix E: Computational costs

Figure 14 presents a comparison of time per iteration for different values of $n_h$ for the proposed Lotka–Volterra model with the other control parameters set as in case II. It depicts both nonlinear techniques studied in this work, MPC and NNC. For the tested $n_h$ values, the MPC cost grows approximately linearly. Since only a direct evaluation of the NNC is required after training, the cost does not change as $n_h$ grows. Also, further reduction in evaluation times could be achieved by implementing the trained NNC in a compiled software for real world applications. In the present work, $n_h$ is chosen by trial and error avoiding very small values that would compromise control performance as well as excessively large values, which would make the training process expensive. To illustrate the relevance of not using very small values of $n_h$, Fig. 15 presents a comparison of the responses to different horizon lengths using NNC. For small values of $n_h$, the system performance is compromised. The figure also shows that the response improvements are not significant after a certain value, i.e., a large value of $n_h$ will only impact the training cost (or the evaluation cost in case of MPC).

Fig. 14

Time per control iteration as a function of the discrete horizon $n_h$

Fig. 15

Lotka–Volterra system response to NNC with different values of the time horizon $n_h$. The responses show are computed by simulating the NNMs in closed loop

Appendix F: Results for cylinder flow ROM

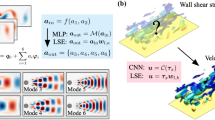
This appendix presents the complete responses for the cases studied in Sect. 4.3.1. The temporal evolution of the 12 POD modes is shown in Figs. 16 and 17.

Fig. 16

ROM-controlled response where ${\tilde{F}}$ learns the dynamics of mode $x_1$ through its time delays. The vertical dashed line indicates when the controller is turned on. Complete convergence is not achieved

Fig. 17

ROM-controlled response where ${\tilde{F}}$ learns the dynamics of modes $x_1$ and $x_6$ through their time delays. The vertical dashed line indicates when the controller is turned on. The modes converge as the system is stabilized