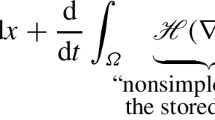Skip to main content
SpringerLink
Log in

Visco-elastodynamics at large strains Eulerian

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

Isothermal visco-elastodynamics in the Kelvin–Voigt rheology is formulated in the spatial Eulerian coordinates in terms of velocity and deformation gradient. A generally nonconvex (possibly also frame-indifferent) stored energy is admitted. The model involves a nonlinear 2nd-grade nonsimple (multipolar) viscosity so that the velocity field is well regular. To simplify analytical arguments, volume variations of the solid material are assumed to be only rather small so that the mass density is constant, exploiting the concept of semi-compressible materials. Existence of weak solutions is proved by using the Galerkin method combined with a suitable regularization, using nontrivial results about transport by smooth velocity fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Antman, S.S.: Physically unacceptable viscous stresses. Zeitschrift Angew. Math. Phys. 49, 980–988 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  2. Ball, J.M.: Global invertibility of Sobolev functions and the interpenetration of matter. Proc. R. Soc. Edinb., Sect.A 88, 315–328 (1981)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ball, J.M.: Some open problems in elasticity. In: Newton, P., Holmes, P., Weinstein, A. (eds.) Geometry, Mechanics, and Dynamics, pp. 3–59. Springer, New York (2002)

    Chapter  Google Scholar 

  4. Ball, J.M.: Progress and puzzles in nonlinear elasticity. In Poly-, Quasi- and Rank-One Convexity in Applied Mechanics (Eds.: Schröder, J., Neff, P.:), CISM Intl. Centre for Mech. Sci. 516, pp. 1–15. Springer, Wien (2010)

  5. Bellout, H., Bloom, F., Nečas, J.: Phenomenological behavior of multipolar viscous fluids. Qarterly Appl. Math. 1, 559–583 (1992)

    MathSciNet  MATH  Google Scholar 

  6. Benešová, B., Forster, J., Liu, C., Schlömerkemper, A.: Existence of weak solutions to an evolutionary model for magnetoelasticity. SIAM J. Math. Anal. 50, 1200–1236 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  7. Brenner, H.: Kinematics of volume transport. Phys. A 349, 11–59 (2005)

    Article  Google Scholar 

  8. Brenner, H.: Fluid mechanics revisited. Phys. A 349, 190–224 (2006)

    Article  Google Scholar 

  9. Chen, Y., Zhang, P.: The global existence of small solutions to the incompressible viscoelastic fluid system in 2 and 3 space dimensions. Commun. Partial Differ. Eqs. 31, 1793–1810 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  10. Dafermos, C., Hrusa, W.: Energy methods for quasilinear hyperbolic initial-boundary value problems. Applications to elastodynamics. Arch. Ration. Mech. Anal. 87, 267–292 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  11. Davoli, E., Roubíček, T., Stefanelli, U.: A note about hardening-free viscoelastic models in Maxwellian-type rheologies. Math. Mech. Solids 26, 1483–1497 (2021)

    Article  MathSciNet  Google Scholar 

  12. Demoulini, S.: Weak solutions for a class of nonlinear systems of viscoelasticity. Arch. Rational Mech. Anal. 155, 299–334 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  13. Demoulini, S., Stuart, D.M.A., Tzavaras, A.E.: A variational approximation scheme for three-dimensional elastodynamics with polyconvex energy. Arch. Rational Mech. Anal. 157, 325–344 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  14. Demoulini, S., Stuart, D.M.A., Tzavaras, A.E.: Weak-strong uniqueness of dissipative measure-valued solutions for polyconvex elastodynamics. Arch. Rational Mech. Anal. 205, 927–961 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Emmrich, E., Puhst, D.: Measure-valued and weak solutions to the nonlinear peridynamic model in nonlocal elastodynamics. Nonlinearity 28, 285–307 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Emmrich, E., Puhst, D.: Survey of existence results in nonlinear peridynamics in comparison with local elastodynamics. Comput. Methods Appl. Math. 15, 483–496 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  17. Fosdick, R., Royer-Carfagni, G.: The Lagrange multipliers and hyperstress constraint reactions in incompressible multipolar elasticity theory. J. Mech. Phys. Solids 50, 1627–1647 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  18. Fried, E., Gurtin, M.E.: Tractions, balances, and boundary conditions for nonsimple materials with application to liquid flow at small-length scales. Arch. Rational Mech. Anal. 182, 513–554 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  19. Giga, M.-H., Kirshtein, A., Liu, C.: Variational modeling and complex fluids. In: Novotný, A., Giga, Y. (eds.) Handbook of Mathematical Analysis in Mechanics of Viscous Fluids, pp. 1–41. Springer, Cham (2017)

    Google Scholar 

  20. Gurtin, M.E.: Topics in Finite Elasticity. SIAM, Philadelphia (1983)

    MATH  Google Scholar 

  21. Gurtin, M.E., Fried, E., Anand, L.: The Mechanics and Thermodynamics of Continua. Cambridge University Press, New York (2010)

    Book  Google Scholar 

  22. Healey, T.J., Krömer, S.: Injective weak solutions in second-gradient nonlinear elasticity. ESAIM: Control Optim. Cal. Var. 15, 863–871 (2009)

    MathSciNet  MATH  Google Scholar 

  23. Hu, X., Lin, F.: Global solutions of two-dimensional incompressible viscoelastic flows with discontinuous initial data. Commun. Pure Appl. Math. 69, 372–404 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  24. Hu, X., Wang, D.: Global existence for the multi-dimensional compressible viscoelastic flows. J. Differ. Equ. 250, 1200–1231 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Hughes, T.J.R., Kato, T., Marsden, J.E.: Well-posed quasi-linear second-order hyperbolic systems with applications to nonlinear elastodynamics and general relativity. Arch. Rational Mech. Anal. 63, 273–294 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  26. Kalousek, M., Kortum, J., Schlömerkemper, A.: Mathematical analysis of weak and strong solutions to an evolutionary model for magnetoviscoelasticity. Discrete Contin. Dyn. Syst. 14, 17–39 (2021)

    MathSciNet  MATH  Google Scholar 

  27. Koumatos, K., Spirito, S.: Quasiconvex elastodynamics: Weak-strong uniqueness for measure-valued solutions. Commun. Pure Appl. Math. 72, 1288–1320 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  28. Kružík, M., Roubíček, T.: Mathematical Methods in Continuum Mechanics of Solids. Springer, Switzerland (2019)

    Book  MATH  Google Scholar 

  29. Lattanzio, C., Tzavaras, A.E.: Structural properties of stress relaxation and convergence from viscoelasticity to polyconvex elastodynamics. Arch. Rational Mech. Anal. 180, 449–492 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  30. Lei, Z., Liu, C., Zhou, Y.: Global existence for a 2D incompressible viscoelastic model with small strain. Commun. Math. Sci. 5, 595–616 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  31. Lin, F.-H., Liu, C., Zhang, P.: On hydrodynamics of viscoelastic fluids. Commun. Pure Appl. Math. 58, 1437–1471 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  32. Liu, C., Walkington, N.J.: An Eulerian description of fluids containing visco-elastic particles. Arch. Rational Mech. Anal. 159, 229–252 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  33. Martinec, Z.: Principles of Continuum Mechanics. Birkhäuser/Springer, Switzerland (2019)

    Book  MATH  Google Scholar 

  34. Mielke, A., Roubíček, T.: Rate-independent elastoplasticity at finite strains and its numerical approximation. Math. Models Methods Appl. Sci. 6, 2203–2236 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  35. Mielke, A., Roubíček, T.: Thermoviscoelasticity in Kelvin–Voigt rheology at large strains. Arch. Rational Mech. Anal. 238, 1–45 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  36. Mindlin, R.D.: Micro-structure in linear elasticity. Arch. Rational Mech. Anal. 16, 51–78 (1964)

    Article  MathSciNet  MATH  Google Scholar 

  37. Nečas, J., Novotný, A., Šilhavý, M.: Global solution to the ideal compressible heat conductive multipolar fluid. Comment. Math. Univ. Carolinae 30, 551–564 (1989)

    MathSciNet  MATH  Google Scholar 

  38. Nečas, J., Ružička, M.: Global solution to the incompressible viscous-multipolar material problem. J. Elasticity 29, 175–202 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  39. Öttinger, H.C., Struchtrup, H., Liu, M.: Inconsistency of a dissipative contribution to the mass flux in hydrodynamics. Phys. Rev. E, 80, Art.no. 056303 (2009)

  40. Podio-Guidugli, P., Vianello, M.: Hypertractions and hyperstresses convey the same mechanical information. Contin. Mech. Thermodynam. 22, 163–176 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  41. Ružička, M.: Mathematical and physical theory of multipolar viscoelasticity. Bonner Mathematische Schriften 233, Bonn (1992)

  42. Rieger, M.O.: Young measure solutions for nonconvex elastodynamics. SIAM J. Math. Anal. 34, 1380–1398 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  43. Roubíček, T.: Quasistatic hypoplasticity at large strains Eulerian. J. Nonlinear Sci. to appear. Preprint arXiv no.2108.12718, (2021)

  44. Roubíček, T.: Nonlinear Partial Differential Equations with Applications, 2nd edn. Birkhäuser, Basel (2013)

    Book  MATH  Google Scholar 

  45. Roubíček, T.: Relaxation in Optimization Theory and Variational Calculus, 2nd edn. W. de Gruyter, Berlin (2020)

    Book  MATH  Google Scholar 

  46. Roubíček, T.: From quasi-incompressible to semi-compressible fluids. Discrete Contin. Dynam. Syst. 14, 4069–4092 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  47. Sideris, T.C., Thomases, B.: Global existence for three-dimensional incompressible isotropic elastodynamics via the incompressible limit. Commun. Pure Appl. Math. 58, 750–788 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  48. Temam, R.: Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (I). Arch. Rational Mech. Anal. 32, 135–153 (1969)

    Article  MathSciNet  MATH  Google Scholar 

  49. Tomassetti, G.: An interpretation of Temam’s stabilization term in the quasi-incompressible Navier-Stokes system. Applications in Engr. Sci., 5, Art.no. 100028 (2021)

  50. Toupin, R.A.: Elastic materials with couple stresses. Arch. Rational Mech. Anal. 11, 385–414 (1962)

    Article  MathSciNet  MATH  Google Scholar 

  51. Ván, P., Pavelka, M., Grmela, M.: Extra mass flux in fluid mechanics. J. Non-Equilib. Thermodyn. 42, 133–152 (2017)

    Article  Google Scholar 

  52. Šilhavý, M.: Multipolar viscoelastic materials and the symmetry of the coefficient of viscosity. Appl. Math. 37, 383–400 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  53. Wagner, D.H.: Symmetric-hyperbolic equations of motion for a hyperelastic material. J. Hyperbolic Differ. Equ. 6, 615–630 (2009)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The author is thankful to Ulisse Stefanelli and Giuseppe Tomassetti for valuable discussions about the Eulerian continuum mechanics, as well as to two anonymous referees for very careful reading of the original manuscript and many valuable comments.

Author information

Authors and Affiliations

  1. Mathematical Institute, Charles University, Sokolovská 83, CZ-186 75 Praha 8, Czech Republic

    Tomáš Roubíček

  2. Institute of Thermomechanics of the Czech Academy of Sciences, Dolejškova 5, CZ-182 00 Praha 8, Czech Republic

    Tomáš Roubíček

Authors
  1. Tomáš Roubíček
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tomáš Roubíček.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

This research was partially supported also from the MŠMT ČR (Ministry of Education of the Czech Republic) project CZ.02.1.01/0.0/0.0/15-003/0000493 and the institutional support RVO: 61388998 (ČR)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Roubíček, T. Visco-elastodynamics at large strains Eulerian. Z. Angew. Math. Phys. 73, 80 (2022). https://doi.org/10.1007/s00033-022-01686-z

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • DOI: https://doi.org/10.1007/s00033-022-01686-z

Keywords

Mathematics Subject Classification

Search

Navigation