Abstract
In this paper we derive a market-consistent value for long-term insurance contracts, with a focus on long-term health insurance contracts as found, e.g., in the German private health insurance industry. To this end, we first set up a health insurance company model and, second, conduct a simulation study to calculate the present value of future profits and the time value of financial options and guarantees from a portfolio of private health insurance policies. Our analysis quantifies the impact of investment results and underwriting surpluses on shareholder profits with respect to profit sharing rules and premium adjustment mechanisms. In contrast to the valuation of life insurance contracts with similar calculation techniques the results indicate that the time value of financial options and guarantees of German private health insurance contracts is substantially smaller in typical parameter settings.






Similar content being viewed by others
Notes
The outpatient health care expenditure data were obtained from the information system of the German federal health monitoring. http://www.gbe-bund.de.
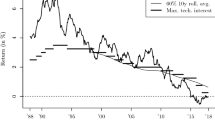
Note that in this illustration no adjustment is made for the aging portfolio of private health insurance companies (data not available). This adjustment would shift the upper curve downward.
More details on the stochastic processes are presented in the "Appendix".
We do not use the observed term structure of interest rates for the interest rate in the certainty equivalent scenario. Our definition provides us with a consistent certainty equivalent scenario; i.e., the computation of the inflation and interest development in the certainty equivalent scenario is identical.
Each scenario is a realization of \(\widetilde{\text {PVFP}}\); thus, we are considering an iid sequence of integrable random variables.
The development of the mortality rates may initiate an adjustment in practice as well. However, in general premium adjustments were initiated by the claim development (even if in recent years significant improvements in life expectancy could be observed). Thus, we neglect the mortality as an initiating factor here.
In the following we will cite sections from the insurance supervision act (VAG), the insurance contract act (VVG), calculation act (KalV), capital adequacy act (KapAusstV), surplus act (ÜbschV), and corporate tax act (KStG).
We do not distinguish between a “Rückstellung für erfolgsabhängige Beitragsrückerstattung” and a “Rückstellung fur erfolgsunabhängige Beitragsrückerstattung”.
Other assumptions on the relationship between premium and claim development are conceivable; they should be consistent with experience from the portfolio under consideration.
Policyholder behavior in private health insurance depends on many factors; especially the individual health condition, alternative tariffs within the insurance company as well as alternatives in the private health insurance market most likely influence the lapse decision.
This factorization is motivated by the historical observation that the scaling factor is to a large extent time-independent.
The superscript \(i\) always indicates that the value corresponds to an individual policyholder.
In practice, the extrapolation is proceeded during the previous period when \(C_{k-1}^{*}\) is unknown. We adopt this approach. In addition, this is in line with regulatory requirements (§ 14 KalV). Our approach is still a simplification as for instance the verification of an independent trustee is not considered. There are different approaches allowed to extrapolate average claim per capita.
§ 203 VVG. By § 12b (2) VAG, it is \(\varepsilon \le 0.10\).
We do not model the fact that the maximal time period for capital in the surplus funds is three years due to tax reasons (§ 21 KStG) and we neglect special rules for policyholders aged 80+.
If the full additional reserve is required to curb the premium, the full additional reserve is shifted to the actuarial reserve. Additional management rules may be applied in this process.
All calculations are performed with the software R [27].
References
Allianz Group (2012) Market consistent embedded value report 2011. https://www.allianz.com/media/investor_relations/en/results_reports/annual_report/ar2011/evr2011.pdf. Accessed 2 Aug 2012
Bacinello A (2003) Pricing guaranteed life insurance participating policies with annual premiums and surrender option. N Am Actuar J 7(3):1–17
Balestreri A, Kent J, Morgan E (2011) Dynamic asset liability management: a method for optimising investment strategy. Eur Actuar J 1:29–46
Brigo D, Mercurio F (2006) Interest rate models: theory and practice: with smile, inflation, and credit. Springer, Berlin
Buchner F, Wasem J (2006) Steeping of health expenditure profiles. Geneva Papers 31(4):581–599
Castellani G, De Felice M, Moriconi F, Pacati C (2005) Embedded value in life insurance. http://www.econ-pol.unisi.it/didattica/imaav/EVLI.pdf. Accessed 2 Aug 2012
CFO Forum (2009) Market consistent embedded value basis for conclusions. http://www.cfoforum.eu/downloads/CFO_Forum_MCEV_Basis_for_Conclusions.pdf. Accessed 2 Aug 2012
CFO Forum (2009) Market consistent embedded value principles. http://www.cfoforum.eu/downloads/MCEV_Principles_and_Guidance_October_2009.pdf. Accessed 2 Aug 2012
Cipollini A, Canty P (2010) Inflation breakeven in the Jarrow and Yildirim model and resulting pricing formulas. Quant Finance 1–22: doi:10.1080/14697688.2010.503711
Coppola M, Di Lorenzo E, Orlando A, Sibillo M (2011) Solvency analysis and demographic risk measures. J Risk Finance 12(4):252–269
Diers D, Eling M, Kraus C, Reuß A (2012) Market-consistent embedded value in non-life insurance: how to measure it and why. J Risk Finance 13:250–275
Dodgson M, Kainth D (2006) Inflation-linked derivatives. Royal Bank of Scotland Risk Training Course, Market Risk Group
Doherty NA, Garven JR (1986) Price regulation in property-liability insurance: a contingent-claims approach. J Finance 41(5):1031–1050
Drees H, Milbrodt H (1995) Möglichkeiten zur Milderung der Beitragssteigerung bei älteren Versicherten in der deutschen privaten Krankenversicherung—eine Simulationsstudie. Blätter der DGVFM 22(2):393–418
Drees H, Maas B, Milbrodt H (1996) Möglichkeiten zur Milderung der Beitragssteigerung bei älteren Versicherten in der deutschen privaten Krankenversicherung II. Blätter der DGVFM 22(3):581–590
Frasca R, LaSorella K (2009) Embedded value: practice and theory. Actuarial Practice Forum
Gatzert N, Schmeiser H (2008) Combining fair pricing and capital requirements for non-life insurance companies. J Bank Finance 32(12):2589–2596
Gerstner T, Griebel M, Holtz M, Goschnick R, Haep M (2008) A General asset-liability management model for the efficient simulation of portfolios of life insurance policies. Insur Math Econ 42(2):704–716
Grosen A, Jørgensen P (2002) Life insurance liabilities at market value: an analysis of insolvency risk, bonus policy, and regulatory intervention rules in a barrier option framework. J Risk Insur 69(1):63–91
Jarrow R, Yildirim Y (2003) Pricing treasury inflation protected securities and related derivatives using an HJM model. J Financ Quant Anal 38(2):337–358
Kling A, Richter A, Ruß J (2007) The interaction of guarantees, surplus distribution, and asset allocation in with-profit life insurance policies. Insur Math Econ 40(1):164–178
Kochanski M, Karnarski B (2011) Solvency capital requirement for hybrid products. Eur Actuar J 1:173–198
Maiwald KJ, Schulze S, Weber R (2004) Der aktuarielle Unternehmenszins: ein Instrument zur unternehmensindividuellen Festlegung des Rechnungszinses in der privaten Krankenversicherung. Der Aktuar 10(4):122–125
Malamud S, Trubowitz E, Wüthrich M (2008) Market consistent pricing of insurance products. ASTIN Bull 38(2):483–526
Mehrotra A, Dudley R, Luft H (2003) What’s behind the health expenditure trends? Ann Rev Public Health 24(1):385–412
Newhouse J (1992) Medical care costs: how much welfare loss? J Econ Perspect 6(3):3–21
R Development Core Team (2011) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, http://www.R-project.org/. ISBN 3-900051-07-0
Schmidt JP (2012) Market Consistent Embedded Value in der privaten Krankenversicherung. Zeitschrift für die gesamte Versicherungswissenschaft 101(2):223–253
Schneider E (2002) The main features of the German private health insurance. 27th ICA Health Seminar, Cancun
Sheldon T, Smith A (2004) Market consistent valuation of life assurance business. Br Actuar J 10(3):543–605
Wolfsdorf K (1997) Versicherungsmathematik Teil 1 Personenversicherung. Teubner, Stuttgart
Wüthrich M, Furrer H, Bühlmann H (2010) Market-consistent actuarial valuation. Springer, Berlin
Acknowledgments
The author thanks Sandra Blome, Marcus C. Christiansen, Martin Eling, Joachim Pricking, Andreas Reuß, Ulrich Stellmann, Hans-Joachim Zwiesler, and two anonymous referees for very helpful comments and discussions on previous drafts and talks.
Author information
Authors and Affiliations
Corresponding author
Additional information
This work was financially supported by the ,,Wissenschaftsförderungsprogramm“ (Deutscher Verein für Versicherungswissenschaft e.V.).
Appendix: Remarks on the stochastic environment
Appendix: Remarks on the stochastic environment
In the following we give a short review of the JY-model. The review is similar to the description of the model in [4, 9, 12, 20].
Consider a financial market with finite horizon \(T\) described by the probability space \((\Omega ,\mathcal {F},P)\) and filtration \((\mathcal {F}_t)_{0\le t\le T}\). The probability measure \(P\) is the real-world measure. The model is based on the assumption that there exist nominal as well as real prices in the financial market. The inflation (i.e. the development of the consumer price index) explains the difference between the corresponding nominal and real economy. The JY-model is an analog to a two-currency interest rate model, whereas the inflation rate in the JY-model corresponds to the spot exchange rate in the two-currency analog.
The following two equations constitute a Heath-Jarrow-Morton framework for the instantaneous forward rates \(f_n(t,T)\) (nominal economy) and \(f_r(t,T)\) (real economy). The instantaneous forward rates under the real-world probability measure \(P\) satisfy the following stochastic differential equations for \(t\in [0,T]\):
with initial conditions \(f_n(0,T)=f_n^M(0,T)\) and \(f_r(0,T)=f_r^M(0,T)\). \(\alpha _n(t,T)\) and \(\alpha _r(t,T)\) are adapted processes; \(\varsigma _n(t,T)\) and \(\varsigma _r(t,T)\) are deterministic functions; \(W_n^P(t)\) and \(W_r^P(t)\) are Brownian Motions. \(f_n^M(0,T)\) and \(f_r^M(0,T)\) denote the observed instantaneous forward rates in the market at time 0 for maturity \(T\); i.e.,
\(P_n^M(0,T)\), \(P_r^M(0,T)\) are the bond prices in the nominal and real market for maturity \(T\).
The development of the consumer price index \(I(t)\) is explained in terms of a Geometric Brownian Motion, i.e.
with initial condition \(I(0)=I_0>0\), an adapted process \(\mu (t)\), and a positive constant volatility parameter \(\sigma _I\).
The three Brownian motions \(W_n^P(t)\), \(W_r^P(t)\), and \(W_I^P(t)\) are correlated with correlation coefficients \(\rho _{n,r}\), \(\rho _{n,I}\) and \(\rho _{r,I}\). It is
Following [20] we assume a decaying volatility structure. For \(t\in [0,T]\) we let
with positive constants \(a_n\), \(a_r\), \(\sigma _n\) and \(\sigma _r\).
A change of measure from the real-world measure \(P\) to the risk-neutral measure \(Q^n\) (corresponding to the nominal economy) and a restatement of the stochastic differential equations in terms of short rates yields
Again the three Brownian motions \(W_n\), \(W_r\), and \(W_I\) are correlated with the parameters \(\rho _{n,r}\), \(\rho _{n,I}\), and \(\rho _{r,I}\), and we have
to fit the observed term structure at the initial date. \(\frac{\partial f^M_n(0,t)}{\partial t}\) and \(\frac{\partial f^M_n(0,t)}{\partial t}\) denote the partial derivatives of \(f^M_n(0,t)\) and \(f^M_r(0,t)\) with respect to the second argument. The equations for the nominal and real interest rate under the risk-neutral measure \(Q^n\) are referred to in the literature as the “Hull-White Extended Vasicek” model [4]. Note that the drift term of the inflation process after the measure change is described by the difference of the nominal and real short rate. In economic literature, other authors denote this relation as the Fisher equation.
Rights and permissions
About this article
Cite this article
Schmidt, JP. Market-consistent valuation of long-term insurance contracts: valuation framework and application to German private health insurance. Eur. Actuar. J. 4, 125–153 (2014). https://doi.org/10.1007/s13385-014-0087-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13385-014-0087-y