Discrete Excitation Spectrum of a Classical Harmonic Oscillator in Zero-Point Radiation

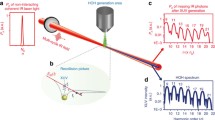
Abstract

We report that upon excitation by a single pulse, a classical harmonic oscillator immersed in the classical electromagnetic zero-point radiation exhibits a discrete harmonic spectrum in agreement with that of its quantum counterpart. This result is interesting in view of the fact that the vacuum field is needed in the classical calculation to obtain the agreement.

Appendices

The Derivation of $\langle W_{1\omega _{0}} \rangle$

In this appendix, the value of $\langle W_{1\omega _{0}} \rangle$ is calculated. This expounds the steps leading from Eq. (36) to Eq. (37). We will focus here on $\langle W_{1\omega _{0}} \rangle$ and indicate how the steps are different in notation for $\langle W_{2\omega _{0}} \rangle$ and $\langle W_{3\omega _{0}} \rangle$. In Eq. (36), the energy change at drive frequency $\omega _{p} \simeq 1\omega _{0}$ is

$$\begin{aligned} W_{1\omega _{0}} = \frac{\sqrt{\pi }}{2} (D_{0} \omega _{0})(qE_{0}\Delta t) \times \exp {\left[ - \left( \frac{\omega _{p} - \omega _{0}}{2/\Delta t} \right) ^2 \right] } \cos {(\omega _{0}t_{c} + \varphi _{0})}. \end{aligned}$$

(39)

The initial conditions come in by substituting $D_{0}$ and $\varphi _{0}$, using

$$\begin{aligned} \cos {(\varphi _{0})}&= (x_{0}-x_{1p}(0))/D_{0}, \nonumber \\ \sin {(\varphi _{0})}&= -(v_{0}-v_{1p}(0))/D_{0}\omega _{0}, \end{aligned}$$

(40)

as defined in Eq. (26), and expanding $\cos {(\omega _{0}t_{c} + \varphi _{0})}$ to $\cos {(\omega _{0}t_{c})}\cos {(\varphi _{0})}-\sin {(\omega _{0}t_{c})}\sin {(\varphi _{0})}$ so that

$$\begin{aligned} D_{0}\cos {(\omega _{0}t_{c} + \varphi _{0})} = \cos {(\omega _{0}t_{c})}(x_{0}-x_{1p}(0)) + \sin {(\omega _{0}t_{c})}(v_{0}-v_{1p}(0))/\omega _{0}. \end{aligned}$$

(41)

The energy change $W_{1\omega _{0}}$ now depends on $x_{0}$, $v_{0}$, $x_{1p}(0)$, and $v_{1p}(0)$. Similar procedure is also used to evaluate $\langle W_{2\omega _{0}} \rangle$ and $\langle W_{3\omega _{0}}\rangle$, where the sinusoidal functions are expanded and substitutions are made using Eqs. (30) and (34),

$$\begin{aligned}&\cos {(\phi _{0})} = x_{0}/A_{0}, \nonumber \\&\sin {(\phi _{0})} = -v_{0}/A_{0}\omega _{0}, \nonumber \\&\cos {(\xi _{0})} = -{x_{2p}^{(1)}(0)}/B_{0}, \nonumber \\&\sin {(\xi _{0})} = {v_{2p}^{(1)}(0)}/B_{0}\omega _{0}, \nonumber \\&\cos {(\zeta _{0})} = -{x_{3p}^{(1)}(0)}/C_{0}, \nonumber \\&\sin {(\zeta _{0})} = {v_{3p}^{(1)}(0)}/C_{0}\omega _{0}. \end{aligned}$$

(42)

To compute the ensemble average of Eq. (39), the values of $\langle x_{0}\rangle$, $\langle v_{0}\rangle$, $\langle x_{1p}(0) \rangle$, and $\langle v_{1p}(0) \rangle$ are needed. The statistical moments, $\langle x_{0}\rangle$ and $\langle v_{0}\rangle$, can be evaluated given the stationary state of the harmonic oscillator in the vacuum field [2],

$$\begin{aligned} \langle x_{0}\rangle = 0, \quad \langle v_{0}\rangle = 0. \end{aligned}$$

(43)

As the particular solution ($x_{1p}(0)$ and $v_{1p}(0)$) does not depend on $x_{0}$ or $v_{0}$, its ensemble average is equal to itself,

$$\begin{aligned} \langle x_{1p}(0) \rangle = x_{1p}(0), \nonumber \\ \langle v_{1p}(0) \rangle = v_{1p}(0). \end{aligned}$$

(44)

The particular solutions are evaluated at $t=0$ according to Eq. (25),

$$\begin{aligned} x_{1p}(0)&= -\int _{0}^{\infty } \!d\omega f_{1}(\omega ) \sin {(-\omega t_{c})}, \nonumber \\ v_{1p}(0)&= -\int _{0}^{\infty } \!d\omega f_{1}(\omega ) \omega \cos {(-\omega t_{c})}, \end{aligned}$$

(45)

where

$$\begin{aligned} f_{1}(\omega ) \equiv \frac{\Delta t}{2\sqrt{\pi }} \frac{qE_{0}}{m(\omega _{0}^2-\omega ^2)} \exp { \left[ -\left( \frac{\omega -\omega _{p}}{2/\Delta t}\right) ^2 \right] }. \end{aligned}$$

(46)

Using the change of variables, $u \equiv \omega /\omega _{0}$, $u_{p} \equiv \omega _{p}/\omega _{0}$, $\Delta u \equiv 2/\omega _{0}\Delta t$, and $\kappa \equiv \omega _{0}t_{c}$, the particular solutions in Eq. (45) can be written as

$$\begin{aligned} x_{1p}(0)&= \left( \frac{qE_{0}\Delta t}{m\omega _{0}}\frac{1}{2\sqrt{\pi }} \right) D_{1}, \nonumber \\ v_{1p}(0)&= \left( \frac{-qE_{0}\Delta t}{m}\frac{1}{2\sqrt{\pi }} \right) D_{2}, \end{aligned}$$

(47)

where

$$\begin{aligned} D_{1}&\equiv \int _{0}^{\infty } \!du \frac{1}{1-u^{2}} \exp { \left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \sin {(\kappa u)}, \nonumber \\ D_{2}&\equiv \int _{0}^{\infty } \!du \frac{u}{1-u^{2}} \exp { \left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \cos {(\kappa u)}. \end{aligned}$$

(48)

Therefore, the ensemble average of Eq. (39) is

$$\begin{aligned} \langle W_{1\omega _{0}} \rangle&= \frac{\sqrt{\pi }}{2} \omega _{0}(qE_{0}\Delta t) \exp {\left[ - \left( \frac{\omega _{p} - \omega _{0}}{2/\Delta t} \right) ^2 \right] } \langle D_{0}\cos {(\omega _{0}t_{c} + \varphi _{0})} \rangle \nonumber \\&= \frac{-1}{4} \frac{(qE_{0}\Delta t)^{2}}{m} \exp {\left[ - \left( \frac{\omega _{p} - \omega _{0}}{2/\Delta t} \right) ^2 \right] } \left( D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )} \right) .\qquad \quad \end{aligned}$$

(49)

The integral $D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )}$ can be further evaluated,

$$\begin{aligned}&D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )} \nonumber \\&= \int _{0}^{\infty } \!du \frac{1}{1-u^{2}} \exp { \left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \left( \sin {(\kappa u)}\cos {(\kappa )} - u\cos {(\kappa u)}\sin {(\kappa )} \right) \nonumber \\&= \int _{0}^{\infty } \!du \frac{1}{2(1+u)} \exp { \left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \sin {(\kappa (u+1))} \nonumber \\&\quad +\,\int _{0}^{\infty } \!du \frac{1}{2(1-u)} \exp {\left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \sin {(\kappa (u-1))}. \end{aligned}$$

(50)

Because $u_{p} \simeq 1$, the first term

$$\begin{aligned} \int _{0}^{\infty } \!du \frac{1}{2(1+u)} \exp { \left[ -\left( \frac{u-u_{p}}{\Delta u}\right) ^2 \right] } \sin {(\kappa (u+1))} \end{aligned}$$

(51)

is effectively zero. Let $u_{p} = 1-\epsilon \Delta u$, where $\epsilon \ll 1$ is a small number, we obtain

$$\begin{aligned} D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )} = \frac{-1}{2}\int _{0}^{\infty } \!du \frac{\sin {(\kappa (u-1))}}{u-1} \exp { \left[ -\left( \frac{u-1}{\Delta u} + \epsilon \right) ^2 \right] }. \end{aligned}$$

(52)

By the change of variables $x \equiv (u-1)/\Delta u$ and $\alpha \equiv \kappa \Delta u$, the above integral can be rewritten as

$$\begin{aligned} \int _{0}^{\infty } \!du \frac{\sin {(\kappa (u\!-\!1))}}{u\!-\!1} \exp { \left[ \!-\!\left( \frac{u\!-\!1}{\Delta u} \!+\! \epsilon \right) ^2 \right] } = \int _{-1/\Delta u}^{\infty } \! dx \frac{\sin {(\alpha x)}}{x} \exp { \left[ -\left( x \!+\! \epsilon \right) ^2 \right] }. \end{aligned}$$

(53)

Because the width of the integrand is much smaller than the lower integral limit, $\pi /\alpha \ll 1/\Delta u$, the integral can be approximated by extending the lower limit to the negative infinity,

$$\begin{aligned} \int _{-1/\Delta u}^{\infty } \! dx \frac{\sin {(\alpha x)}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] } \simeq \int _{-\infty }^{+\infty } \!\! dx \frac{\sin {(\alpha x)}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] }, \end{aligned}$$

(54)

which can be written in the complex form,

$$\begin{aligned} \int _{-\infty }^{+\infty } \!\! dx \frac{\sin {(\alpha x)}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] } = \mathrm Im \left( \int _{-\infty }^{+\infty } \!\! dx \frac{e^{i\alpha x}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] } \right) . \end{aligned}$$

(55)

We will use the contour integral to evaluate this complex integral,

$$\begin{aligned} \oint _{C} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] }&= \int _{C_{S}} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } \nonumber \\&\quad +\,\int _{C_{L}} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z\,+\,\epsilon \right| ^2 \right] } \nonumber \\&\quad +\,\int _{-\infty }^{+\infty } \!\! dx \frac{e^{i\alpha x}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] }. \end{aligned}$$

(56)

The contour $C$ consists of one large hemicircles $C_{L}$ on the upper-half of the complex plane, one small hemicircle $C_{S}$ on the lower-half complex plane around the pole $z=0$, and a line on the real axis from the negative infinity to the positive infinity. The integral along $C_{L}$ is zero according to Jordan’s lemma,

$$\begin{aligned} \int _{C_{L}} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } = 0. \end{aligned}$$

(57)

The integral along $C_{S}$ can be evaluated as

$$\begin{aligned} \int _{C_{S}} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } = \pi i \left( e^{i\alpha z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } \right) \Big |_{z=0} = \pi i e^{-\epsilon ^2}. \end{aligned}$$

(58)

The contour integral is evaluated accordingly to the Cauchy integral formula,

$$\begin{aligned} \oint _{C} \! dz \frac{e^{i\alpha z}}{z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } = 2 \pi i \left( e^{i\alpha z} \exp { \left[ -\left| z + \epsilon \right| ^2 \right] } \right) \Big |_{z=0} = 2 \pi i e^{-\epsilon ^2}. \end{aligned}$$

(59)

Therefore, we obtain for values of $\alpha \gg 1$ the value of the integral in Eq. (55),

$$\begin{aligned} \int _{-\infty }^{+\infty } \!\! dx \frac{\sin {(\alpha x)}}{x} \exp { \left[ -\left( x + \epsilon \right) ^2 \right] } = \mathrm Im \left( \pi i e^{-\epsilon ^2} \right) = \pi e^{-\epsilon ^2}. \end{aligned}$$

(60)

Combining Eqs. (52),  (53), (54), and (55), the integral $D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )}$ in Eq. (49) can be evaluated,

$$\begin{aligned} D_{1}\cos {(\kappa )} - D_{2}\sin {(\kappa )} = \frac{-\pi }{2} \exp { \left[ -\left( \frac{\omega _{p}-\omega _{0}}{2/\Delta t}\right) ^2 \right] }. \end{aligned}$$

(61)

Given Eqs. (49) and (61), the ensemble average of the energy change at drive frequency $\omega _{p} \simeq 1\omega _{0}$ is

$$\begin{aligned} \langle W_{1\omega _{0}} \rangle = \frac{\pi }{8}\frac{(qE_{0}\Delta t)^2}{m}\exp {\left[ - 2\left( \frac{\omega _{p} - \omega _{0}}{2/\Delta t} \right) ^2 \right] }. \end{aligned}$$

(62)

Quantum Perturbation Analysis

In this appendix, we use the second-order quantum perturbation to obtain the energy expectation value for an harmonic oscillator that is excited by a propagating Gaussian pulse. The Gaussian pulse is calculated beyond dipole approximation. In other words, the pulse field has spatial dependence in addition to its temporal dependence. The agreement between quantum perturbation analysis and quantum simulation is about $80~\%$. The result of the quantum analysis is similar to that of the classical analysis given in Eq. (37). A brief summary for the derivation of the quantum analysis is given in the following. The quantum state of an harmonic oscillator is

$$\begin{aligned} |\psi \rangle (t) = \sum _{n=0}^{\infty } c_{n}(t)e^{-i\omega _{n}t}|n\rangle , \end{aligned}$$

(63)

where $|n\rangle$ is the unperturbed eigenstate, $\omega _{n} = \omega _{0}(n+1/2)$ is the eigenfrequency, and $c_{n}(t)$ is the probability amplitude. In the interaction picture, the Schrödinger equation with the unperturbed Hamiltonian $\widehat{H}_{0}$ and the perturbative Hamiltonian $\widehat{H}^{'}$ can be generally written as

$$\begin{aligned} i\hbar \frac{d}{dt}\left( \sum _{n=0}^{\infty } c_{n}(t)|n\rangle \right) = \widehat{\fancyscript{H}} \left( \sum _{n=0}^{\infty } c_{m}(t)|m\rangle \right) , \end{aligned}$$

(64)

where $\displaystyle {\widehat{\fancyscript{H}} = e^{\frac{i}{\hbar } \widehat{H}_{0} t} \widehat{H}^{'} e^{-\frac{i}{\hbar } \widehat{H}_{0} t} }$. Using the second-order perturbation theory, the perturbative expansion of the probability amplitude $c_{n}(t) \simeq c_{n}^{(0)}(t) + \lambda _{n} c_{n}^{(1)}(t) + \lambda ^{2}_{n} c_{n}^{(2)}(t)$ turns the Schrödinger equation into a system of equations,

$$\begin{aligned} \left\{ \begin{array}{ll} i\hbar \frac{d}{dt}\left( \sum _{n=0}^{\infty } c^{(0)}_{n}(t)|n\rangle \right) &{}= 0 \\ i\hbar \frac{d}{dt}\left( \sum _{n=0}^{\infty } \lambda _{n}c^{(1)}_{n}(t)|n\rangle \right) &{}= \widehat{H}^{'} \left( \sum _{n=0}^{\infty } c^{(0)}_{m}(t)|m\rangle \right) \\ i\hbar \frac{d}{dt}\left( \sum _{n=0}^{\infty } \lambda ^{2}_{n}c^{(2)}_{n}(t)|n\rangle \right) &{}= \widehat{H}^{'} \left( \sum _{n=0}^{\infty } \lambda _{n}c^{(1)}_{m}(t)|m\rangle \right) , \end{array} \right. \end{aligned}$$

(65)

where $\lambda _{n}$ denotes the expansion factor for $c_{n}(t)$. In our study, the perturbative Hamiltonian $\widehat{H}^{'}$ is provided by the interaction between a charged quantum particle and a classical field,

$$\begin{aligned} \widehat{H}^{'} = -\frac{q}{2m}\left( 2\mathbf {A}_{p}\cdot \hat{\mathbf {p}}- q\mathbf {A}_{p}^2 \right) ,\end{aligned}$$

(66)

where $q$ and $m$ are the charge and the mass of the particle. The driving field $\mathbf {A}_{p}$ is a propagating Gaussian pulse,

$$\begin{aligned} \mathbf {A}_{p}= A_{p} \cos {( \mathbf {k}_{p}\cdot \hat{\mathbf {x}}- \omega _{p} \tau )} \exp {\left[ - \left( \frac{\mathbf {k}_{p}\cdot \hat{\mathbf {x}}}{|\mathbf {k}_{p}|\Delta x} - \frac{\tau }{\Delta t} \right) ^2 \right] }\varvec{\varepsilon }_{p}, \end{aligned}$$

(67)

where $\tau = t - t_{c}$, $\mathbf {k}_{p} = \omega _{p}/c\left( \sin {\theta _{p}}, 0, \cos {\theta _{p}} \right)$ is the wave vector of the field and $\varvec{\varepsilon }_{p}= \left( \cos {\theta _{p}}, 0, -\sin {\theta _{p}} \right)$ is the field polarization. Note that in order to take the calculation beyond the dipole approximation, we will keep the operator $\hat{\mathbf {x}}$ in the function form of the driving field $\mathbf {A}_{p}$. Using $\mathbf {k}_{p}\cdot \hat{\mathbf {x}}$ as an expansion factor for $\mathbf {A}_{p}$, the perturbative Hamiltonian can be expanded. In the interaction picture, the expanded perturbative Hamiltonian is

$$\begin{aligned} \widehat{\fancyscript{H}} \simeq \widehat{\fancyscript{H}}_{1\omega _{0}}(t) + \widehat{\fancyscript{H}}_{2\omega _{0}}(t) + \widehat{\fancyscript{H}}_{3\omega _{0}}(t), \end{aligned}$$

(68)

where

$$\begin{aligned} \widehat{\fancyscript{H}}_{1\omega _{0}}(t)&= f_{1}(t) \left( \hat{b}^{\dagger }e^{i\omega _{0}t} - \hat{b}e^{-i\omega _{0}t} \right) , \nonumber \\ \widehat{\fancyscript{H}}_{2\omega _{0}}(t)&= f_{2}(t) \left( \hat{b}^{\dagger 2}e^{i2\omega _{0}t} + \hat{1\!\!1} - \hat{b}^{2}e^{-i2\omega _{0}t} \right) , \nonumber \\ \widehat{\fancyscript{H}}_{3\omega _{0}}(t)&= f_{3}(t) \left[ \hat{b}^{\dagger 3}e^{i3\omega _{0}t} + \left( \hat{b}\hat{b}^{\dagger 2}e^{i\omega _{0}t} - \hat{b}^{\dagger }\hat{b}^{2}e^{-i\omega _{0}t} \right) \right. \nonumber \\&\left. + \left( \hat{b}^{\dagger }e^{i\omega _{0}t} + \hat{b}e^{-i\omega _{0}t} \right) - \hat{b}^{3}e^{-i3\omega _{0}t} \right] + g_{3}(t) \hat{1\!\!1}. \end{aligned}$$

(69)

The symbol $\hat{b}^{\dagger }$ and $\hat{b}$ are the raising and the lowing operators for the harmonic oscillator. The symbol $\hat{1\!\!1}$ denotes the identity operator.

The time-dependent functions $f_{1}(t)$, $f_{2}(t)$, $f_{3}(t)$, and $g_{3}(t)$ are defined as

$$\begin{aligned} f_{1}(t)&= \left[ \left( \frac{-qA_{p}\varepsilon _{x}}{m} \right) i \sqrt{\frac{\hbar m \omega _{0}}{2}} \right] \cos {( \omega _{p} \tau )}\exp {(- \tau ^{2}/\Delta t^{2})}, \nonumber \\ f_{2}(t)&= \left[ \left( \frac{-qA_{p}\varepsilon _{x}}{m} \right) k_{x} \sqrt{\frac{\hbar }{2 m \omega _{0}}} i \sqrt{\frac{\hbar m \omega _{0}}{2}}\right] \sin {( \omega _{p} \tau )}\exp {(- \tau ^{2}/\Delta t^{2})} , \nonumber \\ f_{3}(t)&= \left[ \left( \frac{qA_{p}\varepsilon _{x}}{m} \right) \frac{k^{2}_{x}}{2} \left( \sqrt{\frac{\hbar }{2 m \omega _{0}}} \right) ^{2} i \sqrt{\frac{\hbar m \omega _{0}}{2}}\right] \cos {( \omega _{p} \tau )}\exp {(- \tau ^{2}/\Delta t^{2})}, \nonumber \\ g_{3}(t)&= \left( \frac{-q^{2}A^2_{p}}{m} \right) \cos ^{2}{( \omega _{p} \tau )}\exp {(- \tau ^{2}/\Delta t^{2})}. \end{aligned}$$

(70)

In the case of $1\omega _{0}$-excitation with $\omega _{p} \simeq 1\omega _{0}$, only the $\widehat{\fancyscript{H}}_{1\omega _{0}}(t)$ term is effective. In the cases of $2\omega _{0}$-excitation with $\omega _{p} \simeq 2\omega _{0}$, only the $\widehat{\fancyscript{H}}_{2\omega _{0}}(t)$ term is effective. In the case of $3\omega _{0}$-excitation with $\omega _{p} \simeq 3\omega _{0}$, only the $\widehat{\fancyscript{H}}_{3\omega _{0}}(t)$ term is effective. Assuming that the harmonic oscillator is initially at the ground state, the expectation value of the energy change can be calculated up to $\lambda ^{2}_{n}$,

$$\begin{aligned} \langle \Delta E_{1\omega _{0}} \rangle&= \frac{\pi }{8}\left( \frac{q^{2}A^{2}_{p}\omega _{0}^{2}\Delta t^{2}}{m} \right) \exp {\left[ -2\left( \frac{\omega _{p} - \omega _{0}}{2/\Delta t} \right) ^{2} \right] } \cos ^2{(\theta _{p})} , \nonumber \\ \langle \Delta E_{2\omega _{0}} \rangle&= \frac{\pi }{16}\left( \frac{4q^{2}A^{2}_{p}\omega _{0}^{2}\Delta t^{2}}{m} \right) \left( \frac{\hbar \omega _{p}}{mc^{2}} \right) \left( \frac{\omega _{p}}{\omega _{0}}\right) \sin ^2{(\theta _{p})} \nonumber \\&\times \exp {\left[ -2\left( \frac{\omega _{p} - 2\omega _{0}}{2/\Delta t} \right) ^{2} \right] } \cos ^2{(\theta _{p})}, \nonumber \\ \langle \Delta E_{3\omega _{0}} \rangle&= \frac{3\pi }{16^2}\left( \frac{12q^{2}A^{2}_{p}\omega _{0}^{2}\Delta t^{2}}{m} \right) \left[ \left( \frac{\hbar \omega _{p}}{mc^{2}} \right) \left( \frac{\omega _{p}}{\omega _{0}}\right) \sin ^2{(\theta _{p})} \right] ^{2} \nonumber \\&\times \exp {\left[ -2\left( \frac{\omega _{p} - 3\omega _{0}}{2/\Delta t} \right) ^{2} \right] } \cos ^2{(\theta _{p})}. \end{aligned}$$

(71)

The result of quantum perturbation analysis, Eq. (71), is compared with quantum simulation in Fig. 3. The agreement is about $80~\%$. In the same figure, the quantum analysis is also compared with the classical analysis, Eq. (37). The quantum analysis agrees well with the classical analysis, as evidenced by the similarity between Eqs. (71) and (37).

Fig. 3

Comparison between quantum analysis, quantum simulation, and classical analysis. Up the overall agreement between quantum perturbation and quantum simulation is within $80~\%$. Bottom the quantum analysis and the classical analysis shows identical resonance structures at $\omega _{p} \simeq 1\omega _{0}$ and $\omega _{p} \simeq 2\omega _{0}$, while the agreement at $\omega _{p} \simeq 3\omega _{0}$ is about $65~\%$