Skip to main content
SpringerLink
Log in

Determination of optimum aspect ratio for laminar flow heat transfer of dilute viscoelastic solutions in flattened tube heat exchangers

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

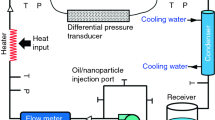
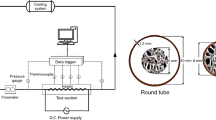
Heat transfer of viscoelastic liquids in five flattened tubes with aspect ratios ranging from 1.4 to 5.7 were presented. Water was used as the heating medium; and solutions of polyacrylamide were used as the viscoelastic solutions. Heat transfer increase from flattening was 101% higher while secondary flow contributed a maximum increase of 65% for the 250 ppm solution and about 85% for the 500 ppm solutions at an aspect ratio of 1.6.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

Abbreviations

a:

Major axis

A:

Area

b:

Minor axis

c:

Straight section of the flattened tube cross-section = a−b

cp :

Specific heat

C:

Constant

d:

Original tube diameter

de :

Equivalent diameter

dc :

Characteristic dimension

F, G, H:

Shear rate functions

F0, G0, H0 :

Shear rate functions coefficients

Gz:

Greatz number

Gze :

Graetz number using equivalent diameter

hc :

Heat transfer coefficient, circular tube

hf :

Heat transfer coefficient, flattened tube

k:

Thermal conductivity

K:

Material constant

K’:

Constant in Graetz–Leveque equation

L:

Length

Nu:

Nusselt number

Nue :

Nusselt number using equivalent diameter

Nul :

Local Nusselt number

p:

Aspect ratio

P:

Pressure gradient

q:

Heat flux

qr :

Shear rate

Q:

Volumetric flow rate

Q1 :

Flow rate for central region, flattened tube

Q2 :

Flow rate for semi-circular ends, flattened tube

R:

Radius

t:

Time

T:

Temperature

T1 :

Inlet temperature

T2 :

Outlet temperature

Tw :

Wall temperature

ΔTA :

Temperature difference between the two streams at entry

ΔTB :

Temperature difference between the two streams at exit

ΔTLM :

Log mean temperature difference

U:

Overall heat transfer coefficient

v:

Velocity

vmax :

Peak velocity

vs :

Secondary flow velocity

w:

Mass flow rate

W:

Watt

γ:

Strain

λ1 :

Relaxation time

λ2 :

Retardation time

ρ:

Density

τ:

Shear stress

μw, μb :

Viscosity at wall, bulk viscosity

Φ:

Geometric factor

References

  1. Bott TR (1966) Design of scraped surface heat exchangers. British Chem Eng 2(5):338–339

    Google Scholar 

  2. Bott TR (2001) To foul or not to foul. Chem Eng Prog Mag 97(11):30–37

    Google Scholar 

  3. Bott TR, Romero JJB (1963) Heat transfer across a scraped surface. Can J Chem Eng 41:213–219

    Article  Google Scholar 

  4. Chong A (2001) A study of scraped-surface heat exchanger in ice-making applications. M.Sc. Thesis. University of Toronto

  5. Tähti T (2004) Suspension melt crystallization in tubular and scraped surface heat Exchangers. Ph. D. Thesis. Martin-Luther-Universität

  6. Song L (2008) Vibration actuation system with independent control of frequency and amplitude. Free Patent on Line, Patent Application: 20100193159

  7. Nassauer L, Kessler HG (1986) The effect of electrostatic phenomena on the cleaning of surfaces. Chem Eng Process 20(1):43–52

    Article  Google Scholar 

  8. Pattenden RF, Richards AD (1964) Heat transfer from a rotating tube with controlled fluid flow. Arch J Mech Eng Sci 6:144–149

    Article  Google Scholar 

  9. Liu S, Masliyah JH (1994) Developing convective heat transfer in helical pipes with finite pitch. Int J Heat Fluid Flow 15(1):66–74

    Article  Google Scholar 

  10. Yang R, Chang CF (1994) Combined free and forced convection for developed flow in curved pipes with finite curvature ratio. Int J Heat Fluid Flow 15:470–476

    Article  Google Scholar 

  11. Green AE, Rivlin RS (1956) Steady flow of non-Newtonian fluids through tubes. Q Appl Math 14(1956):299–308

    MathSciNet  MATH  Google Scholar 

  12. Carlson LW, Irvine TF Jr (1961) Fully developed pressure drop in triangular shaped ducts. J Heat Transf 83:441–444

    Article  Google Scholar 

  13. Deissler RG, Taylor MF (1958) Analysis of turbulent flow and heat transfer in noncircular passages. NACA Technical Note 4384

  14. Mitsuishi N, Kitayama Y, Aoyagi Y (1966) Flow of power-law fluids in a duct of arbitrary cross section and triangular ducts. Int Chem Eng 8:168

    Google Scholar 

  15. Middleman S (1965) Flow of non-Newtonian fluids in narrow rectangular channels. Trans Soc Rheol 9(1):83–93

    Article  Google Scholar 

  16. Sparrow EM (1962) Laminar flow in isosceles triangular ducts. Am Inst Chem Eng J 8(5):599–604

    Article  Google Scholar 

  17. Beyer CE, Towsley FE (1952) The flow of polystyrene through rectangular channels. J Colloid Sci 7(3):236–243

    Article  Google Scholar 

  18. Hartnett JP, Kostic M (1985) Heat transfer to a viscoelastic fluid in laminar flow through a rectangular channel. Int J Heat Mass Transf 28(6):1147–1155

    Article  Google Scholar 

  19. Rao RB (1989) Laminar mixed convection heat transfer to viscoelastic fluids in a 5:1 rectangular channel. Int J Heat Fluid Flow 10(4):334–338

    Article  Google Scholar 

  20. Wheeler JA, Wissler EH (1965) The friction factor-Reynolds number relation for the steady flow of pseudo plastic fluids through rectangular ducts. Am Inst Chem Eng J 11:207–216

    Article  Google Scholar 

  21. Mitsuishi N, Aoyagi Y (1969) Non-Newtonian flow in non-circular ducts. Chem Eng Sci 24(2):309–319

    Article  Google Scholar 

  22. Ray S, Date AW (2003) Friction and heat transfer characteristics of flow through square duct with twisted tape insert. Int J Heat Mass Transf 46:889–902

    Article  MATH  Google Scholar 

  23. Oliver DR, Karim RB (1971) Laminar-flow non-Newtonian heat transfer in flattened tubes. Can J Chem Eng 49(2):236–240

    Article  Google Scholar 

  24. Siginer DA, Letelier MF (2005) Heat transfer in laminar flow of viscoelastic fluids in straight tubes of arbitrary shape. Annu Trans Nord Rheol Soc 13:137–145

    Google Scholar 

  25. Metzner AB, White JL, Denn MM (1966) Constitutive equations for viscoelastic fluids for short deformation periods and for rapidly changing flows: significance of the Deborah Number. Am Inst Chem Eng J 12(5):863–865

    Article  Google Scholar 

  26. Metzner AB, White JL (1965) Flow behavior of viscoelastic fluids in the inlet region of a channel. Am Inst Chem Eng J 11(6):989–995

    Article  Google Scholar 

  27. Oldroyd JG (1950) On the formulation of rheological equations of state. Proc R Soc Lond A200:523–541

    MathSciNet  Google Scholar 

  28. Karim RB (1973) Pressure drop of a viscoelastic system in flattened tubes. Sains Malays 2(2):77–81

    Google Scholar 

  29. Semjonow VV (1967) Pressure effect of viscosity for polymer fluids. Rheol Acta 6(2):171

    Article  Google Scholar 

  30. Oliver DR (1969) Secondary flow of viscoelastic liquids in flattened tubes. Trans Inst Chem Eng 47:T18

    Google Scholar 

  31. James PA (1970) Forced convection heat transfer in narrow passages. Can J Chem Eng 48:330–332

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Civil Engineering Department, Universiti Malaya, 50603, Kuala Lumpur, Malaysia

    Z. Ismail

  2. 53 Persiaran Zaaba, TTDI, 60000, Kuala Lumpur, Malaysia

    R. Karim

Authors
  1. Z. Ismail
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Karim
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Z. Ismail.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ismail, Z., Karim, R. Determination of optimum aspect ratio for laminar flow heat transfer of dilute viscoelastic solutions in flattened tube heat exchangers. Heat Mass Transfer 48, 1319–1331 (2012). https://doi.org/10.1007/s00231-012-0981-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-012-0981-2

Keywords

Search

Navigation