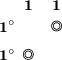The Noncommutative Geometry of Electrodynamics

Abstract

In the previous chapters we have described the general framework for the description of gauge theories in terms of noncommutative manifolds.

9.A Grassmann Variables, Grassmann Integration and Pfaffians

We will give a short introduction to Grassmann variables, and use those to find the relation between the Pfaffian and the determinant of an antisymmetric matrix.

For a set of anti-commuting Grassmann variables $\theta _i$, we have $\theta _i\theta _j = - \theta _j\theta _i$, and in particular, $\theta _i^2 = 0$. On these Grassmann variables $\theta _j$, we define an integral by

$$\begin{aligned} \int 1 d\theta _j = 0 ,\quad \int \theta _j d\theta _j= 1 . \end{aligned}$$

If we have a Grassmann vector $\theta$ consisting of $N$ components, we define the integral over $D[\theta ]$ as the integral over $d\theta _1\cdots d\theta _N$. Suppose we have two Grassmann vectors $\eta$ and $\theta$ of $N$ components. We then define the integration element as $D[\eta ,\theta ] = d\eta _1d\theta _1\cdots d\eta _Nd\theta _N$.

Consider the Grassmann integral over a function of the form $e^{\theta ^T\mathfrak {A}\eta }$ for Grassmann vectors $\theta$ and $\eta$ of $N$ components. The $N\times N$-matrix $\mathfrak {A}$ can be considered as a bilinear form on these Grassmann vectors. In the case where $\theta$ and $\eta$ are independent variables, we find

$$\begin{aligned} \int e^{\theta ^T\mathfrak {A}\eta } D[\eta ,\theta ] = \det \mathfrak {A}, \end{aligned}$$

(9.A.1)

where the determinant of $\mathfrak {A}$ is given by the formula

$$\begin{aligned} \det (\mathfrak {A}) = \frac{1}{N!} \sum _{\sigma ,\tau \in S_N} (-1)^{|\sigma |+|\tau |} \mathfrak {A}_{\sigma (1)\tau (1)}\cdots \mathfrak {A}_{\sigma (N)\tau (N)} , \end{aligned}$$

in which $S_N$denotes the set of all permutations of $\{1,2,\ldots ,N\}$. Now let us assume that $\mathfrak {A}$ is an antisymmetric $N\times N$-matrix $\mathfrak {A}$ for $N=2l$. If we then take $\theta =\eta$, we find

$$\begin{aligned} \int e^{\frac{1}{2}\eta ^T\mathfrak {A}\eta } D[\eta ] = {{\mathrm{Pf}}}(\mathfrak {A}) , \end{aligned}$$

(9.A.2)

where the Pfaffian of $\mathfrak {A}$ is given by

$$\begin{aligned} {{\mathrm{Pf}}}(\mathfrak {A}) = \frac{(-1)^l}{2^ll!} \sum _{\sigma \in S_{2l}} (-1)^{|\sigma |} \mathfrak {A}_{\sigma (1)\sigma (2)} \cdots \mathfrak {A}_{\sigma (2l-1)\sigma (2l)} . \end{aligned}$$

Finally, using these Grassmann integrals, one can show that the determinant of a $2l\times 2l$ skew-symmetric matrix $\mathfrak {A}$ is the square of the Pfaffian:

$$\begin{aligned} \det \mathfrak {A}= {{\mathrm{Pf}}}(\mathfrak {A})^2 . \end{aligned}$$

So, by simply considering one instead of two independent Grassmann variables in the Grassmann integral of $e^{\theta ^T\mathfrak {A}\eta }$, we are in effect taking the square root of a determinant.

Notes

Section 9.1 The Two-Point Space

• 1. The two-point space was first studied in [1, 2].

• 2. The need for KO-dimension $6$ for the noncommutative description of the Standard Model has been observed independently by Barrett [3] and Connes [4].

• 3. In [5, Chap. 9] a proof is given for the claim that the inner fluctuation $\omega + J\omega J^{-1}$ vanishes for commutative algebras. The proof is based on the assumption that the left and right action can be identified, i.e. $a=a^0$, for a commutative algebra. Though this holds in the case of the canonical triple describing a spin manifold, it need not be true for arbitrary commutative algebras. Indeed, the almost-commutative manifold$M \times F_X$ provides a counter-example. What we can say about a commutative algebra, is that there exist no non-trivial inner automorphisms. Thus, it is an important insight that the gauge group $\mathfrak {G}(\mathcal {A},\mathcal {H};J)$ from Definition 6.4 is larger than the group of inner automorphisms, so that a commutative algebra may still lead to a non-trivial (necessarily abelian) gauge group.

• 4. It is shown in [6] that one can also obtain abelian gauge theories from a one-point space when one works with real algebras (cf. Sect.  3.3).

Section 9.2 Electrodynamics

• 5. Earlier attempts at a unified description of gravity and electromagnetism originate from the work of Kaluza [7] and Klein [8] in the 1920s. In their approach, a new (compact) fifth dimension is added to the $4$-dimensional spacetime $M$. The additional components in the $5$-dimensional metric tensor are then identified with the electromagnetic gauge potential. Subsequently, it can be shown that the Einstein equations of the $5$-dimensional spacetime can be reduced to the Einstein equations plus the Maxwell equations on $4$-dimensional spacetime.

• 6. An interesting question that appears in the context of this Chapter is whether it is possible to describe the abelian Higgs mechanism (see e.g. [9, Sect.  8.3]) by an almost-commutative manifold. As already noticed, for $M \times F_{\scriptscriptstyle ED}$ no scalar fields $\Phi$ are generated since $A_F$ commutes with $D_F$. In terms of the Krajewski diagram for $M \times F_{\scriptscriptstyle ED}$,

  

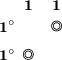
  it follows that a component that runs counterdiagonally fails on the first-order condition (cf. Lemma 3.10). One is therefore tempted to look at the generalization of inner fluctuations to real spectral triples that do not necessarily satisfy the first-order condition, as was proposed in [10]. This generalization is crucial in the applications to Pati–Salam unification (see Note 13 on page 223), but also in the present case one can show that non-zero off-diagonal components in (9.2.3) then generate a scalar field for which the spectral action yields a spontaneous breaking of the abelian gauge symmetry.

Appendix 9.A Grassmann Variables, Grassmann Integration and Pfaffians

• 7. For more details on Grassmann variables we refer to [11].