Abstract
In this paper, we give an introduction to the theory of overconvergent modular symbols and their connection to p-adic L-functions. Alongside the theory, we describe many explicit examples to illustrate the concrete nature of this subject, and give algorithms for computing inside of these infinite-dimensional spaces.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
These notes arose from a series of lectures given by the author and Glenn Stevens at the Arizona Winter School in March 2011, and then were further refined after a second lecture series by the author at the summer school attached to the conference Computations with Modular Forms in August 2011 at Heidelberg University.
- 2.
- 3.
We note that the background needed to study overconvergent modular symbols is significantly less substantial than the background needed to study the corresponding theory of overconvergent modular forms. See Sect. 3.1 for a brief comparison between the two theories.
- 4.
More honestly, only choose pairs of rational numbers which are Γ 0(11)-equivalent under linear fractional transformations. See Footnote 6 for more details.
- 5.
Here is a heuristic argument for this equality:
$$\begin{aligned} 2 \pi \mathrm {i}\int_{\mathrm {i}\,\infty}^0 f(z)\, \mathrm{d}z &= 2 \pi \mathrm {i}\int_{\mathrm {i}\infty}^0 \sum_n a_n \mathrm{e}^{2\pi \mathrm {i}nz}\, \mathrm{d}z = 2 \pi \mathrm {i}\sum _n a_n \int_{\mathrm {i}\infty}^0 \mathrm{e}^{2\pi \mathrm {i}nz}\, \mathrm{d}z \\ &= \sum_n \frac{a_n}{n} \mathrm{e}^{2\pi \mathrm {i}nz} \bigg|_{\mathrm {i}\,\infty}^0\, \mathrm{d}z = \sum_n \frac{a_n}{n} = L(f,1). \end{aligned}$$However, this argument suffers from serious convergence issues.
- 6.
The reason this period integral is not a \(\mathbb {Z}\)-multiple of \(\varOmega_{E}^{+}\) is related to the fact that ∞ and 0 are not Γ 0(11)-equivalent. Computing the period integrals between all cusps would yield a lattice which contains our lattice with finite index.
- 7.
- 8.
Note that there are no cusp forms of weight 2 and level Γ 0(2), and so it should not be a surprise that there are no symbols of the form ψ f .
- 9.
See [PS11, Sect. 2.3] for the details of the following construction.
- 10.
For completeness, let’s mention that D 1, D 2 and D 3 do not generate freely over \(\mathbb {Z}[\varGamma_{0}(11)]\). Indeed, there is one relation between these divisors that is easy to see via the fundamental domain. Namely, if we sum up over the boundary of the fundamental domain, we get 0. Explicitly, we have
$$\begin{aligned} &\bigl(\{0\}-\{\infty\} \bigr) + \bigl(\{\infty\}-\{-1\} \bigr) + \biggl(\{-1\}- \biggl\{ -\frac{2}{3} \biggr\} \biggr) + \biggl( \biggl\{ - \frac {2}{3} \biggr\} - \biggl\{ -\frac{1}{2} \biggr\} \biggr) \\ &\quad {}+ \biggl( \biggl\{ -\frac{1}{2} \biggr\} - \biggl\{ -\frac{1}{3} \biggr\} \biggr) + \biggl( \biggl\{ -\frac{1}{3} \biggr\} -\{0\} \biggr) = 0 \end{aligned}$$and re-writing this in terms of our generators gives
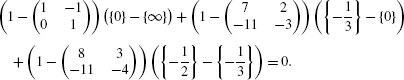
Further, one can check that this is the only relation these divisors satisfy. This relation plays no role when considering modular symbols with trivial coefficients, but once the coefficients have a non-trivial matrix action, this more complicated relation must be considered.
- 11.
We note that if \(\mathcal{H}\) denotes the upper-half plane and \(\widetilde{V}\) is the associated locally constant sheaf of V on \(\mathcal{H}/\varGamma\), then there is a canonical isomorphism
$$\mathrm{Symb}_\varGamma(V)\, \cong H^1_c ( \mathcal{H} / \varGamma ,\widetilde{V} ) , $$provided that the order of any torsion element of Γ acts invertibly on V (see [Ash86, Proposition 4.2]). In these notes, we however focus on the explicit description of modular symbols given by maps rather than by cohomology classes.
- 12.
Hint: φ 1 is nothing other than the modular symbol defined earlier which extends to all of Δ!
- 13.
For a reference, see [BD, Proposition 2.5].
- 14.
We are side stepping the appropriate normalization of this period which would be needed to get μ-invariants correct.
- 15.
A p-ordinary modular form is a normalized eigenform f such that a p (f) is a p-adic unit. Note that a p (f) is a priori only in \(\overline{\mathbb {Q}}\), but again we are implicitly viewing it as a p-adic number via our fixed embedding of \(\overline{\mathbb {Q}}\) into \(\overline{\mathbb {Q}}_{p}\) from above.
- 16.
A classical form of level Γ cannot have a U p -eigenvalue with p-adic valuation larger than k−1 (see Sect. 3.7 for details). So it’s only forms of slope k−1 that are not completely explained by this theorem. These are called the critical slope forms.
- 17.
We also note that spaces of overconvergent modular symbols contain the same system of Hecke-eigenvalues as the corresponding space of overconvergent modular forms (see [PS, Theorem 7.1]).
- 18.
Here’s a more natural way to see the map ρ k . Consider the span of the functions 1,z,…,z k inside of A k . This span is stable under the weight k action, and its dual is simply V k . Thus dualizing this inclusion gives a map from D k to V k which can be seen to be precisely the map ρ k .
- 19.
Note that D k is equipped with a natural Γ 0-action, but this action does not extend to Γ.
- 20.
Recall that \(V_{k} = \mathrm{Sym}^{k} (\mathbb {Q}_{p}^{2} )\) and so modular symbols in \(\mathrm{Symb}_{\varGamma_{0}}(V_{k})\) correspond to modular forms of weight k+2, and not weight k.
- 21.
So far we’ve only defined slopes of modular forms. But if M is any \(\mathbb {Z}_{p}\)-module with an action of U p , one defines the slope of an eigenvector of U p as the p-adic valuation of the associated eigenvalue. Moreover, for any real number h, we write M (<h) to denote the subspace on which U p acts with slope less than h.
- 22.
- 23.
Note that in Coleman’s world, classical forms are a subspace of overconvergent forms. However, in our setting, classical modular symbols are a quotient of overconvergent modular symbols.
- 24.
Note that we are assuming that g is an eigenform on Γ 0 and not on Γ. If one is starting off with a form on Γ, to form its p-adic L-function, one must choose a p-stabilization of this form to Γ 0. See Sect. 5.1 for details.
- 25.
We note that this theorem is off by a sign from the corresponding theorems in [PS11] and [PS]. The underlying reason for this discrepancy is that in this paper we defined ψ f ({s}−{r}) in terms of the path integral from r to s rather than from s to r. But, more importantly, we should mention that “the” p-adic L-function of g depends upon the choice of \(\varOmega_{g}^{+}\) and \(\varOmega_{g}^{-}\), each of which is only well-defined up to a p-adic unit. Thus, any ambiguity of sign can be absorbed into the choice of these periods.
- 26.
Because of convergence issues, there is no reason that such an expansion should even exist, but let’s just imagine so anyway.
- 27.
If this were not true, we could use the other Hecke operators to kill off the other overconvergent eigensymbols of slope 0 in the expansion of Ψ without changing the fact that Ψ lifts φ.
- 28.
Writing \(\mu_{f}(a+p^{n}\mathbb {Z}_{p})\) is a bit of an abusive of notation. What is meant here is the value obtained when evaluating μ f on the characteristic function of \(a+p^{n}\mathbb {Z}_{p}\).
- 29.
Note then that f β is a critical slope form, and in fact, all critical slope forms arise in this manner.
- 30.
In fact, this definition only tells us the value of μ f on locally constant functions. However, since the values given are bounded (α is a unit!), standard arguments via Riemann sums allow us to integrate μ f against any continuous function (and thus against any locally analytic function).
References
A. Ash, G. Stevens, Modular forms in characteristic ℓ and special values of their L-functions. Duke Math. J. 53(3), 849–868 (1986)
A. Atkin, W.C.W. Li, Twists of newforms and pseudo-eigenvalues of W-operators. Invent. Math. 48(3), 221–243 (1978)
J. Bellaïche, Critical p-adic L-functions. Invent. Math. 189(1), 1–60 (2012)
J. Bellaïche, S. Dasgupta, The p-adic L-function of evil Eisentein series. Preprint
R. Coleman, Classical and overconvergent modular forms. Invent. Math. 124(1–3), 215–241 (1996)
R. Coleman, p-adic Banach spaces and families of modular forms. Invent. Math. 127(3), 417–479 (1997)
M. Greenberg, Lifting modular symbols of noncritical slope. Isr. J. Math. 161, 141–155 (2007)
H. Hida, Galois representations into \({\rm GL}_{2}({\bf Z}_{p}[[X]])\) attached to ordinary cusp forms. Invent. Math. 85(3), 545–613 (1986)
H. Hida, Iwasawa modules attached to congruences of cusp forms. Ann. Sci. Éc. Norm. Super. 19(2), 231–273 (1986)
Y. Manin, Parabolic points and zeta functions of modular curves. Izv. Akad. Nauk SSSR, Ser. Mat. 36, 19–66 (1972)
B. Mazur, Courbes elliptiques et symboles modulaires, in Séminaire Bourbaki, 24ème année (1971/1972), Exp. No. 414. Lecture Notes in Math., vol. 317 (Springer, Berlin, 1973), pp. 277–294
R. Pollack, G. Stevens, Overconvergent modular symbols and p-adic L-functions. Ann. Sci. Éc. Norm. Supér. 44(4), 1–42 (2011)
R. Pollack, G. Stevens, Critical slope p-adic L-functions. J. Lond. Math. Soc. 87(2), 428–452 (2013)
W. Stein, Sage: Open Source Mathematical Software. http://www.sagemath.org
G. Stevens, Rigid analytic modular symbols, unpublished notes (1994)
Acknowledgements
The author acknowledges support from NSF grant DMS-1001768.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2014 Springer International Publishing Switzerland
About this paper
Cite this paper
Pollack, R. (2014). Overconvergent Modular Symbols. In: Böckle, G., Wiese, G. (eds) Computations with Modular Forms. Contributions in Mathematical and Computational Sciences, vol 6. Springer, Cham. https://doi.org/10.1007/978-3-319-03847-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-03847-6_3
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-03846-9
Online ISBN: 978-3-319-03847-6
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)