Abstract
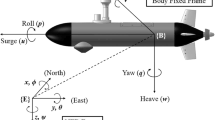
In this paper, an algorithm for submersible autonomous robotic vehicle (SARV) is proposed using a derivative feedback-based optimal control technique to track the yaw orientation. The optimal control law is obtained by using a linear quadratic regulator (LQR). A linear matrix inequalities (LMI) approach is used to develop a control algorithm and the realization is carried out using semi-definite programming (SDP). An optimal control action is subjected to a derivative controller for smooth tracking of desired yaw. It is found that energy consumption exerted due to the control input is reduced because of the derivative controller. YALMIP toolbox is used to solve the LMI using MATLAB/Simulink in realizing the control law. The simulation results exhibit that the control algorithm is capable of tracking the desired yaw. A difference in tracking of yaw in the presence of derivative feedback and the absence of derivative feedback is clearly shown and discussed. It is also shown that the tracking of desired yaw has a better performance in terms of derivative feedback.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Valeriano Y, Fernandez A, Hernandez L, Prieto P (2016) Yaw controller in sliding mode for underwater autonomous vehicle. IEEE Lat Am Trans 14(3):1213–1220. IEEE
Yue-Sheng L, Xiu-Ping W, Shi-Wei L (2012) H∞ heading control of AUV based on state observers. In: Future control and automation, vol 122. Springer, Berlin, pp 165–174
Rhoads B, Mezic I, Poje AC (2013) Minimum time heading control of underpowered vehicles in time-varying ocean currents. Ocean Eng 66:12–31. Elsevier
Mahapatra S, Subudhi B (2021) Nonlinear matrix inequality approach based heading control for an autonomous underwater vehicle with experimental realization. IFAC J Syst Control 16. Elsevier
Petrich J, Stilwell DJ (2011) Robust control for an autonomous underwater vehicle that suppresses pitch and yaw coupling. Ocean Eng 38(1):197–204. Elsevier
Mahapatra S, Subudhi B (2017) Design of a steering control law for an autonomous underwater vehicle using nonlinear H∞ state feedback technique. Nonlinear Dyn 90(2):837–854. Springer
Mahapatra S, Subudhi B (2018) Nonlinear H∞ state and output feedback control schemes for an autonomous underwater vehicle in the dive plane. Trans Inst Meas Control 40(6):2024–2038
Mahapatra S, Subudhi B, Rout R (2016) Diving control of an autonomous underwater vehicle using nonlinear H∞ measurement feedback technique. In: OCEANS 2016-Shanghai. IEEE, pp 1–5
Mahapatra S, Subudhi B (2018) Design and experimental realization of a backstepping nonlinear H∞ control for an autonomous underwater vehicle using a nonlinear matrix inequality approach. Trans Inst Meas Control 40(11):3390–3403
Rout R, Subudhi B, Mahapatra S (2016) Development of a narmax based constraint-adaptive heading controller for an autonomous underwater vehicle. In: OCEANS 2016-Shanghai. IEEE, pp 1–5
Zhang J, Swain AK, Nguang SK (2016) Robust observer-based fault diagnosis for nonlinear systems using MATLAB®. Springer, Switzerland
Abdelaziz T (2010) Optimal control using derivative feedback for linear systems. Proc Inst Mech Eng, Part I, J Syst Control Eng 224:185–202
Beteto MA, Assuncao E, Teixeira MC, Silva ER, Buzachero LF, Caun RP (2018) New design of robust LQR-state derivative controllers via LMIs. IFAC-PapersOnLine 51:422–427
Silvestre C (2000) Multi-objective optimization theory with applications to the integrated design of controllers/plants for autonomous vehicles, dissertation
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Vadapalli, S., Mahapatra, S. (2023). State Derivative Optimal Control Law for Submersible Autonomous Robotic Vehicle in Steering Plane. In: Chakraborty, B., Biswas, A., Chakrabarti, A. (eds) Advances in Data Science and Computing Technologies. ADSC 2022. Lecture Notes in Electrical Engineering, vol 1056. Springer, Singapore. https://doi.org/10.1007/978-981-99-3656-4_13
Download citation
DOI: https://doi.org/10.1007/978-981-99-3656-4_13
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-99-3655-7
Online ISBN: 978-981-99-3656-4
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)