Keywords

1 Introduction

One of the effective and practical methods used in the analysis of shear wall-frame systems is the continuum method. There have been many studies dealing with the method which was first used by Chitty in 1940 [1]. These studies include various situations such as static analysis and dynamic analysis [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Stafford Smith et al. proposed an approximate method for calculating the displacement of the high-rise buildings under triangular distributed loads, taking account of the continuum model [27]. Heidebrecht ve Rutenberg proposed an approach to determine the performance of frame systems by utilizing the intersorey drift ratios. In the study, the frame system was modeled as an equivalent shear beam [28]. Gülkan and Akkar proposed a method for determining IDR of the structures of which the bearing system consisting of frames. In the study, the multistorey frame system was idealized as an equivalent shear beam to achieve the maximum IDR [29]. In Miranda and Akkar's work, they proposed a method of using graphs for response spectrum analysis by using the flexural-shear beam to obtain the IDR [16]. Xie and Wen used the Timoshenko beam model to calculate the IDRs of multistorey structures [30]. Khaloo and Khosravi investigated the effect of modes in the structures under near fault pulse like ground motions. In the study, the structure was idealized as an equivalent flexural shear beam according to the continuum method [31].

Yang, Pan and Li used the flexural-shear beam model to determine the maximum IDR of the structures under near-fault ground motion [32].

Fardipour et al. proposed a practical method of determining the maximum IDR for Australia, depending on the height of the building, the type of bearing system, the change in the stiffness and the mass [33]. Shodja and Rofooei developed a method based on the discrete mass model for determining the drift spectrum. In the method, the variation of the structure stiffness along the height of the structure is also taken into consideration [34]. Tekeli, Atımtay and Turkmen proposed a method for determining the lateral displacement of the reinforced concrete frame structures under the static loads. In the method, the frame system was considered as an equivalent shear frame [35]. In this study, a method has been proposed in which the maximum displacement and the maximum IDR are quickly and practically determined by means of tables for both Response Spectrum Analysis and Equivalent Static Loads Method. Subsequent paragraphs, however, are indented.

In creating the tables for the method, it is assumed that

  • The properties of the building is constant and the mass is uniformly distributed up to the height of the building.

  • The shear deformations of the columns, shear walls and the beams are neglected.

  • The axial deformations of the beams are neglected.

  • The torsion is neglected.

  • The material is considered as linear elastic and the nonlinear geometric effects are ignored.

  • Slabs are assumed infinitely rigid in their own planes.

2 Response Spectrum Analysis by the Presented Method

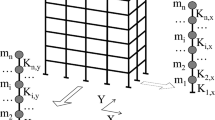
The reinforced concrete multistorey building can be modeled as an equivalent flexural-shear beam as seen in Fig. 1.

Fig. 1
An illustration presents how the rectangular-shaped multi-story building is equivalent to the structure of the building with a height of H and shear stiffness K subscript s.

The equivalent flexural-shear beam model of the structure

Full size image

In accordance with this model, the 4th order parabolic partial differential equation of the system with undamped free vibration is written as follows.

$$ \left( {{\text{EI}}} \right)\frac{{{ }\partial^{4} {\text{U}}}}{{\partial {\text{z}}^{4} }} - {\text{K}}_{{\text{s}}} \frac{{{ }\partial^{2} {\text{U}}}}{{\partial {\text{z}}^{2} }} + \frac{{\text{m}}}{{\text{h}}}\frac{{{ }\partial^{2} {\text{U}}}}{{\partial {\text{t}}^{2} }} = 0 $$
(1)

where z is the vertical axis, and m/h is the distributed mass up to the height of the building. Ks is the equivalent shear stiffness and it is calculated by the following equation [4, 12].

$$ {\text{K}}_{{\text{s}}} = \frac{{12{\text{E}}}}{{{\text{h}}\left( {\frac{1}{{\text{s}}} + \frac{1}{{\text{r}}}} \right)}} $$
(2)

where h is the storey height, E is the modulus of elasticity, r and s are the contributions of columns and beams to the shear stiffness which are calculated by the following equations.

$$ {\text{s}} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{p}}} \frac{{{\text{I}}_{{{\text{cj}}}} }}{{\text{h}}} $$
(3)
$$ {\text{r}} = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{g}}} \frac{{{\text{I}}_{{{\text{bj}}}} }}{{{\text{l}}_{{\text{i}}} }} $$
(4)

In the combined shear wall- frame system in Fig. 2, the shear stiffness is calculated approximately by the following equation.

$$ {\text{K}}_{{\text{s}}} = \frac{{1.1{\text{Er}}}}{{\text{h}}} $$
(5)
Fig. 2
A diagram presents a multi-story building in the Y Z direction, which has several beams and frames with combined rectangular-shaped wall frame systems.

The combined shear wall-frame system

Full size image

Here 1.1 is the correction factor.

The total bending stiffness of the shear walls and columns is shown as (EI) and it is calculated by the following equation [4, 12].

$$ \left( {{\text{EI}}} \right) = \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{u}}} {\text{EI}}_{{{\text{wj}}}} + \mathop \sum \limits_{{{\text{j}} = 1}}^{{\text{p}}} {\text{EI}}_{{{\text{cj}}}} $$
(6)

If the partial differential Eq. (1) is separated into the variables using the Eq. (7), the ordinary differential equations in (8) and (9) are obtained.

$$ {\text{U}}\left( {{\text{z}},{\text{t}}} \right) = {\text{Y}}\left( {\text{z}} \right){\text{T}}\left( {\text{t}} \right) $$
(7)
$$ \left( {{\text{EI}}} \right)\frac{{ {\text{d}}^{4} {\text{y}}}}{{{\text{dz}}^{4} }} - {\text{K}}_{{\text{s}}} \frac{{ {\text{d}}^{2} {\text{y}}}}{{{\text{dz}}^{2} }} - \frac{{{\text{m}}\upomega ^{2} }}{{\text{h}}}\frac{{ {\text{d}}^{2} {\text{y}}}}{{{\text{dt}}^{2} }} = 0 $$
(8)
$$ \frac{{{\text{ d}}^{2} {\text{y}}}}{{{\text{dt}}^{2} }} +\upomega ^{2} {\text{y}} = 0 $$
(9)

Here, y shows the modal shape and ω denotes the angular frequency. The boundary conditions of the 4th order constant coefficient homogeneous ordinary differential Eq. (8) are that, the displacement and rotation at the base of the structure are zero and the bending moment and the shear force at the top point are zero. These boundary conditions are given below.

$$ {\text{y}}\left( 0 \right) = 0 $$
(10)
$$ \frac{{{\text{dy}}\left( 0 \right)}}{{{\text{dz}}}} = 0 $$
(11)
$$ \left( {{\text{EI}}} \right)\frac{{{\text{ d}}^{2} {\text{y}}\left( {\text{H}} \right)}}{{{\text{dz}}^{2} }} $$
(12)
$$ \left( {{\text{EI}}} \right)\frac{{{\text{ d}}^{3} {\text{y}}\left( {\text{H}} \right)}}{{{\text{dz}}^{3} }} - {\text{K}}_{{\text{s}}} \frac{{{\text{dy}}\left( {\text{H}} \right)}}{{{\text{dz}}}} = 0 $$
(13)

To make differential Eq. (8) dimensionless, the following transformation can be used.

$$\upvarepsilon = \frac{{\text{z}}}{{\text{H}}} $$
(14)

Equation (15) is obtained when the transformation in Eq. (14) is applied to the Eq. (8).

$$ \frac{{{\text{ d}}^{4} {\text{y}}}}{{{\text{d}}\upvarepsilon ^{4} }} - {\text{k}}^{2} \frac{{{\text{ d}}^{2} {\text{y}}}}{{{\text{d}}\upvarepsilon ^{2} }} - {\alpha y} = 0 $$
(15)

With the aim of the reduction, the parameters in Eq. (15) are defined as follows

$$ {\text{k}} = {\text{H}}\sqrt {\frac{{{\text{K}}_{{\text{s}}} }}{{\left( {{\text{EI}}} \right)}}} $$
(16)
$$ {\upalpha } = \frac{{{\text{mH}}^{4} {\upomega }^{2} }}{{\left( {{\text{EI}}} \right){\text{h}}}} $$
(17)

The solution of the differential Eq. (15) is obtained as follows.

$$ {\text{y}}\left(\upvarepsilon \right) = {\text{c}}_{1} \cosh \left( {{\text{a}}_{1}\upvarepsilon } \right) + {\text{c}}_{2} {\text{sinh}}\left( {{\text{a}}_{1}\upvarepsilon } \right) + {\text{c}}_{3} \cos \left( {{\text{a}}_{2}\upvarepsilon } \right) + {\text{c}}_{4} {\text{sin}}\left( {{\text{a}}_{2}\upvarepsilon } \right) $$
(18)

Here, a1 and a2 are shown below.

$$ {\text{a}}_{1} = \sqrt {\frac{{{\text{k}}^{2} + \sqrt {{\text{k}}^{4} + 4{\text{k}}^{2} {\upalpha }} }}{2}} $$
(19)
$$ {\text{a}}_{2} = \sqrt {\frac{{ - {\text{k}}^{2} + \sqrt {{\text{k}}^{4} + 4{\text{k}}^{2} {\upalpha }} }}{2}} $$
(10)

The boundary conditions given in the Eqs. (10), (11), (12) and (13) are written in dimensionless form as follows.

$$ y\left( 0 \right) = 0 $$
(21)
$$ \frac{1}{H}\frac{dy\left( 0 \right)}{{d\upvarepsilon }} = 0 $$
(22)
$$ \frac{{\left( {EI} \right)}}{{H^{2} }}\frac{{ d^{2} y\left( 1 \right)}}{{d\upvarepsilon ^{2} }} $$
(23)
$$ \frac{{ d^{3} y\left( 1 \right)}}{{d\upvarepsilon ^{3} }} - k^{2} \frac{dy\left( 1 \right)}{{d\upvarepsilon }} = 0 $$
(24)

If the non-dimensional boundary conditions are written in Eq. (18), the following frequency equation is obtained.

$$ \begin{aligned} f & = \left[ {a_{2}^{4} + k^{2} a_{2}^{2} + a_{1}^{4} - k^{2} a_{1}^{2} } \right] + \left[ {2a_{1}^{2} a_{2}^{2} + k^{2} a_{1}^{2} - k^{2} a_{2}^{2} } \right]\cosh \left( {a_{1} } \right)\cos \left( {a_{2} } \right) \\ & \quad - \left[ { - a_{2}^{3} a_{1} + a_{1}^{3} a_{2} - k^{2} a_{1} a_{2} } \right]\sinh \left( {a_{1} } \right)\sin \left( {a_{2} } \right) \\ & = 0 \\ \end{aligned} $$
(25)

If the necessary arrangements are made in this frequency equation, the following equation is obtained.

$$ f = 2\alpha + \left[ {2\alpha + k^{4} } \right]\cosh \left( {a_{1} } \right)\cos \left( {a_{2} } \right) + (k^{2} \sqrt \alpha )\sinh \left( {a_{1} } \right)\sin \left( {a_{2} } \right) = 0 $$
(26)

After calculating α values which make the Eq. (26) zero, with the help of Eq. (17), the natural vibration periods are found as follows.

$$ T_{i} = Z_{i} H^{2} \sqrt {\frac{m}{{h\left( {EI} \right)}}} $$
(27)

The Zi period parameters in Eq. (27) are given in Table 1 depending on the k parameter for the first three modes.

Table 1 Z values for the first three modes
Full size table

Using the frequency equation and boundary conditions, the mode shapes are found by the following equation.

$$ y = \left[ {\cosh \left( {a_{1}\upvarepsilon } \right) - \cos \left( {a_{2}\upvarepsilon } \right)} \right] + E\left[ {\sinh \left( {a_{1}\upvarepsilon } \right) - \frac{{a_{1} }}{{a_{2} }}\sin \left( {a_{2}\upvarepsilon } \right)} \right] $$
(28)

E can be calculated by the following equation.

$$ E = - \frac{{\left[ {a_{1}^{2} \cosh \left( {a_{1} } \right) + a_{2}^{2} \cos \left( {a_{2} } \right)} \right]}}{{\left[ {a_{1}^{2} \sinh \left( {a_{1} } \right) + a_{1} a_{2} \sin \left( {a_{2} } \right)} \right]}} $$
(29)

The modal participation factor required for the Response Spectrum Analysis is calculated by the following equation as known from the literature [36].

$$ \Gamma_{i} = \frac{{\frac{m}{h}\mathop \int\nolimits_{0}^{1} y_{i} }}{{\frac{m}{h}\mathop \int\nolimits_{0}^{1} y_{i}^{2} }} $$
(30)

For the i-th mode shape, the maximum displacement is calculated by the Eq. (31).

$$ dep_{i} = \Gamma_{i} y_{i} \left( 1 \right)S_{di} = \mu_{i} S_{di} $$
(31)

where Sdi is the displacement spectral ordinate for the i-th mode and it can be obtained either from the design spectrum, or from the displacement spectrum created for a particular earthquake record.

The μi values given here are calculated for the first three modes and they are given in Table 2.

Table 2 μ displacement coefficients for the first three modes
Full size table

By using the maximum displacements obtained for the three modes and with the help of the SRSS rule, the maximum displacements is calculated by Eq. (32).

$$ d = \sqrt {\left( {dep_{1}^{2} + dep_{2}^{2} + dep_{3}^{2} } \right)} $$
(32)

For the dimensionless IDR, if the derivative of Eq. (28) is taken the following equation is obtained.

$$ \frac{1}{H}\frac{{dy\left(\upvarepsilon \right)}}{{d\upvarepsilon }} = \frac{1}{H}\left[ {a_{1} \sinh \left( {a_{1}\upvarepsilon } \right) + a_{2} \sin \left( {a_{2}\upvarepsilon } \right)} \right] + E\left[ {a_{1} \cosh \left( {a_{1}\upvarepsilon } \right) - a_{1} \cos \left( {a_{2}\upvarepsilon } \right)} \right] $$
(33)

To find the maximum value of the Eq. (33), the derivation must be taken and equalized to zero.

$$ \frac{1}{H}\frac{{ d^{2} y_{i} }}{{d\upvarepsilon ^{2} }} = \frac{1}{H}\left[ {a_{1}^{2} \cosh \left( {a_{1}\upvarepsilon } \right) + a_{2}^{2} \cos \left( {a_{2}\upvarepsilon } \right)} \right] + E\left[ {a_{1}^{2} \sinh \left( {a_{1}\upvarepsilon } \right) + a_{1} a_{2} \sin \left( {a_{2}\upvarepsilon } \right)} \right] = 0 $$
(34)

Ɛimax which makes the Eq. (34) equal to zero is different for three modes. For the Ɛ values, which make the IDR maximum in related mode, IDRs for the other modes are calculated by the equation below

$$ drift_{ij} = \Gamma_{i} \frac{1}{H}\left( {\frac{{dy_{i} \left( {\upvarepsilon _{j\max } } \right)}}{{d\upvarepsilon }}} \right)S_{di} = \beta_{ij} S_{di} \quad i = 1,2,3\;\;j = 1,2,3 $$
(35)

The β values in Eq. (35) are given in Tables 3, 4 and 5 considering the location of the maximum IDR in the first three modes. Also in Tables 6, 7 and 8, locations of maximum IDRs are given for the first three modes.

Table 3 β values for the first mode
Full size table
Table 4 β values for the second mode
Full size table
Table 5 β values for the third mode
Full size table
Table 6 Location of the maximum IDR for the first mode
Full size table
Table 7 Location of the maximum IDR for the second mode
Full size table
Table 8 Location of the maximum IDR for the third mode
Full size table

In this case, IDR values where the maximum IDR of the related mode is located are calculated according to the SRSS rule for the first three modes by the following equations.

$$ dr_{1} = \sqrt {\left( {drift_{11}^{2} + drift_{21}^{2} + drift_{31}^{2} } \right)} $$
(36)
$$ dr_{2} = \sqrt {\left( {drift_{12}^{2} + drift_{22}^{2} + drift_{32}^{2} } \right)} $$
(37)
$$ dr_{3} = \sqrt {\left( {drift_{13}^{2} + drift_{23}^{2} + drift_{33}^{2} } \right)} $$
(38)

And eventually, the maximum IDR is obtained as the largest of these three values.

$$ dr_{\max } = \max (dr_{1} ,dr_{2,} ,dr_{3)} $$
(39)

3 Equivalent Static Load Analysis by the Presented Method

The shear wall-frame system under the triangular distributed load which represent the equivalent static loads is given in the Fig. 3.

Fig. 3
A diagram presents a multi-story building in the Y Z direction, which combines several beams and frames with a rectangular wall frame and a load that is dispersed triangularly.

The shear wall-frame system under the triangular distributed load

Full size image

In this case, the horizontal equilibrium equation is written as follows.

$$ \left( {EI} \right)\frac{{ d^{4} y}}{{dz^{4} }} - K_{s} \frac{{ d^{2} y}}{{dz^{2} }} = q\frac{z}{H} $$
(40)

The boundary conditions of Eq. (40) are Eqs. (10), (11), (12) and (13).

To make the Eq. (40) dimensionless, the transform in Eq. (14) is used.

$$ \frac{{ d^{4} y}}{{d\upvarepsilon ^{4} }} - k^{2} \frac{{ d^{2} y}}{{d\upvarepsilon ^{2} }} = q\frac{{H^{4} }}{EI}\upvarepsilon $$
(41)

The dimensionless parameter k is defined by the Eq. (16).

Equation (43) is obtained if the following definition is made in Eq. (41).

$$ A = q\frac{{H^{4} }}{EI} $$
(42)
$$ \frac{{ d^{4} y}}{{d\upvarepsilon ^{4} }} - k^{2} \frac{{ d^{2} y}}{{d\upvarepsilon ^{2} }} = A\upvarepsilon $$
(43)

The solution of the 4th order constant-coefficient nonhomogeneous differential equation in (43) is obtained as follows.

$$ y\left(\upvarepsilon \right) = c_{1} + c_{2}\upvarepsilon + c_{3} \cosh \left( {k\upvarepsilon } \right) + c_{4} \sinh \left( {k\upvarepsilon } \right) - A\frac{{\upvarepsilon ^{3} }}{{6k^{2} }} $$
(44)

If the dimensionless boundary conditions in Eqs. (21), (22), (23) and (24) are applied in the Eq. (44), the displacement function is obtained as follows.

$$ y\left(\upvarepsilon \right) = S_{1} \left[ {1 - \cosh \left( {k\upvarepsilon } \right)} \right] + S_{2} \left[ {\upvarepsilon - \frac{1}{k}\sinh \left( {k\upvarepsilon } \right)} \right] - A\frac{{\upvarepsilon ^{3} }}{{6k^{2} }} $$
(45)

Here S1 and S2 are defined as below.

$$ {\text{S}}_{1} = {\text{A}}\left[ {\frac{{\frac{1}{{{\text{k}}^{2} }} - \left[ {\frac{1}{{{\text{k}}^{3} }} - \frac{1}{{2{\text{k}}}}} \right]\sin \left( {\text{k}} \right)}}{{{\text{k}}^{2} \cos \left( {\text{k}} \right)}}} \right] $$
(46)
$$ S_{2} = A\left[ {\frac{1}{{k^{4} }} - \frac{1}{{2k^{2} }}} \right] $$
(47)

In the Equivalent Static Loads Method, the following equation can be written for the base shear force.

$$ V_{b} = \frac{qH}{2} $$
(48)

Equation (49) is obtained by using the Eqs. (42) and (48).

$$ A = \frac{{2V_{b} H^{3} }}{EI} $$
(49)

With the help of Eq. (27), EI is obtained as follows.

$$ EI = Z_{1}^{2} H^{4} \frac{m}{{T_{1}^{2} h}} $$
(50)

Equation (51) is written by using Eqs. (49) and (50).

$$ A = \frac{{2V_{b} T_{1}^{2} h}}{{Z_{1}^{2} Hm}} $$
(51)

The total mass of the building can be written as:

$$ M = \frac{Hm}{h} $$
(52)

Equation (53) can be written by the help of Eq. (52)

$$ {\text{A}} = \frac{{2{\text{V}}_{{\text{b}}} {\text{T}}_{1}^{2} }}{{{\text{Z}}_{1}^{2} {\text{M}}}} $$
(53)

According to the Equivalent Static Loads Method, base shear force can be written as follows.

$$ V_{b} = S_{a1} M $$
(54)

Here, Sa1 represents the design spectral acceleration value for the first mode.

Equation (55) is obtained if the Eq. (54) is written in Eq. (53).

$$ {\text{A}} = \frac{{2{\text{S}}_{{{\text{a}}1}} {\text{T}}_{1}^{2} }}{{{\text{Z}}_{1}^{2} }} $$
(55)

If the Eq. (56) is written instead of the square of the period and the Eq. (57) as known from the structure dynamics is written instead of the design spectral acceleration value, Eq. (58) is obtained.

$$ T_{1}^{2} = \frac{{4\pi^{2} }}{{\omega^{2} }} $$
(56)
$$ S_{a1} = S_{d1} \omega^{2} $$
(57)
$$ A = \frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }} $$
(58)

Maximum displacement is calculated by the equation below with the help of Eqs. (45), (46), (47) and (58).

$$ \begin{aligned} y\left( 1 \right) & = \frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\left[ {\frac{{\frac{1}{{k^{2} }} - \left[ {\frac{1}{{k^{3} }} - \frac{1}{2k}} \right]\sin \left( k \right)}}{{k^{2} \cos \left( k \right)}}\left] \right[1 - \cosh \left( k \right)} \right] \\ & \quad + \frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\left[ {\frac{1}{{k^{4} }} - \frac{1}{{2k^{2} }}} \right]\left[ {1 - \frac{1}{k}\sinh \left( k \right)} \right] - \frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\frac{1}{{6k^{2} }} \\ \end{aligned} $$
(59)

Equation (59) can be written as below.

$$ y\left( 1 \right) = \nu \left( {k^{2} } \right)S_{d1} $$
(60)

In Eq. (60), the change in ν values according to k2 is given in Table 9.

Table 9 Displacement coefficient for the equivalent static loads method
Full size table

Using the displacement function in Eq. (45), IDR is found as below.

$$ \frac{1}{H}\frac{{dy\left(\upvarepsilon \right)}}{{d\upvarepsilon }} = - \frac{1}{H }S_{1} \left[ {k\sinh \left( {k\upvarepsilon } \right)} \right] + S_{2} \frac{1}{H}\left[ {1 - \cosh \left( {k\upvarepsilon } \right)} \right] - A\frac{{\upvarepsilon ^{2} }}{{2Hk^{2} }} $$
(61)

If the derivation of the function is taken to find the location where the IDRs are maximum in Eq. (61), Eq. (62) is obtained.

$$ \frac{1}{{H^{2} }}\frac{{d^{2} y\left(\upvarepsilon \right)}}{{d\upvarepsilon ^{2} }} = - \frac{1}{{H^{2} }}S_{1} \left[ {k^{2} \cosh \left( {k\upvarepsilon } \right)} \right] + S_{2} \frac{1}{{H^{2} }}\left[ { - k\sinh \left( {k\upvarepsilon } \right)} \right] - A\frac{\upvarepsilon }{{H^{2} k^{2} }} $$
(62)

Ɛ values that make the Eq. (62) zero, show where the IDR is maximum. These Ɛ values are calculated by Eq. (62) for different k values and given in Table 10.

Table 10 Location of the maximum IDR for equivalent static loads method
Full size table

By using Eqs. (46), (47) and (58) in Eqs. (61), (63) is obtained.

$$ \begin{aligned} \frac{1}{H}\frac{{dy\left(\upvarepsilon \right)}}{{d\upvarepsilon }} & = - \frac{1}{H }\frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\left[ {\frac{{\frac{1}{{k^{2} }} - \left[ {\frac{1}{{k^{3} }} - \frac{1}{2k}} \right]\sin \left( k \right)}}{{k^{2} \cos \left( k \right)}}} \right]\left[ {k\sinh \left( {k\upvarepsilon } \right)} \right] \\ & \quad + \frac{1}{H}\frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\left[ {\frac{1}{{k^{4} }} - \frac{1}{{2k^{2} }}} \right]\left[ {1 - \cosh \left( {k\upvarepsilon } \right)} \right] - \frac{{8\pi^{2} S_{d1} }}{{Z_{1}^{2} }}\frac{{\upvarepsilon ^{2} }}{{2Hk^{2} }} \\ \end{aligned} $$
(63)

If Ɛ = Ɛmax is written in Eq. (63), the maximum IDR can be obtained as below.

$$ \frac{1}{H}\frac{{dy\left(\upvarepsilon \right)}}{{d\upvarepsilon }} = \frac{{\upeta \left( {k^{2} } \right)S_{d1} }}{H} $$
(64)

The η values given in Eq. (64) are calculated and presented in Table 11 depending on k2

Table 11 Coefficient of the maximum IDR for the equivalent static loads method
Full size table

4 Contribution of the Axial Deformation

In the presented method, the effect of axial deformations can be approximately taken into account with the approach known from the literature [12]. To this end, KSa is written instead of KS and it is calculated by the following equation [12].

$$ K_{sa} = rK_{s} $$
(65)

Here, r is correction coefficient and it is found with the help of the equation below.

$$ r = \frac{{T_{s1}^{2} }}{{T_{s1}^{2} + T_{a1}^{2} }} $$
(66)
$$ T_{s1}^{2} = 16H^{2} \frac{m}{{hK_{s} }} $$
(67)
$$ T_{a1}^{2} = 3.195H^{4} \frac{m}{hD} $$
(68)

D is the global axial stiffness and it is calculated using the following equation.

$$ D = E\mathop \sum \limits_{i = 1}^{p} A_{ci} t_{i}^{2} $$
(69)

Aci is the plan area of the i-th column, ti shows the distance of the column to the center of gravity in the plan.

5 Numerical Examples

In order to investigate the convergence of the presented method to the Finite Element Method, two examples were solved by the presented method and the results were compared with ETABS.

One of the examples was a 7-storey reinforced concrete structure consist of frames, whereas the second example was a reinforced concrete structure having 15-storey shear wall-frame system.

5.1 Example 1

7-storey reinforced concrete structure of which the bearing system consists of frames, given in Fig. 4 was analyzed by using the presented method in this study. For this purpose, both the Equivalent Static Loads Method and Response Spectrum Analysis were applied to the example. The results obtained by the presented method were compared with the ones obtained by ETABS.

Fig. 4
A layout of the 7-story structure with 6 columns and 6 rows of frames. The dimension between the frames is 4.

Plan of the frame system

Full size image

The height of each storey was 3 m. All columns were 45 cm/45 cm, beams were 25 cm/50 cm and the modulus of the elasticity is 32,000 Mpa. The mass of the storeys were taken as 748,800 kg. The structure was considered in the second seismic zone, local site class Z3 and the seismic load reduction factor was eight for the analysis according to Turkish Earthquake Code.

The comparisons of the presented method and ETABS for the values of maximum displacement and the maximum IDR obtained for the Equivalent Static Loads Method were given in Table 12.

Table 12 The values of maximum displacement and the maximum IDR obtained for the equivalent static loads method (Example 1)
Full size table

As shown in Table 12, the ratio of the maximum difference between the proposed method and ETABS is 9.52%

The comparisons of the presented method and ETABS for the values of maximum displacement and the maximum IDR obtained for the Response Spectrum Analysis were given in Table 13.

Table 13 The values of maximum displacement and the maximum IDR obtained for the Response Spectrum Analysis (Example 1)
Full size table

As it is seen in Table 13, the maximum error according to the solutions by the Response Spectrum Analysis is 5.45%.

5.2 Example 2

15-storey reinforced concrete shear wall-frame structure seen in Fig. 5 was analyzed for the y direction by performing both the Equivalent Static Loads Method and the Response Spectrum Method. The results of the presented method and ETABS were compared.

Fig. 5
A layout of the 7-story structure with 6 columns and 6 rows of frames. The distance between the frames is 4, and the static load is indicated by a dark shaded line between the frames.

Plan of the shear wall frame system

Full size image

The height of each storey was 3 m, columns were 65 cm/65 cm and beams were 30 cm/60 cm, thickness of the shear wall, which was modeled by shell elements in ETABS was 50 cm. The modulus of the elasticity was 33,000 Mpa and the mass of the storeys were taken as 760,000 kg. The structure was considered in the second seismic zone, local site class Z3 and the seismic load reduction factor was six for the analysis according to Turkish Earthquake Code.

The comparison of the first three periods calculated for the structure was given in Table 14.

Table 14 Comparison of natural vibration periods for the first three modes (Example 2)
Full size table

The comparison of the maximum displacement and the maximum IDR for Equivalent Static Loads Method was given in the Table 15.

Table 15 The values of maximum displacement and the maximum IDR obtained for the equivalent static loads method (Example 2)
Full size table

It was seen that, in the analyzes made, both by the presented method and by ETABS the maximum IDR was occurred on the 8th floor level.

The maximum error in the results obtained by the Equivalent Static Loads Method was %8.74.

The comparisons of the maximum displacement and the maximum IDR results of two method obtained by the Response Spectrum Analysis were given in Table 16.

Table 16 The values of maximum displacement and the maximum IDR obtained for Response Spectrum Analysis (Example 2)
Full size table

The maximum error in the results obtained by the Response Equivalent Static Loads Method was %9.16. Maximum IDR was occurred on the 8th floor level by the analysis made by the presented method and by ETABS.

6 Conclusions

In this study, a method to determine the maximum displacement and the maximum interstory drift ratios by using tables has been proposed for the static and dynamic analysis of regular reinforced structures. By the method results of the analyses easily and quickly achieved. It has been observed that the Presented Method gave sufficient results with the Finite Element Method considering the examples that were solved at the end of the study. The approximation of the method is due to the approximation of the determination of the shear stiffness equation and the approximation of the axial deformations. Consequently, the proposed method can be used during the preliminary stage. Also, the method gives an idea about the behavior of the structure.