Autonomous Descent Guidance via Sequential Pseudospectral Convex Programming

Abstract

This chapter expands our development of an autonomous descent guidance algorithm which is able to deal with both the aerodynamic descent and the powered landing phases of a reusable rocket. The method uses sequential convex optimization applied to a Cartesian representation of the equations of motion, and the transcription is based on the use of hp pseudospectral methods. The major contributions of the formulation are a more systematic exploitation and separation of convex and non-convex contributions to minimize the computation of the latter, the inclusion of highly nonlinear terms represented by aerodynamic accelerations, a complete reformulation of the problem based on the use of Euler angle rates as control means, an improved transcription based on the use of a generalized hp pseudospectral method, and a dedicated formulation of the aerodynamic guidance problem for reusable rockets. The approach is demonstrated for a 40 kN-class reusable rocket. Numerical results confirm that the methodology we propose is very effective and able to satisfy all the constraints acting on the system. It is therefore a valid candidate solution to solve the entire descent phase of reusable rockets in real-time.

5.1 Introduction

The last ten years have been disruptive for rocket technology. We are witnessing a paradigm shift which has its focus on reusability, a dream pursued since the beginning of the Space Shuttle program [8], but that only now we are able to fully see as weekly-based, operative technology. This is mainly the result of SpaceX efforts. The company led by Elon Musk paved the way for a deep reshaping of the conception of rockets, mainly with their Falcon 9 program, able, at the moment that this chapter is getting written, to successfully complete its 100th landing [25]. The concurrent development of the even more ambitious Starship program [26], together with the efforts of other players, such as Rocket Lab with its Neutron [9] and Blue Origin with the New Glenn rocket [16] confirms that the disruption we are experiencing is irreversible, and needs to be embraced rather than feared. With this spirit agencies and intergovernmental institutions are updating their plans to keep the pace of the private sector.

In this complex scenario the German Aerospace Center (DLR), the Japan Aerospace Exploration Agency (JAXA), and the French National Centre for Space Studies (CNES) decided to join their resources and know-how in a trilateral agreement aiming at developing and demonstrating the technologies that will be needed for future reusable launch vehicles. The agreement led to the CALLISTO project (Cooperative Action Leading to Launcher Innovation in Stage Toss back Operations) [7], whose demonstrator is currently in development. Its objective is to develop and improve all the critical technologies that are required for making reusable launch systems operative at industrial level in the next decade. The CALLISTO project will culminate in a series of flights that will performed from the Kourou Space Center (KSC), in French Guiana.

To maximize the know-how return of each partner it was decided to have two parallel lines of development for the Guidance and Control (G &C) subsystem. One will be developed by CNES, whereas DLR and JAXA decided to strengthen their efforts and develop a unique, fully integrated G &C solution [23]. Since the focus is to demonstrate reusability technologies for an end-to-end scenario the mission profile consists of multiple flight phases, corresponding to different aerodynamic configurations of the vehicle and different actuation capabilities. Specifically, we identify four main phases of flight, which correspond to different G &C strategies: the ascent phase, the boostback maneuver, the aerodynamic phase, and the powered descent and landing phase. Consequently, several algorithms are required to cope with each of the phases to be able to successfully and autonomously complete such an ambitious mission.

This chapter focuses on the guidance strategy applicable to the last two phases, namely the aerodynamic descent phase and the powered landing phase. As a matter of fact it is well-known that the non-powered, aerodynamically guided phase is critical for the error management in terms of position and velocity [3]. Moreover, large uncertainties due to both the atmosphere and the aerodynamic properties of the vehicle affect the resulting trajectory. Lastly, there will be errors coming from previous segments of flight that the G &C subsystem has to compensate for. All these aspects make the aerodynamic guidance a challenging problem, which requires the capability to generate valid solutions rapidly, in reliable way, and in case significant off-nominal conditions are experienced during the mission, these need be taken into account. On the other hand the powered landing phase requires high accuracy and a perfect coordination of thrust, position, velocity and attitude to meet the strict requirements allowing for a safe and accurate touchdown, the so-called pinpoint landing [4].

Given the aforementioned reasons, the problem of generating valid guidance solutions in the frame of Entry, Descent, and Landing (EDL) has gained great attention, and multiple research groups and companies have worked on the subject. In many different solutions the key technology is represented by the use of Convex Optimization [6], a sub-branch of Numerical Optimization characterized by several intriguing properties, including the guarantee to find a solution if there exists one, a limited dependency on initial guesses, and the computation rapidness, due to state-of-the-art interior point primal-dual solvers [2]. In the specific frame of EDL large attention was dedicated to the application of Second-Order Conic Programming (SOCP), a specific subset of convex optimization, in which all the inequality constraints are formulated in linear or conic form.

Among the proposed methodologies a break-through was represented by the formulation of the entry problem in the energy domain [11]. In this case the non-convex constraints were transformed into upper and lower bounds on the altitude, by expressing the speed as a function of the energy. Moreover, to overcome the non-convexity intrinsically associated with the bank angle $\sigma$, two new controls, defined as the sine and the cosine of the bank angle, were adopted. The substitution was then made valid by ensuring that the identity $\sin {\sigma }^2 +\cos {\sigma }^2 = 1$ was satisfied. Moreover, this formulation overcomes the difficulties of having free-final time, since the final value of energy is automatically obtained by the corresponding final altitude and speed. With the idea of retrieving the benefits of the Space Shuttle Entry Guidance, and generalizing it through the use of convex-optimization technologies, a drag-energy approach based on the application of pseudospectral methods was proposed [22]. In this case a valid drag-energy profile was computed by reformulating the problem in terms of inverse of drag acceleration, and the solution was mapped against longitudinal states to obtain a complete guidance solution. An interesting approach was also formulated by Wang and Grant by exploiting second-order conic programming [29]. In this case the problem was directly transcribed in the time domain by using a direct linearization approach of the nonlinear equations underlying the problem. Wang and Lu further improved the method [30] by means of line-search and trust region techniques that were introduced to speed up the convergence process. The previous approaches were mainly applied to VTHL (Vertical Take-off, Horizontal Landing) vehicles.

For what regards VTVL (Vertical Take-off, Vertical Landing) rockets, the landing phase was extensively treated in the last years, starting from the seminal work of Acikmese et al. [1], and this research area is still very active now, with multiple applications of Convex Optimization [4], Successive Convex Optimization [27, 28], and Pseudospectral Convex Optimization in its standard and generalized forms [18, 20, 21]. Moreover, a first, successful attempt to combine aerodynamic and propulsive control was also proposed by Xinfu Liu [10], where the problem was reduced to two dimensions, and a new set of variables, needed to convexify the subproblem, was introduced. Yang and Liu also proposed to use altitude as independent variable to be able to deal with free-final time powered descent problems [31], through the corresponding manipulation of the equations of motion.

As pointed out by the authors in this last work the methods to deal with non-convex approach through convex techniques can be mainly divided into Direct Linearization Approach and Nonlinearity-Kept and Linearization Approach. In the former the equations of motion, as well as the constraints and the cost function are directly obtained by linearizing the problem around the solution found at the previous iteration. The validity of the approach is ensured by an ad-hoc choice of the static trust regions radii. For this class of methods a drawback can be a slow convergence, and further strategies might be needed to improve the quality of the process [30]. Note that in these approaches the authors introduce some variable transformations aiming at convexifying the problem while keeping nonlinear features of the original formulation. The difficulties in this case arise because of the peculiarity of the transformations needed (which strongly depend on the nature of the problem), the assumptions required to ensure that some simplifications and transformations are valid, and the difficulty to generalize the method (for example it can be hard to extend to the 3-D case the transformations obtained for the in-plane scenario).

In this work we propose a third approach, meant as middle-ground between the two aforementioned techniques. There are four main novelties associated with this work. First, we endorse an ad-hoc formulation of the equations of motion which minimizes the presence of non-convex terms. For example, by using Cartesian representation for position and velocity we avoid the trigonometric terms appearing in the equations of motion for longitude and latitude, which are typically used for aerodynamic entry trajectories [15]. Second, we introduce a different parametrization of controls, based on Euler-angle rates defined with respect to the target-centered Altitude-Crossrange-Downrange directions, in addition to the thrust-rate already adopted in literature. This choice allows to maximize the presence of linear terms in our differential equations while having the controls appearing in affine form, a property which simplifies the convergence process, as pointed out by Liu et al. [12]. Moreover the proposed approach gives us the chance to explicitly limit control rates as well, leading to smooth solutions, and therefore to trajectories which can be more easily tracked by the attitude controller.

The third novelty relies on entirely convoying the nonlinearities into the terms appearing in the differential equations representing the accelerations for the aerodynamic phase and the mass rate. We consequently apply numerical linearization only to these terms, obtaining therefore an hybrid computation of the matrix representing the equation of motion in linearized form.

The fourth aspect we want to emphasize is the use of a systematic transcription based on generalized hp pseudospectral methods, already adopted for the powered landing problem [20], but here extended to deal with the aerodynamic phase problem too. This choice benefits from the properties of pseudospectral methods [19], such as the quasi-exponential (or spectral) convergence, and the easiness of implementation. Moreover, its mapping between time and pseudotime is conveniently exploited to formulate the free-final time problem, leading to an increased capability of handling initial dispersions, since we don’t need any accurate a-priori knowledge or estimate of the flight time for off-nominal cases.

A last remark concerns the non-convex accelerations, with special focus on the aerodynamic terms: it is in fact worth mentioning that in related works some simplifications (e.g., constant drag coefficient) are typically made, given their relative importance. However, in this work we focus on conditions which are as close as possible to what the vehicle in a real scenario will experience. Therefore we reject these simplifications typically used for this class of methods, (e.g., constant gravity, negligible lift, or constant drag coefficient). Instead, we use a full-blown aerodynamic database, which includes lift, drag, side-force, as well as aerodynamic torques, which depend on the 3-D attitude of the vehicle as well as on the Mach number [14]. These assumptions are required given the centrality of the aerodynamic accelerations for this type of problems.

Numerical results are shown for a CALLISTO-class rocket. We extend our recent results [21] by also analyzing off-nominal conditions for both the flight phases. The chapter is organized as follows: in Sect. 5.2 the mission and the vehicle are briefly described, while Sect. 5.3 focuses on the problem formulation in continuous form. Sections 5.4 and 5.5 describe the convexified approach and its corresponding pseudospectral transcription, respectively, while numerical results are described in Sect. 5.6. Finally, we draw some conclusions in Sect. 5.7.

5.2 Mission and Vehicle

In this section we provide an overview of the mission scenario as well as of the vehicle.

5.2.1 Vehicle and Mission Overview

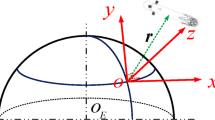
As mentioned in the introduction the vehicle considered in this work is a 40-kN class rocket. The rocket thrust can be throttled between 40 and 110% of its nominal maximum value, and the engine is mounted on a gimballed system able to provide pitch and yaw control capability during the powered phases, namely ascent and landing. Roll control is ensured by a set of eight reaction control system (RCS) thrusters, mounted on top of the rocket. During the unpowered phases we can rely on a set of four steerable fins mounted on top. They are able to provide complete aerodynamic control, ensuring full control throughout the entire mission. An impression of the rocket used as example for this work is depicted in Fig. 5.1. The mission considered is a Return To Launch Site (RTLS) Scenario. This means that the rocket will fly back and perform the landing onto a platform that is very close to the launch site, as visible in Fig. 5.1. A series of flights will take place at the Guiana Space Center, the European Spaceport in French Guiana. This flight campaign will give indications on the level of refurbishment required between two consecutive flights performed with the same vehicle, while providing first-hand data to all the partners to further enhance the knowledge of reusable technologies and some of the related critical technologies, especially in terms of Guidance, Navigation and Control domain.

Fig. 5.1

Mission and vehicle overview: a CALLISTO rocket, b Reference mission profile

5.2.2 Rocket Modeling

While mass and center of mass (CoM) are considered constant during the aerodynamic descent, during the powered phase the vehicle experiences a significant variation of both these variables. This effect is accounted for by storing the CoM as a lookup-table depending on the current mass. Mass variations coming from RCS are in this context neglected. Therefore, we can express this dependency as

$$\begin{aligned} CoM = CoM(m) \end{aligned}$$

(5.1)

Fig. 5.2

Vertical and horizontal angles of attack

The axis-symmetry of the vehicle has been exploited to compute aerodynamic coefficients as function of an horizontal and a vertical angle of attack $\alpha _1$ and $\alpha _2$, as illustrated in Fig. 5.2. The aerodynamic force coefficients with respect to the body axes

$$\begin{aligned} \textbf{C}^{aero}_{BODY} = [C^{aero}_{BODY,x}C^{aero}_{BODY,y}C^{aero}_{BODY,z}]^T \end{aligned}$$

are provided as multidimensional look-up tables, which depend on Mach number M, and angles of attack $\alpha _1$ and $\alpha _2$, and on the four fin deflections $\delta _1$,$\delta _2$,$\delta _3$,$\delta _4$.

$$\begin{aligned} \textbf{C}^{aero}_{BODY} = \left[ \begin{array}{c} C^{aero}_{BODY,x}(M,\alpha _1,\alpha _2,\delta _1,\delta _2,\delta _3,\delta _4) \\ C^{aero}_{BODY,y}(M,\alpha _1,\alpha _2,\delta _1,\delta _2,\delta _3,\delta _4) \\ C^{aero}_{BODY,z}(M,\alpha _1,\alpha _2,\delta _1,\delta _2,\delta _3,\delta _4) \\ \end{array} \right] \end{aligned}$$

(5.2)

From these coefficients the aerodynamic force can be computed as

$$\begin{aligned} \begin{array}{cc} \textbf{F}^{aero}_{BODY,i} = \frac{1}{2}\rho V^2\,S \textbf{C}^{aero}_{BODY,i}&,\quad i = x,y,z \end{array} \end{aligned}$$

(5.3)

with the reference surface S equal to 0.95 m. The term $\rho$ represents the atmospheric density, which depends on altitude, whereas V is the speed of the vehicle with respect to the air. For what regards the atmospheric density we employ a model coming from experimental measures, and provided as look-up table, where the geodetic altitude is the independent variable.

$$\begin{aligned} \rho = \rho (h) \end{aligned}$$

This choice confirms once more that no strong simplifications (i.e., exponential atmospheric profile) are required with the proposed method.

Remark 1: Note that, although this solution is inherently based on a 3-DOF model we are interested to generate solutions which we define 6-DOF capable, which means the generated trajectory has to provide an attitude which can be trimmed by the aerodynamic fins. This aspect is currently included in the present work, as it will be shown in Sect. 5.6.

5.3 Problem Formulation

In this section we describe in detail the problem formulation for both the aerodynamic descent and the powered landing phases of the flight.

Aerodynamic Descent

A. Equations of Motion

We describe the aerodynamic guidance problem in a target-centered Downrange-Crossrange-Altitude (DCA) reference frame, as depicted in Fig. 5.1. This reference frame can be thought of as a Up-East-North local reference frame rotated around the x-axis to align the z-axis with the plane containing most of the trajectory. We cannot rely on thrust during this phase, and therefore only the aerodynamic forces can be used to control the vehicle. These forces are a direct function of the speed and the relative attitude of the body axes with respect to the airflow. Therefore the attitude is implicitly the main way to control the rocket, modeled in this work as a 3-DOF point mass. The desired attitude will then define the reference signals to be tracked by the attitude controller, which is realized by using the fins to generate the desired aerodynamic torques. The translational dynamics equations can be described as follows. Note that from now on the reference frame indication is omitted for brevity.

$$\begin{aligned} \begin{array}{c} \dot{\textbf{r}} = \textbf{v}\\ \dot{\textbf{v}} = \textbf{a}^{grav} + \textbf{a}^{aero} - 2 \omega \times \textbf{v} - \omega \times \left( \omega \times \textbf{r}\right) \\ \dot{\theta } = u_\theta \\ \dot{\psi } = u_\psi \end{array} \end{aligned}$$

(5.4)

The terms $\textbf{r}$ and $\textbf{v}$ are the position and the velocity of the CoM of the vehicle expressed in the DCA reference frame. We include non-inertial terms due to the rotation of the Earth $\omega$, whereas $\theta$ and $\psi$ are the pitch and yaw angle of the rocket with respect to the target-centered Downrange-Crossrange-Altitude reference frame. We assume that the roll angle is kept constant during the descent to maximize the decoupling between pitch and yaw axes. Note that the controls we effectively use are the pitch rate $u_\theta$ and the yaw rate $u_\psi$. This choice is twofold beneficial: first, it decouples the control matrix from the states, as we will see. Second, it allows to impose explicit bounds on the control rates, making the solution smoother. The sources of non-convexity are in this case two: the gravity, which is a non-linear function of position, and the aerodynamic accelerations, which depend nonlinearly on altitude, velocity, and attitude angles. For what regards the gravity we can assume a central-body model,

$$\begin{aligned} \textbf{a}^{grav} = -\mu _{\oplus }\frac{\textbf{r}+\textbf{r}_{T}}{\left\| \textbf{r}+\textbf{r}_{T} \right\| ^3_2} \end{aligned}$$

(5.5)

with $\mu _{\oplus }$ representing the gravitational parameter of the Earth, while $\textbf{r}_T$ is the position vector of the target site with respect to the center of the Earth. Note that with this formulation more accurate models, like the one based on the World Geodetic System 84, could be adopted. However, this more advanced modeling is kept for future development, and a simpler choice was here preferred. For what regards the aerodynamic accelerations they represent a nonlinear combination of the states. In fact, the aerodynamic accelerations are, for the rocket under analysis, expressed in body-reference frame as

$$\begin{aligned} \textbf{a}^{aero}_{BODY} = \frac{1}{m}\textbf{F}^{aero}_{BODY}(\alpha _1,\alpha _2,M,q_{dyn},\delta _1,\dots ,\delta _4) \end{aligned}$$

(5.6)

where $\alpha _1$ and $\alpha _2$ are the vertical and horizontal angle of attack (introduced in Fig. 5.2 and used to exploit the axis-symmetry of the vehicle) M represents the Mach number, while $q_{dyn}$ is the dynamic pressure, function of the altitude (through the atmospheric density $\rho$) and the speed V.

$$\begin{aligned} q_{dyn} = \frac{1}{2}\rho V^2 \end{aligned}$$

(5.7)

Since we are interested to express the aerodynamic accelerations in DCA coordinates it is necessary to transform the outcome of Eq. (5.6) as

$$\begin{aligned} \textbf{a}^{aero}_{DCA} = \textbf{R}_{BODY}^{DCA} \cdot \textbf{a}^{aero}_{BODY} \end{aligned}$$

(5.8)

where $\textbf{R}_{BODY}^{DCA}$ represents the rotation matrix from BODY to DCA. This matrix is composed by two different contributions.

$$\begin{aligned} \textbf{R}_{BODY}^{DCA} = \textbf{R}_{UEN}^{DCA} \cdot \textbf{R}_{BODY}^{UEN} \end{aligned}$$

(5.9)

with UEN representing the target-fixed Up-East-North reference frame. Note that the first term of the right hand side of Eq. (5.9) is only function of the target position $\textbf{r}_{T}$ and of the angle $\chi$ identifying the trajectory plane. Both are constant,

$$\begin{aligned} \textbf{R}_{UEN}^{DCA} = \textbf{R}_{UEN}^{DCA}(\textbf{r}_{T},\chi ) \end{aligned}$$

(5.10)

while the second contribution is a direct function of the attitude of the body. In fact, we can write

$$\begin{aligned} \textbf{R}_{BODY}^{UEN} = \textbf{R}_{BODY}^{UEN}(\theta ,\psi ) \end{aligned}$$

(5.11)

and this relationship embeds part of the nonlinearities requiring linearization. Note that the derivation of the aerodynamic accelerations in DCA is not only necessary for the formulation of the equations of motion, but is also useful because it gives us an indication of the dependencies to be considered when the linearized equations of motion are derived.

B. Boundary Conditions

The problem will have fixed initial and final conditions, coming from previous and successive phases of flight,

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} \textbf{r}_{DCA}(t_0) \\ \textbf{v}_{DCA}(t_0) \\ \mathbf {\theta }_{DCA}(t_0)\\ \mathbf {\psi }_{DCA}(t_0)\\ \textbf{r}_{DCA}(t_F) \\ \textbf{v}_{DCA}(t_F) \\ \mathbf {\theta }_{DCA}(t_F)\\ \mathbf {\psi }_{DCA}(t_F) \end{array} \right] &{} = &{} \left[ \begin{array}{c} \textbf{r}_{DCA,0}\\ \textbf{v}_{DCA,0}\\ {\theta }_{DCA,0}\\ {\psi }_{DCA,0}\\ \textbf{r}_{DCA,F}\\ \textbf{v}_{DCA,F}\\ {\theta }_{DCA,F}\\ {\psi }_{DCA,F} \end{array} \right] \end{array} \end{aligned}$$

(5.12)

as we want, at the end of the aerodynamic descent (occurring at the free final time $t_F$) to be in conditions of correctly switching to the powered phase in optimal conditions for the pinpoint landing.

Remark 2: Note that the Euler angles adopted throughout this work are built on the Up-East-North convention, and not on the traditional North-East-Down. This choice is motivated by the need to avoid the classical singularity of the pitch angle at 90$^\circ$, which is what would happen for a vertical descending vehicle. With the adopted convention we ensure to be away from the singularity, as the vertical descent is associated with a pitch angle $\theta = 0^\circ$.

C. Constraints

For the aerodynamic phase no nonlinear constraints were taken into account in this specific example, even though it is possible to do it by directly linearizing them ([21, 29]).

D. States and controls bounds

Finally, we want to have a meaningful upper bound and lower bound on the states,

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} {r_x}_{L} \\ {r_y}_L \\ {r_z}_L \\ {v_x}_L \\ {v_y}_L \\ {v_z}_L \\ {\theta }_L \\ {\psi }_L \end{array} \right] \le &{} \left[ \begin{array}{c} {r_x} \\ {r_y} \\ {r_z} \\ {v_x} \\ {v_y} \\ {v_z} \\ {\theta } \\ {\psi } \end{array} \right] \le &{} \left[ \begin{array}{c} {r_x}_{U} \\ {r_y}_U \\ {r_z}_U \\ {v_x}_U \\ {v_y}_U \\ {v_z}_U \\ {\theta }_U \\ {\psi }_U \end{array} \right] \end{array} \end{aligned}$$

(5.13)

which derive mainly from flight-safety studies. Moreover, to limit the closed-loop bandwidth associated with the attitude controller, and generate a smooth solution, upper and lower bounds are also assigned to the rates of pitch and yaw angles, with $u_{\theta ,max} = u_{\psi ,max} = 10^\circ$/s.

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} -u_{\theta ,max} \\ -u_{\psi ,max} \end{array} \right] \le &{} \left[ \begin{array}{c} u_\theta \\ u_{\psi } \end{array} \right] \le &{} \left[ \begin{array}{c} u_{\theta ,max} \\ u_{\psi ,max} \end{array} \right] \end{array} \end{aligned}$$

(5.14)

E. Cost function

Finally, for this problem we are interested to minimize the control activity, therefore we simply express the cost function as

$$\begin{aligned} J = \int _{t_0}^{t_F}\left[ u_\theta ^2(t)+u_\psi ^2(t)\right] dt \end{aligned}$$

(5.15)

where Eq. (5.15) will be weighted by a user-defined positive weight $w_u$, whose value is formally irrelevant here, but becomes important in the construction of an augmented cost function that takes also other effects into account, as it will be shown in Sects. 5.4 and 5.5. The problem to be solved is therefore the following: we aim at minimizing Eq. (5.15) with the system subject to the differential equations defined in Eq. (5.4). The solution has to satisfy the boundary conditions given by Eq. (5.12), as well as states and control box constraints defined according to Eqs. (5.13) and (5.14).

Powered Landing

A. Equations of motion

We can extend the previous formulation to the powered landing problem. Several elegant formulations have been proposed over the years to deal with this problem. Here we aim at including the presence of realistic effects, which in order of relevance are (1) the thrust-aerodynamic forces interaction, (2) the minimization of aerodynamic torques that could prevent the 6-DOF feasibility of the trajectory, (3) the motion of the center of mass while descending, (4) the effect of the pressure on the effective thrust generated, and 5) other effects, like non-constant gravitational acceleration and non-inertial forces due to the rotation of the Earth. While in the previous subsection we were using the aerodynamic forces as means of control in this case their effect is combined with the force exerted by the engine to dominate the motion of the rocket. The corresponding model is a 3-DOF point having variable mass, and its evolution is described by the following set of equations:

$$\begin{aligned} \begin{array}{c} \dot{\textbf{r}} = \textbf{v}\\ \dot{\textbf{v}} = \textbf{a}^{thr} + \textbf{a}^{grav} + \textbf{a}^{aero} - 2 \omega \times \textbf{v} - \omega \times \left( \omega \times \textbf{r}\right) \\ \dot{m} = -\frac{T_{vac}}{I_{sp}g_0}\\ \dot{\phi } = u_\phi \\ \dot{\theta } = u_\theta \\ \dot{\psi } = u_\psi \\ \dot{T}_{atmo} = u_T \end{array} \end{aligned}$$

(5.16)

Note the presence of the roll angle $\phi$, the mass m and the atmospheric thrust $T_{atmo}$, with the last two terms linked to the vacuum thrust $T_{vac}$ through the equation

$$\begin{aligned} T_{atmo} = T_{vac} - A_{nz}p \end{aligned}$$

(5.17)

with $A_{nz}$ indicating the nozzle area, p the atmospheric pressure, and $T_{vac}$ the thrust generated in vacuum. The controls are for this scenario the Euler angle rates $u_\phi$, $u_\theta$, $u_\psi$. Moreover, to limit the instantaneous change of thrust, not compatible with the physical rocket engine, we include the thrust rate $u_T$. This choice gives the chance to decouple the control matrix from the states as done for the aerodynamic descent, and at the same time to obtain solution physically realizable by the rocket’s actuators. For this problem there are four different sources of non-convexity: in addition to the aforementioned gravity and aerodynamic accelerations we have now the acceleration caused by the thrust $\textbf{a}_{thr} = \textbf{T}_{atmo}/m$. Moreover, there is an exponential-like dependence on the massflow from the altitude through the pressure in virtue of Eq. (5.17). The aerodynamic accelerations can be computed again by invoking Eq. (5.6) and we can convert them into their DCA representation exactly as done through Eqs. (5.8)–(5.10). The only difference is represented by the modification of Eq. (5.11), which, in virtue of the dependence on the roll angle $\phi$ is re-written as follows.

$$\begin{aligned} \textbf{R}_{BODY}^{UEN} = \textbf{R}_{BODY}^{UEN}(\phi ,\theta ,\psi ) \end{aligned}$$

(5.18)

B. Boundary Conditions

The boundary conditions described in Eqs. (5.12) are still valid. We augment them with some further conditions coming from the new variables included in the problem as follows.

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} m(t_0) \\ \mathbf {\phi }_{DCA}(t_0) \\ T(t_0) \\ \mathbf {\phi }_{DCA}(t_F) \end{array} \right] &{} = &{} \left[ \begin{array}{c} m_{0}\\ {\phi }_{DCA,0}\\ T_{0}\\ {\phi }_{DCA,F} \end{array} \right] \end{array} \end{aligned}$$

(5.19)

Note that we omitted the final value of mass and thrust, as they are determined by the algorithm. Moreover, we include final conditions for the attitude to ensure that the vehicle lands with its x-body axis being normal to the local horizontal plane.

C. Constraints

Three types of constraints are included here: first, we introduce the classical glideslope constraint to enforce the vehicle to impose a controlled ratio between reduction of horizontal and vertical distance with respect to the landing spot.

$$\begin{aligned} \frac{r_A}{\left\| \textbf{r}_{D,C} \right\| }\ge \tan {\gamma _{gs}} \end{aligned}$$

(5.20)

with glideslope angle equal to 70$^\circ$. To further enforce a vertical motion towards the end of the pinpoint landing sequence it is imposed that in the last segment of the trajectory, approximately corresponding to the last 5 s of flight, both side-components of position and velocity are bounded, and specifically

$$\begin{aligned} \begin{array}{c} \left\| \textbf{r}_{D,C}(t\le t_F-t^*) \right\| \le r_{D,C,max}\\ \left\| \textbf{v}_{D,C}(t\le t_F-t^*) \right\| \le v_{D,C,max}\\ \end{array} \end{aligned}$$

(5.21)

with $t^*$ equal to 5 s, $r_{D,C,max}$ equal to 1 m, and $v_{D,C,max}$ defined as 0.1 m/s.

Note that all these constraints can be modeled as second-order conic constraints, and therefore do not require linearization.

D. States and controls bounds

While Eqs. (5.13)–(5.14) still hold for the powered phase too, we augment them according to the problem definition by adding the following box constraints for the states,

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} m_L\\ {\phi }_L \\ T_L \end{array} \right] \le &{} \left[ \begin{array}{c} m \\ \phi \\ T \end{array} \right] \le &{} \left[ \begin{array}{c} m_u \\ \phi _U \\ T_U \end{array} \right] \end{array} \end{aligned}$$

(5.22)

and the controls

$$\begin{aligned} \begin{array}{ccc} \left[ \begin{array}{c} -u_{\phi ,max} \\ -u_{T,max} \end{array} \right] \le &{} \left[ \begin{array}{c} u_{\phi } \\ u_T \end{array} \right] \le &{} \left[ \begin{array}{c} u_{\phi ,max} \\ u_{T,max} \end{array} \right] \end{array} \end{aligned}$$

(5.23)

with $u_{\theta ,max} = u_{\psi ,max} = 5^\circ$/s, while the roll rate is limited to 0.1$^\circ$/s. Finally, a maximum throttle rate $u_{T,max}$ here normalized, is included in the formulation. Finally, note that with the current formulation the thrust vector inclination is not constrained, as we are relying on a 3-DoF formulation. However, given the constraint on the final body axes the thrust tilt angle is implicitly constrained to be within $\pm \delta _{TVC,max}$ with respect to the local vertical axes at touchdown, where $\delta _{TVC,max}$ is the maximum thrust gimbal angle.

E. Cost function

The cost function we build for this problem is made of different contributions: first, we are interested to maximize the final mass of the vehicle, which corresponds to the minimization of the fuel required to perform the landing maneuver. Moreover, we introduce a penalization of the control rates to ensure that the solution we obtain is smooth enough.

$$\begin{aligned} J = -w_m m(t_F) + w_u\int _{t_0}^{t_F}\left( \textbf{u}^T\cdot \textbf{R}\cdot \textbf{u} \right) dt \end{aligned}$$

(5.24)

The vector $\textbf{u}$ embeds all the four controls included in the formulation through $\textbf{R}$, defined as a unitary diagonal matrix, while the terms $w_m$ and $w_u$ measure the relative importance of the two terms in the optimization process, with the former not excessively larger than the latter. This choice is motivated by the fact that while we are interested to optimize the fuel consumption, we also want to discourage through the presence of the term $w_u$ large variations of the control rates. In fact, larger control variations could lead to hectic control profiles, which might be slightly more efficient from the fuel-consumption perspective, but less safe. We have therefore completely defined the problem to be solved: we aim at minimizing Eq. (5.24) with the system subject to the differential equations defined in Eq. (5.16). The solution has to satisfy the boundary conditions given by Eqs. (5.12), (5.19) and (5.13)–(5.14), (5.22)–(5.23) as well as the constraints of Eqs. (5.20) and (5.21).

5.4 Convex Formulation

In this section we will transform the two continuous problems described in Sect. 5.3 into a sequence of convex problems, to be solved iteratively.

Aerodynamic Descent

A. Equations of motion

For what regards the equations of motion during the aerodynamic phase we can decompose the system described in Eq. (5.4) in a convex part, and a non-convex part. Defined the state vector as

$$\begin{aligned} \textbf{x} = \left[ \begin{array}{cccc} \textbf{r}_{DCA}&\textbf{v}_{DCA}&\theta&\psi \end{array} \right] ^T \end{aligned}$$

(5.25)

we can write the equations of motion as

$$\begin{aligned} \dot{\mathbf {{x}}} = \textbf{f}_{nc}(\textbf{x})+\textbf{f}_{c}(\textbf{x})+\textbf{B}\textbf{u}+\textbf{C}\mathbf {\nu } \end{aligned}$$

(5.26)

with

$$\begin{aligned} \textbf{u} = \left[ \begin{array}{cc} {u}_{\theta }&{u}_{\psi } \end{array} \right] ^T \end{aligned}$$

(5.27)

representing the physical controls used to manipulate the attitude of the vehicle, and consequently, the aerodynamic forces generated, while the vector $\nu \in \mathbb {R}^{n_s}$, defined as

$$\begin{aligned} \textbf{v} = \left[ \begin{array}{cccccccc} \mathbf {\nu }_{r_x}&\mathbf {\nu }_{r_y}&\mathbf {\nu }_{r_z}&\mathbf {\nu }_{v_x}&\mathbf {\nu }_{v_y}&\mathbf {\nu }_{v_z}&\mathbf {\nu }_{\theta }&\mathbf {\nu }_{\psi } \end{array} \right] ^T \end{aligned}$$

(5.28)

represents the virtual controls, required to avoid artificial infeasibility [28]. The matrix $\textbf{C}$ is a design parameter to decide which and how many virtual controls will be used to help the convergence process. For this work the matrix is defined as

$$\begin{aligned} \textbf{C} = \left[ \begin{array}{cc} \textbf{I}_{6\times 6} &{} \textbf{O}_{6\times 2} \\ \textbf{O}_{2\times 6} &{} \textbf{O}_{2\times 2} \end{array} \right] \end{aligned}$$

(5.29)

which implies that virtual controls are only applied to the translational states, acting as synthetic accelerations and velocities affecting the differential equations of ${\textbf{v}}$ and ${\textbf{r}}$, respectively. This choice is due to the nature of the problem, given that including virtual controls affecting the attitude states might not provide any physical improvement to the convergence process.

For what regards the convex terms, they are represented by

$$\begin{aligned} \textbf{f}_c(\textbf{x}) = \left[ \begin{array}{c} \textbf{v}_{DCA} \\ - 2 \omega \times \textbf{v}_{DCA} - \omega \times \left( \omega \times \textbf{r}_{DCA}\right) \\ \textbf{O}_{2 \times 1} \\ \end{array}\right] = \textbf{A}_c \cdot \textbf{x} \end{aligned}$$

(5.30)

with

$$\begin{aligned} \textbf{A}_c \triangleq \left[ \begin{array}{ccc} \textbf{O}_{[3\times 3]} &{} \textbf{I}_{[3\times 3]} &{} \textbf{O}_{[3 \times 2]} \\ - \omega \times \left( \omega \times \right) &{} - 2 \omega \times &{} \textbf{O}_{[3 \times 2]} \\ \textbf{O}_{[3\times 3]} &{} \textbf{O}_{[3\times 3]} &{} \textbf{O}_{[3\times 2]} \end{array} \right] \end{aligned}$$

(5.31)

The matrix $\textbf{A}_c$ only contains constant terms, and is therefore computed only once during the initialization of the algorithm.

The non-convex term can be convoyed into the fourth, fifth and sixth elements of the vector

$$\begin{aligned} \textbf{f}_{nc}(\textbf{x}) = \left[ \begin{array}{c} \textbf{O}_{3 \times 1} \\ \textbf{a}^{grav}_{DCA} + \textbf{a}^{aero}_{DCA}\\ \textbf{O}_{2 \times 1} \\ \end{array}\right] \end{aligned}$$

(5.32)

and this contribution represents the only term that requires linearization. Finally, the control matrix $\textbf{B}$ is

$$\begin{aligned} \textbf{B} = \left[ \begin{array}{c} \textbf{O}_{6 \times 2} \\ \textbf{I}_{2 \times 2} \end{array}\right] \end{aligned}$$

(5.33)

We can see that the system is affine in control, which is a very important property of the problem to be iteratively solved by using sequential convex programming, as demonstrated by Liu et al. [12]. Moreover, the structure chosen to represent the problem suggests us that we can apply a partial linearization and perform sequential convex programming by exploiting the distinction between convex and non-convex terms. On this purpose, suppose we have solved the problem k times, with $k = 0,\dots , k_{max}$. The solution with $k = 0$ can either be a propagation of dummy controls, or a linear interpolation between initial and final states and controls. To solve the $(k+1)$th sub-problem we linearize the nonlinear terms of equations of motion around the sub-solution k. The subscript k will indicate the terms computed by using the corresponding kth solution. We can therefore rewrite the system described in Eq. (5.26) as

$$\begin{aligned} \dot{\textbf{x}} = \textbf{A}_c \textbf{x} + \textbf{A}_k\textbf{x} + \textbf{B}\textbf{u} + \textbf{C}\mathbf {\nu }+\textbf{G}_k \end{aligned}$$

(5.34)

where

$$\begin{aligned} \textbf{A}_k \triangleq \frac{\partial \textbf{f}_{nc}\left( \textbf{x}\right) }{\partial \textbf{x}}{\Bigg |}_{\textbf{x}=\textbf{x}_{k}} \end{aligned}$$

(5.35)

and

$$\begin{aligned} \textbf{G}_k \triangleq \textbf{f}_{nc}(\textbf{x}_k)-\textbf{A}_k\textbf{x}_k \end{aligned}$$

(5.36)

Note that, as highlighted by multiple authors [28, 30] it is necessary that the new solution does not largely differ from the previous one. This condition is needed to ensure that the nonlinear behavior of the system is well captured by the first two terms of the Taylor expansions underlying the linearization. To have a meaningful linearization process trust-region constraints are adopted. The way to implement trust-region constraints has been widely treated in literature in multiple forms. Some researchers prefer to express the trust-region radius as a user-defined vector [10]. This approach has the advantage to reduce the size of the problem, since the trust-region size is an input to the subproblem to be solved, rather than a variable to be optimized. Other relevant works include update rules for shrinking or enlarging their size depending on some metrics measuring the validity of the linearization at each iteration [5, 13]. Finally, a further approach consists in introducing dynamic upper bounds for the trust region as part of the subproblem formulation [28]. In a similar fashion to this last approach we introduce trust-region upper bounds on the difference between the new solution and the previous iteration, used to build the current subproblem to be solved.

$$\begin{aligned} \left\| {\tilde{\textbf{X}}}(t)-{\tilde{\textbf{X}}}_k(t) \right\| \le \zeta (t) \end{aligned}$$

(5.37)

with

$$\begin{aligned} {\tilde{\textbf{X}}} \triangleq \left[ \begin{array}{c} \textbf{x}(t) \\ \textbf{u}(t) \end{array}\right] , \quad {\tilde{\textbf{X}}}_k \triangleq \left[ \begin{array}{c} \textbf{x}_k(t) \\ \textbf{u}_k(t) \end{array}\right] \end{aligned}$$

(5.38)

and $\zeta$ representing an upper bound that limits the excursion between two consecutive iterations, to be penalized as well through a corresponding slack variable

$$\begin{aligned} \left\| \mathbf \zeta \right\| _2 \le s_\zeta ,\quad s_\zeta \in \mathbb {R} \end{aligned}$$

(5.39)

Note that the problem must be scaled in order to have the construction of the norm in Eq. (5.37) to be a legitimate operation.

B. Constraints

As mentioned in Sect. 5.3 no nonlinear constraints have been considered in the formulation of the aerodynamic guidance problem. However other constraints need to be included: specifically, we define upper and lower bounds on states and controls corresponding to Eqs. (5.13)–(5.14) as pointwise linear inequalities. Moreover, we need to impose constraints on virtual controls. Since they are only used to avoid artificial obstructions, it is required to reduce them to a negligible value along the convergence process to ensure that the computed trajectory is a physical solution to our problem. For this reason, as already proposed in literature ([28]) every virtual control vector is bounded by a corresponding slack variable $\eta _\nu$

$$\begin{aligned} \left\| \mathbf \nu \right\| _2 \le \eta _\nu ,\quad \eta _\nu \in \mathbb {R}^{np} \end{aligned}$$

(5.40)

and to ensure that the virtual controls are minimized over the process, we include a further slack variable as upper bound for the norm of $\eta _\nu$:

$$\begin{aligned} \left\| \mathbf \eta _\nu \right\| _2 \le s_\eta \end{aligned}$$

(5.41)

with the term $s_\eta$ included in the cost function, and scaled by a positive value $w_\eta$.

C. Augmented Cost function

To include the penalization of trust regions and virtual controls in the formulation the augmented cost function for the subproblem is defined as

$$\begin{aligned} J_{aug}(\textbf{x},\textbf{u},\mathbf {\nu },\mathbf {\zeta },s_\eta ,s_\zeta ) = w_u J + w_\eta \cdot s_\eta + w_\zeta \cdot s_\zeta \end{aligned}$$

(5.42)

with the weights $w_\eta$ and $w_\zeta$ measuring the relative importance of the penalization of virtual control and trust region with respect to the true cost function J defined in Eq. (5.15), which is weighted by $w_u$. In this work $w_\eta$ is assumed equal to $10^4$ for both the descent and the landing phases, while $w_\zeta$ is equal to $10^{-1}$ for the aerodynamic phase, and to 1 for the powered segment. This choice gives full priority to the reduction of the virtual controls, and poses as secondary objective the shrinkage of the trust-region radii. A unitary value of $w_u$ is associated with the original cost function. In conclusions during the aerodynamic phase we are interested to optimize at each iteration Eq. (5.42), subject to Eqs. (5.34) while ensuring proper penalization of both the trust region size through Eqs. (5.37) and (5.39), and a shrinkage of virtual controls through Eqs. (5.40) and (5.41).

Powered Landing

A. Equations of motion

By extending the logic of the previous section, we expand the state vector for the powered landing phase in the following manner,

$$\begin{aligned} \textbf{x} = \left[ \begin{array}{ccccccc} \textbf{r}_{DCA}&\textbf{v}_{DCA}&m&\phi&\theta&\psi&T \end{array} \right] ^T \end{aligned}$$

(5.43)

with the corresponding dynamics that in vector-form remains the same as Eq. (5.26) but where the control vector is now the following.

$$\begin{aligned} \textbf{u} = \left[ \begin{array}{cccc} {u}_{\phi }&{u}_{\theta }&{u}_{\psi }&u_T \end{array} \right] ^T \end{aligned}$$

(5.44)

The virtual control vector $\nu \in \mathbb {R}^{n_s}$, is in this case defined as

$$\begin{aligned} \textbf{v} = \left[ \begin{array}{ccccccccccc} \mathbf {\nu }_{r_x}&\mathbf {\nu }_{r_y}&\mathbf {\nu }_{r_z}&\mathbf {\nu }_{v_x}&\mathbf {\nu }_{v_y}&\mathbf {\nu }_{v_z}&\nu _m&\mathbf {\nu }_{\phi }&\mathbf {\nu }_{\theta }&\mathbf {\nu }_{\psi }&\nu _T \end{array} \right] ^T \end{aligned}$$

(5.45)

and the matrix $\textbf{C}$ defined in Eq. (5.29) is augmented accordingly,

$$\begin{aligned} \textbf{C} = \left[ \begin{array}{cc} \textbf{I}_{6\times 6} &{} \textbf{O}_{6\times 5} \\ \textbf{O}_{5\times 6} &{} \textbf{O}_{5\times 5} \end{array} \right] \end{aligned}$$

(5.46)

such that also in this case virtual controls affect the translational motion only. The convex terms are common to those defined during the aerodynamic descent, modified only to take the different size of the state vector into account.

$$\begin{aligned} \textbf{f}_c(\textbf{x}) = \left[ \begin{array}{c} \textbf{v}_{DCA} \\ - 2 \omega \times \textbf{v}_{DCA} - \omega \times \left( \omega \times \textbf{r}_{DCA}\right) \\ \textbf{O}_{5 \times 1} \\ \end{array}\right] = \textbf{A}_c \cdot \textbf{x} \end{aligned}$$

(5.47)

with

$$\begin{aligned} \textbf{A}_c \triangleq \left[ \begin{array}{ccc} \textbf{O}_{[3\times 3]} &{} \textbf{I}_{[3\times 3]} &{} \textbf{O}_{[3 \times 5]} \\ - \omega \times \left( \omega \times \right) &{} - 2 \omega \times &{} \textbf{O}_{[3 \times 5]} \\ \textbf{O}_{[5\times 3]} &{} \textbf{O}_{[5\times 3]} &{} \textbf{O}_{[5\times 5]} \end{array} \right] \end{aligned}$$

(5.48)

The non-convex terms are grouped into the fourth, fifth, sixth and seventh differential equations coming from Eq. (5.16).

$$\begin{aligned} \textbf{f}_{nc}(\textbf{x}) = \left[ \begin{array}{c} \textbf{O}_{3 \times 1} \\ \textbf{a}^{thr}_{DCA} + \textbf{a}^{grav}_{DCA} + \textbf{a}^{aero}_{DCA}\\ -\frac{T_{vac}}{I_{sp}g_0}\\ \textbf{O}_{4 \times 1} \\ \end{array}\right] \end{aligned}$$

(5.49)

As previously done, numerical linearization is applied to these terms only. Finally, the control matrix $\textbf{B}$ is

$$\begin{aligned} \textbf{B} = \left[ \begin{array}{c} \textbf{O}_{7 \times 4} \\ \textbf{I}_{4 \times 4} \end{array}\right] \end{aligned}$$

(5.50)

The procedure is therefore exactly the same as the one highlighted in the previous section. We apply to this augmented formulation Eqs. (5.34)–(5.39), (5.40), (5.41) at each iteration. The only differences reside in the size of states and controls, and in the corresponding non-convex contributions. Moreover, we have different constraints and cost function, described in the next subsections.

B. Constraints

As aforementioned the constraints included in this work, and described by Eqs. (5.20) and (5.21) can be exactly implemented as Second-order conic constraints. For the glide-slope constraint we impose

$$\begin{aligned} \left\| \textbf{A}_{gs}\textbf{r}+\textbf{b}_{gs}\right\| \le \textbf{c}_{gs} \textbf{r}+d_{gs} \end{aligned}$$

(5.51)

with

$$\begin{aligned} \begin{array}{cc} \textbf{A}_{gs} \left[ \begin{array}{ccc} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array}\right] ,&{} \textbf{b}_{gs} = \left[ \begin{array}{c} 0 \\ 0 \end{array}\right] , \vspace{2mm}\\ \textbf{c}_{gs} = \left[ \begin{array}{ccc} 1 &{} 0 &{} 0\\ \end{array}\right] ,&d_{gs} = 0 \end{array} \end{aligned}$$

(5.52)

For the limitations of horizontal position and velocity at the end of the landing phase, we can derive similar expressions:

$$\begin{aligned} \begin{array}{c} \left\| \textbf{A}_{r}\textbf{r}+\textbf{b}_{r}\right\| \le \textbf{c}_{r} \textbf{r}+d_{r}\\ \left\| \textbf{A}_{v}\textbf{v}+\textbf{b}_{v}\right\| \le \textbf{c}_{v} \textbf{v}+d_{v} \end{array} \end{aligned}$$

(5.53)

where the corresponding matrices are defined as

$$\begin{aligned} \begin{array}{cc} \textbf{A}_{r} = \textbf{A}_{v} = \left[ \begin{array}{ccc} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 1 \end{array}\right] ,&{} \textbf{b}_{r} = \textbf{b}_{v} = \left[ \begin{array}{c} 0 \\ 0 \end{array}\right] , \vspace{2mm}\\ \textbf{c}_{r} = \textbf{c}_{v} = \left[ \begin{array}{ccc} 0 &{} 0 &{} 0\\ \end{array}\right] ,&d_{r} = 1,\quad d_v = 0.1 \end{array} \end{aligned}$$

(5.54)

C. Augmented Cost function

The augmented cost is formally the same as Eq. (5.42). However some practical terms will differ due to the application peculiarities since the true cost J, defined respectively by Eqs. (5.15) and (5.24) are clearly distinct. Finally, $w_m$ and $w_u$ are in this case equal to 100 and 10, respectively. To summarize the landing convexified problem we want to minimize at each iteration Eq. (5.42). The solution must satisfy Eqs. (5.34), (5.20), and (5.21) while ensuring proper penalization of both the trust region size through Eqs. (5.37) and (5.39), and of the virtual controls through Eqs. (5.40) and (5.41). Note that since no 6-DoF dynamics is considered in this work no explicit penalization of roll torque commands are included. However, the limitation imposed on the roll rate is such that it will be possible for the attitude control system to track it. In the next section we will transcribe the problem through the use of hp generalized pseudospectral methods.

5.5 Sequential Pseudospectral Convex Programming

The transcription proposed here is conceptually common to both the aerodynamic descent and the powered landing problems. Consequently, we will focus on the aspects common to both first, emphasizing later the differences between the two specific formulations, especially in terms of constraints, cost function, and initialization strategy. The transcription we propose adopts an hp generalized pseudospectral transcription based on the use of flipped Legendre-Gauss-Radau (fLGR) method. This method is a valid alternative to the more traditional Euler and trapezoidal discretization transcriptions, given its higher accuracy. Moreover, its main drawback, i.e., a typically larger CPU time, can be mitigated by proper choice of h and p [20]. In the remainder of this section we will identify the steps of transcription according to the Sequential Pseudospectral Convex Programming (SPCP) method here proposed.

5.5.1 Discretization

Motivated by the good results obtained in our previous works [18, 20] we extend the methodology to the problem formulated in Sect. 5.4. Specifically, we propose to use n segments, and in each of them perform a local collocation using $p+1$ nodes coming from the p roots of the corresponding fLGR polynomial, defined in the domain $\left. \left( {-1,1}\right. \right]$, and initial non-collocated node at $\tau =-1$. A visualization of the domain is visible in Fig. 5.3.

Fig. 5.3

Domain of the hp flipped Legendre-Gauss-Radau method

Note that since the domain is broken into segments, some linking conditions connecting them are needed. They will explicitly be defined in this section, and form, together with the equations of motion and the boundary conditions the set of linear equations underlying the transcription.

Another benefit is associated with the possibility to have an open final-time formulation of the guidance problem. In fact, to come up with a free final-time discretization some researchers prefer to reformulate the problem by using a different independent variable, known to be monotonically changing, and with known initial and final values [31]. A different approach was the use of a stretching term $\hat{\sigma }$ in the equations of motion [27]. This term can be in fact re-interpreted as very close to the typical mapping between physical time and pseudospectral time $k_t$, defined as

$$\begin{aligned} k_t \triangleq \frac{t_F-t_0}{2n} \end{aligned}$$

(5.55)

with $t_0$ and $t_F$ initial and final times of the physical problem to be solved, and n the number of phases to be used in the hp framework we are proposing. This observation helps in rewriting the transcription in presence of free final time as follows. We assume to have the state vector $\textbf{x} \in \mathbb {R}^{n_s}$, the control vector $\textbf{u} \in \mathbb {R}^{n_c}$, the virtual control vector $\mathbf {\nu } \in \mathbb {R}^{n_v}$, and a total of $n(p+1)$ discrete time steps, corresponding to the n segments and the $p+1$ discrete points in each of the segments. Computed the $p+1$ nodes $\tau _i$ corresponding to a single segment and defined between -1 and 1 we can, for every couple $t_0$, and $t_F$, identify the single ith discrete timestep associated with the jth segment as

$$\begin{aligned} t_i^j = t_0+\frac{t_F-t_0}{n}\left( j-\frac{1}{2}\right) + \frac{t_F-t_0}{2n} \tau _i ,j=1,\dots , n-1 \end{aligned}$$

(5.56)

Defined the discrete time domain, we can introduce the augmented discrete decision vector $\textbf{X} \in \mathbb {R}^{n_{var}}$ as

$$\begin{aligned} \textbf{X} = \left[ \begin{array}{ccccccccccccccccccc} \textbf{x}_0^1&\textbf{u}_0^1&\nu _0^1&\cdots&\textbf{x}_p^n&\textbf{u}_p^n&\nu _p^n&\eta _0^1&\cdots&\eta _p^n&\zeta _0^1&\cdots&\zeta _p^n&\mu _0^1 \cdots \mu _p^n&s_\eta&s_\zeta&t_F \end{array} \right] ^T \end{aligned}$$

(5.57)

The first $\left[ n_s+n_c+n_v\right] \left[ n(p+1)\right]$ elements correspond to states, control and virtual controls, respectively. The set of data associated with $\eta _0^1$,$\dots$,$\eta _p^n$ represents the upper bounds on virtual controls, while the variables identified as $\zeta _0^1$,$\ldots$,$\zeta _p^n$ constrain the size of the pointwise trust regions. The variables $\mu _0^1$,$\ldots$,$\mu _p^n$ are associated with the cost function. We can see the presence of the slack variables $s_\eta$ and $s_\zeta$, penalizing virtual controls and trust regions, as they appear in Eq. (5.42). Finally, since the problem has open final time the variable $t_F$ appears as last element of the augmented vector, by assuming, without compromising any possibility of general application of the proposed method, that $t_0 = 0$. This assumption is always applicable by simply shifting the time vector by the initial time of the aerodynamic descent or the powered landing sequence.

5.5.2 Dynamics

Let us consider the dynamics of our system as convexified in Eq. (5.34). By adopting the time mapping of Eq. (5.55) we can rewrite it as follows:

$$\begin{aligned} \dot{\mathbf {{x}}} = k_t\left[ \textbf{A}_c \textbf{x} + \textbf{A}_k\textbf{x} + \textbf{B}\textbf{u} + \textbf{C}\mathbf {\nu }+\textbf{G}_k\right] \end{aligned}$$

(5.58)

where the equation now describes the evolution of the states with respect to a new independent variable $\tau$, defined between –1 and 1, and chosen because it represents the domain of definition of Legendre-Gauss-Radau polynomials [17, 19]. We can use this expression to derive linear system of equations representing Eq. (5.58) in discrete form.

By keeping in mind that only $\textbf{A}_k$ and $\textbf{G}_k$ change at each iteration we can perform an expansion of the right-hand side of Eq. (5.58) with respect to the variables $\textbf{x}$, $\textbf{u}$, $\mathbf {\nu }$, and $t_F$. Let us define the following quantities.

$$\begin{aligned} \begin{array}{l} {\tilde{\textbf{A}}} \triangleq k_t\left[ \textbf{A}_k+\textbf{A}_c \right] \\ {\tilde{\textbf{B}}} \triangleq k_t\textbf{B}\\ {\tilde{\textbf{C}}} \triangleq k_t\textbf{C}\\ {\tilde{\textbf{E}}} \triangleq \frac{1}{2n}\left[ \textbf{f}_{nc}(\textbf{x}_k)+\textbf{A}\textbf{x}_k+\textbf{B}\textbf{u}_k+\textbf{C}\mathbf {\nu }_k\right] \\ {\tilde{\textbf{G}}} \triangleq k_t\textbf{G}_k-\frac{t_{F,k}}{2n}\left[ \textbf{f}_{nc}(\textbf{x}_k)+\textbf{A}\textbf{x}_k+\textbf{B}\textbf{u}_k+\textbf{C}\mathbf {\nu }_k\right] \\ \end{array} \end{aligned}$$

(5.59)

It is straightforward to verify that the equations of motion can be expressed as

$$\begin{aligned} \dot{\mathbf {{x}}} = {\tilde{\textbf{A}}}\textbf{x}+{\tilde{\textbf{B}}}\textbf{u}+{\tilde{\textbf{C}}}\mathbf {\nu }+{\tilde{\textbf{E}}}t_F +{\tilde{\textbf{G}}} \end{aligned}$$

(5.60)

This expression needs to be tailored for the specific domain of choice. In this work we choose to apply the hp-methods as a series of n equally spaced segments, and in each of them we can collocate the differential equations using $p+1$ nodes. This choice is motivated by the fact that we are interested to real-time-capable methods, and therefore we do not focus on refinement methods which iteratively adapt the size and the distribution of the meshes.

The final step is the inclusion of the pseudospectral differential operator. Note that the derivative of the state in the discrete points $\textbf{x}_i$, $i = 1,\ldots ,n$ can be approximated by a matrix $\textbf{D}$ in the form

$$\begin{aligned} \dot{\textbf{x}} \cong \textbf{D}\cdot \textbf{x} \end{aligned}$$

(5.61)

Equation (5.61) tells us that the derivative in one of the discrete points of the domain can be approximated by a linear combination of the values that the variable $\textbf{x}$ assumes over all the discretized points through the coefficients provided by the columns of $\textbf{D}$.

We can exploit this property to finally build the linear matrix representing the equations of motion as follow: defined $\textbf{D}_{i,\dots }$ as the ith row of $\textbf{D}$ we have that for each segment $j \in [1,\ldots ,n]$ and node $i \in [0,\ldots ,p]$

$$\begin{aligned} \textbf{D}_{i,\dots }\cdot \textbf{x}^j_{0,\ldots ,p}-{\tilde{\textbf{A}}}\textbf{x}^j_i-{\tilde{\textbf{B}}} \textbf{u}_i^j -{\tilde{\textbf{C}}} \mathbf {\nu }_i^j - {\tilde{\textbf{E}}}t_F = {\tilde{\textbf{G}}} \end{aligned}$$

(5.62)

which in matrix form can be assembled as

$$\begin{aligned} \textbf{A}_{EoM}\mathbf {{X}} = \textbf{b}_{EoM} \end{aligned}$$

(5.63)

5.5.3 Boundary Conditions

We can augment the previous linear system of Eq. (5.63) by including hard constraints to comply with initial and final states definitions. The corresponding matrix will simply by

$$\begin{aligned} \textbf{A}_{bc}\mathbf {{X}} = \textbf{b}_{bc} \end{aligned}$$

(5.64)

corresponding to

$$\begin{aligned} \textbf{A}_{bc} = \left[ \begin{array}{cccc} I_{n_s} &{} O_{n_s\times (n_t)(n)(p-2)} &{} O_{n_s \times n_s} &{}O_{n_s\times (n_{var}-[(n_t)(n)(p-2)+2(n_s)])} \\ O_{n_s \times n_s} &{} O_{n_s\times (n_t)(n)(p-2)} &{} I_{n_s} &{}O_{n_s\times (n_{var}-[(n_t)(n)(p-2)+2(n_s)])} \\ \end{array}\right] \end{aligned}$$

(5.65)

where $I_{n_x}$ and $O_{n_y \times n_z}$ are the identity matrix and the zero matrix of size $n_x$ and $n_y \times n_z$, respectively, while $n_t = n_s+n_c+n_v$. The vector $\textbf{b}_{bc}$ is intuitively defined as

$$\begin{aligned} \textbf{b}_{bc} = \left[ \begin{array}{c} \textbf{x}(t_0) \\ \textbf{x}(t_F) \end{array}\right] \end{aligned}$$

(5.66)

In case some initial and / or final conditions are left free the corresponding rows in Eqs. (5.65) and (5.66) can simply be deleted.

5.5.4 Linking Conditions

The discretization introduced in Fig. 5.3 requires some extra constraints known as linking conditions or linkage conditions, needed to enforce continuity of the states and controls defined on the edge of the segments. These conditions are represented by equality constraints in the form

$$\begin{aligned} \left[ \begin{array}{c} \textbf{x} \\ \textbf{u} \\ \mathbf {\nu }\end{array}\right] _p^{j} = \left[ \begin{array}{c}\textbf{x} \\ \textbf{u} \\ \mathbf {\nu }\end{array} \right] _0^{j+1} ,\quad j \in [1, n-1] \end{aligned}$$

(5.67)

It is immediate to see that these conditions can be built by assigning identity matrices of consistent dimension to the proper indices of a matrix $\mathbf {A_{lc}}$ with the corresponding vector $\mathbf {b_{lc}} \triangleq O_{n_t \times 1}$.

The overall system of differential equations is therefore given by

$$\begin{aligned} \textbf{A}_{eq}\textbf{X} = \textbf{b}_{eq} \end{aligned}$$

(5.68)

with

$$\begin{aligned} \textbf{A}_{eq} = \left[ \begin{array}{c} \textbf{A}_{EoM} \\ \textbf{A}_{bc}\\ \textbf{A}_{lc} \end{array} \right] ,\quad \textbf{b}_{eq} = \left[ \begin{array}{c} \textbf{b}_{EoM} \\ \textbf{b}_{bc}\\ \textbf{b}_{lc} \end{array} \right] \end{aligned}$$

(5.69)

5.5.5 Cost

For the cost function by recovering Eq. (5.42), and remembering the quadrature expression associated with the hp fLGR method an the continuous expression we can rewrite it as

$$\begin{aligned} J_{aug} = -w_m m_p^n+w_u\frac{t_F-t_0}{2n}\textbf{w}_{fLGR}^T\mathbf {\mu } + w_\nu \cdot s_\nu + w_\zeta \cdot s_\zeta +w_{t_F}s_{t} \end{aligned}$$

(5.70)

where the weights $w_{fLGR}$ are dictated by the fLGR theory [17], and $w_m$ equal to 0 if we refer to the aerodynamic descent, or larger than 0 if referred to the powered landing case. Finally, note that a penalization on the final time variation is included through a corresponding slack variable $s_t$. This variable acts as upper bound on the variation of the final time with respect to the previous one, and is also modeled as conic constraint. Its construction is trivial and skipped to avoid excess of redundancy in the equations.

Remark 3: Note that since we are dealing with open final time problems a formal linearization of the second term in Eq. (5.70), bilinear in the variables $\mu _i^j$ and $t_F$, is needed. For easiness of implementation this linearization is not carried out, and approximated by $\frac{t_{F,k}-t_0}{2n}w_{fLGR}^T\mathbf {\mu }$. This approximation is valid as long as the condition $(t_F-t_{F,k})\textbf{w}_{fLGR}^T\mathbf {\mu }_k \ll (t_F-t_0)\textbf{w}_{fLGR}^T\mathbf {\mu }$ is satisfied. This aspect is omitted here for brevity, but numerically verified during the simulations, and therefore the approximation is valid.

The role of the variables $\mu$ is to act as upper bound for the true elements appearing in the cost function of Eq. (5.15). Given the selected cost function it is immediate to observe that it can be cast in a second-order cone constraint as follows.

$$\begin{aligned} \left\| \begin{array}{c} u_\theta \\ u_\psi \end{array}\right\| _{2,i}^j \le \mu _i^j,\quad \begin{array}{c} i \in [0, p]\\ j \in [1, n] \end{array} \end{aligned}$$

(5.71)

The transcription is completed by applying point-wise the second-order conic constraints representing the upper bound on virtual controls, i.e.,

$$\begin{aligned} \left\| \mathbf \nu _i^j \right\| _2 \le \eta _{\nu ,i}^j,\quad \begin{array}{c} i \in [0, p]\\ j \in [1, n] \end{array} \end{aligned}$$

(5.72)

and on the trust region.

$$\begin{aligned} \left\| {\tilde{\textbf{X}}}-{\tilde{\textbf{X}}}_{k} \right\| _{2,i}^j \le \zeta _i^j \end{aligned}$$

(5.73)

$$\begin{aligned} \left\| \mathbf \zeta \right\| _{2,i}^j \le s_{\zeta ,i}^j,\quad s_\zeta \in \mathbb {R}^{np} \end{aligned}$$

(5.74)

5.5.6 Constraints—Powered Landing

In addition to Eq. (5.71) (opportunely augmented to consider the different number of controls) the constraints of Eqs. (5.20) and (5.21) are also modeled as second-order conic constraints. Therefore, they can simply be applied to each discrete node representing position and velocity.

$$\begin{aligned} \begin{array}{cc} \begin{array}{c} \left\| \textbf{A}_{gs}\textbf{r}_i^j+\textbf{b}_{gs}\right\| _2 \le \textbf{c}_{gs} \textbf{r}_i^j+d_{gs}\vspace{2mm}\\ \left\| \textbf{A}_{r}\textbf{r}_i^j+\textbf{b}_{r}\right\| _2 \le \textbf{c}_{r} \textbf{r}_i^j+d_{r},\vspace{2mm}\\ \left\| \textbf{A}_{v}\textbf{v}_i^j+\textbf{b}_{v}\right\| _2 \le \textbf{c}_{v} \textbf{v}_i^j+d_{v} \end{array} &{} \begin{array}{c} i \in [0,p]\vspace{2mm}\\ j \in [1,n] \end{array} \end{array} \end{aligned}$$

(5.75)

5.5.7 Initialization

For the aerodynamic descent the initial guess for the states is built by using linear interpolation between the desired initial and final states, while the controls were kept equal to 0. For the landing phase a more sophisticated strategy is adopted. A scheme illustrating the SPCP algorithm is depicted in Fig. 5.4. Inspired by the idea of Simplicio et al. [24] we adopt an educated guess, obtained by solving the problem with the method described in [20]. Given the reference scenario the simplified problem is solved with hard constraints for initial and final conditions, as well as for the time of flight, assumed to be fixed. In this initialization solution neither aerodynamic effects, nor control rates are considered, and the gravity is assumed to be constant. Then, the obtained solution is converted into a format compatible with the SPCP transcription illustrated in this section, and utilized as $k^\textrm{th}$ solution, with $k=0$ to start the sequential pseudospectral convex optimization procedure.

The solution obtained contains the thrust vector in Cartesian coordinates, which are converted into the corresponding Euler angle representation by assuming that the x-body axis coincides with the thrust vector. This is a valid assumption since we are dealing with a 3-DOF model. The control rates are then obtained by numerically differentiating the Euler angles and the thrust magnitude profile, completing the information required to build the very first solution according to the format described by Eqs. (5.43) and (5.44). It is then possible to start the sequential pseudospectral convex optimization, and at the end of each iteration the algorithm checks whether convergence has been reached. In negative case the current solution is used to build the new subproblem and iterate the procedure. In the opposite case the procedure is concluded. To validate our solution we perform a feedforward propagation of the full nonlinear equations of motion driven by the computed controls, and compare the obtained solution with the optimized one, which is the outcome of the proposed algorithm.

Remark 4: Note that this further step is not considered to be part of the on-board guidance strategy, but it is only meant as validation tool to measure the effectiveness and the accuracy of the proposed algorithm.

Fig. 5.4

Sequential Pseudospectral Convex Programming (SPCP) scheme

5.5.8 Convergence Criterion

Once the algorithm is initialized the process of generating subsolutions is repeated until convergence is reached. In literature many authors meaningfully use as criterion the difference between subsolutions meant in vector or scalar form [28, 29]. To take into account both the convergence of subsolutions and the cost function we use as stopping criterion the difference between consecutive values of the augmented functions, defined in Eq. (5.70). Although this choice plays no big differences in practical terms, since very close subsolutions will also lead to similar cost functions, it represents a way to account also for the variations of other parts of the algorithms, such as virtual controls and trust region radii, which do not belong to the set of physical variables of the problem. The stopping criterion can be therefore expressed as

$$\begin{aligned} \delta J_{aug} \triangleq \left| J_{aug}^{k}-J_{aug}^{k-1}\right| \le \epsilon \end{aligned}$$

(5.76)

with $\epsilon$ chosen equal to $5\cdot 10^{-5}$ for the aerodynamic phase and to $2 \cdot 10^{-4}$ for the powered landing segment. The choice is dictated by empirical experience showing that given the shorter duration of the powered phase a slightly less stringent criterion is sufficient to reach very good accuracy while limiting the number of iterations, and therefore speeding up the total execution time of the algorithm.

5.6 Numerical Results

This section illustrates results obtained with the proposed method for both types of scenarios. First, we will describe the aerodynamic descent scenario, followed by the powered landing results.

Table 5.1 Aerodynamic descent—initial and final conditions

5.6.1 Aerodynamic Descent—Nominal

For the aerodynamic descent initial and final conditions are described in Table 5.1. Note that all the positions have been scaled with respect to the initial altitude, the scaled gravity is equal to 1, and all the other variables have been scaled consistently with these two assumptions. Results are shown in Figs. 5.5 through 5.11. By looking at the states (Fig. 5.5) we see that the solution shows a smooth behavior while satisfying initial and final conditions. The same holds for the attitude (Fig. 5.6a), where the specific upper and lower bounds for pitch and yaw are met, and the attitude rates, correctly bounded between –10 and 10$^\circ$ (Fig. 5.6b). The overall trajectory is depicted in Fig. 5.7, where the body axes (in RGB convention) depict the corresponding attitude while performing the aerodynamic descent. The associated aerodynamic behavior is visible in Fig. 5.8a, showing the normalized aerodynamic forces in body axes. Note that to further enhance the 6-DOF feasibility of the solution the aerodynamic forces are computed by dynamically trimming the vehicle. To verify the correct behavior of the solution the resulting aerodynamic torques with respect to the center of mass are stored and observed. The normalized aerodynamic torque residuals are depicted in Fig. 5.8b, and are close to the zero-machine. The trimming is realized by opportunely deflecting the four fins, which ensure that the aero-torque disturbances are nullified while satisfying the maximum allowed fin deflections (shown in normalized coordinates in Fig. 5.8c).

Fig. 5.5

Aerodynamic guidance solution—translational states

Fig. 5.6

Aerodynamic guidance solution: a Attitude states, and b Attitude rates

Fig. 5.7

Aerodynamic guidance solution—trajectory: the body axes are depicted in red (X), green (Y), and blue (Z)

Fig. 5.8

Aerodynamic guidance solution: a Aerodynamic forces, b Aerodynamic torques, c Fin deflections

Fig. 5.9

Nominal solution validation: a comparison of states, and b difference between optimized and propagated states

Fig. 5.10

Convergence behavior: a Cost function, b Augmented cost function, c virtual control upper bound, d trust region upper bound, e final time variations, and f acceptance/rejection decision

For what regards the accuracy of the solution a full propagation of the trajectory by using the full set of nonlinear equations is performed, and depicted in Fig. 5.9a, with the mismatch between the two profiles visible in Fig. 5.9b. The two solutions agree very well, with a maximum scaled error in the order of $4\cdot 10^{-4}$ for the position and $2\cdot 10^{-3}$ for the velocity. In full scale these results correspond to meter-error for the position, and less than 0.5 m/s for the velocity. The convergence behavior is depicted in Figs. 5.10a through 5.10f. The first thing to observe is the behavior of the cost and the augmented cost, shown in Fig. 5.10a and b. At the beginning of the process larger variations between solutions are experienced. From iteration 4 to the end the algorithm converges to a specific solution, and therefore the upper bounds on trust regions and virtual control fade away. As a consequence the two profiles converge to very similar values. The reduction of virtual controls and trust regions can be seen in Fig. 5.10c and d. We can see that starting from the second iteration the method does not really rely on virtual controls, meaning that the actual controls are sufficient to solve the convex subproblems. The trust regions upper bound becomes smaller than $10^{-3}$ starting from the $7^\textrm{th}$ iteration, and no sensitive variations of the augmented cost function and of the solution are observed. Finally, we can observe that the final time variations between consecutive solutions rapidly decreases too (Fig. 5.10e). Note that as further test the initialized final time is given as the converged final time + 10 s to observe whether the algorithm was able to come back to the optimal value. This behavior is confirmed by looking at the first iteration, where a variation of about 9 s is observed, followed by smaller variations along the successive iterations. The last plot on the bottom right (Fig. 5.10f) shows the decisions of keeping or rejecting the subsolution along the iterations. A subsolution is rejected in two cases: first, when the SOCP solver returns an infeasibility status, or if the maximum number of iterations is reached without finding a valid solution, with the iteration limit for the SOCP solver set equal to 100. This issue did not occur in the results shown here, as confirmed by Fig. 5.10f.

To give an intuitive idea of the convergence process we plot the several subsolutions obtained over the iterations in Fig. 5.11, showing the translational states. The process is initialized with a trivial linear interpolation between initial and final desired states (in blue). After three iterations the solution is already resembling the final one (in red), that is only refined in the remaining iterations. This is a consequence of having variable trust region upper boundaries, which allow larger variations at the beginning if needed, and are dynamically reduced, making, iteration after iteration, the linearized dynamics more and more able to capture the behavior of the nonlinear differential equations underlying the problem.

Fig. 5.11

Convergence behavior: evolution of translational states

5.6.2 Aerodynamic Descent—Dispersed Cases

As further test we simulated 25 dispersed cases associated with different initial conditions in terms of position and velocity for both the aerodynamic and the powered landing phases. Note that these cases are purely demonstrative and of course not representative of a full Monte-Carlo campaign. However, they confirm the capability of the algorithm to generate valid solutions over a much larger set of conditions than the one given by the nominal scenario. Specifically, since it is assumed that the aerodynamic guidance algorithm is triggered at a specific altitude, errors in terms of crossrange and downrange components have been considered for what regards the position. These errors are equal to 200 m, whereas all the three components of the velocity are perturbed up to $\pm 15$ m/s. All the perturbations are uniformly distributed. Figures 5.12 and 5.13 show the resulting trajectories, together with the translational and the rotational states. Moreover, the Runge-Kutta validation of the obtained solutions are depicted in Fig. 5.14a and b. All the trajectories converged to the prescribed interface conditions while satisfying the constraints. Moreover, from the validation of the solutions (Fig. 5.14a–b) we can see that all of them fully satisfy the equations of motion, with a consistently small error between propagated and optimized states.

Fig. 5.12

Aerodynamic guidance solution—dispersed trajectories

Fig. 5.13

Aerodynamic guidance solution: a Attitude states, and b Attitude rates

Fig. 5.14

Dispersed solutions validation: a Comparison of states, and b Difference between optimized and propagated states

5.6.3 Powered Landing—Nominal

The prescribed initial and final conditions for the powered landing scenario we are dealing with are described in Table 5.2. The weights $w_{vc}$ and $w_{tr}$ are equal to 500 and 10. We keep the same penalization of final-time variations as for the aerodynamic descent. States, and controls are depicted in Figs. 5.15 and 5.16. Besides a smooth solution also in this case with initial and final boundaries fully satisfied we can see that in the last phase of landing the horizontal components of position and velocity are correctly constrained too, and so is the glideslope constraint (here omitted for brevity). Moreover, the attitude rates always lie in the prescribed boundaries, and the vehicle shows a vertical attitude when landing.

Table 5.2 Powered landing—initial and final conditions

Fig. 5.15

Landing guidance solution—translational states

Fig. 5.16

Landing guidance solution: a Attitude states, and b Attitude rates

Fig. 5.17

Landing guidance solution: throttle, throttle rate, and normalized mass

Fig. 5.18

Landing guidance solution—trajectory x-body is in red, y-body in green, z-body in blue

Fig. 5.19

Landing guidance solution: a Aerodynamic forces, b Aerodynamic torques, c Fin deflections

Fig. 5.20

Nominal solution validation: a Comparison of states, and b Difference between optimized and propagated states

Fig. 5.21

Convergence behavior: a Cost function, b Augmented cost function, c Virtual control upper bound, d Trust region upper bound, e $t_F$ variations, and f Acceptance/rejection policy

Fig. 5.22

Convergence behavior—translational states

The throttle profile, with its corresponding throttle rate and mass profiles are shown in Fig. 5.17. All of them are within the prescribed limits. The attitude is visible also in Fig. 5.18, while the corresponding aerodynamic forces and torques are depicted in Fig. 5.19a and b. Note that the forces are computed also in this case by taking the attitude controllability into account, such that the aerodynamic torque is constantly minimized (Fig. 5.19c). Specifically, only 15% of the fin maximum deflections is sufficient to remove the undesired aerodynamic torque that would from having fin deflections equal to $0^{\circ }$. Since the effectiveness of fins decreases with the dynamic pressure, at the pseudotime equal to approximately 0.65 the fins are disabled and the TVC can continue to control the attitude until touchdown occurs. Finally, as depicted at the end of the scheme of Fig. 5.4, a validation through Runge-Kutta 45 is performed to verify that the obtained solution satisfies the full nonlinear equations of motion. The results are visible in Fig. 5.20a and b. Note that the solution perfectly matches the propagated one, with an error that in full scale is in the order of 0.02 m for the position components, and below 0.1 m/s for the velocity components. We can have a look at the convergence properties of the algorithm: (Fig. 5.21a–f). First, by looking at Fig. 5.21a we can see that no big changes are observed in the original cost function. This means that the mass consumption remains approximately the same, whereas the algorithm focuses on the refinement of the trajectory. This is confirmed by the augmented cost in Fig. 5.21b, where we can see that after iteration 2 no big variations occur anymore. The upper bounds on virtual controls (Fig. 5.21c) is constantly equal to $10^{-10}$, meaning that the algorithm is always able to obtain a solution without actively leveraging the use of virtual controls for this specific scenario. Good convergence properties are visible also from the variation of the upper bounds on trust regions (Fig. 5.21d), which at the end of the iterative process is in the order of $2\cdot 10^{-4}$. The same behavior is visible for the variations of $t_F$, shown in Fig. 5.21e. After iteration 2 the variations on the final time are always smaller than 0.1 s, and become negligible after iteration 4.

The convergence process in terms of acceptance/rejection is depicted in Fig. 5.21f. All the solutions are accepted, confirming that the proposed approach shows good feasibility. Finally, the convergence behavior can be also seen in Fig. 5.22, where the colormap moves from blue to red as the number of iterations goes from the first to the last iteration. All the states quickly converge to the final solution. This figure shows that the initialization strategy correctly captures most of the behavior, simplifying the work of the SPCP algorithm. Note however, that whenever this is not the case, the SPCP was nevertheless able to correct the violations, as previously shown in [21].

5.6.4 Powered Landing—Dispersed Cases

Also in this case we did a preliminary analysis of the algorithm in presence of dispersions on the initial conditions in terms of position and velocity, as well as for the attitude. The errors on crossrange and downrange position are uniformly dispersed up to ± 50 m, while for the three velocity components the error is up to ±5 m/s. Moreover, up to 2.5$^\circ$ error is added to the initial pitch and yaw angles. Figures  5.23 and 5.24 show the resulting trajectories, together with the translational and the rotational states. Moreover, the Runge-Kutta validation of the obtained solutions are depicted in Fig. 5.25a and b.

Fig. 5.23

Powered landing guidance solution—dispersed trajectories

Fig. 5.24

Powered landing guidance solution: a Attitude states, and b Attitude rates

Fig. 5.25

Dispersed solutions validation: a Comparison of states, and b Difference between optimized and propagated states

Also in this case all the trajectories fullfill the requirements (Fig. 5.23) and all the states and control limitations are satisfied (Fig. 5.24). Finally also in this case from the point of view of the accuracy of the solution we obtain a consistent ensemble of trajectories that accurately capture the nonlinear behavior of the system (Fig. 5.25a), and show a maximum error of approximately $7\cdot 10^{-4}$ in position, and $4\cdot 10^{-4}$ in velocity.

5.7 Conclusions

In this chapter we proposed an approach able to deal with both the aerodynamic descent and the powered landing phases of a reusable rocket. In the former case the control means are represented by the attitude of the vehicle with respect to the airspeed, which induces the aerodynamic forces that effectively drive the motion of the rocket during the unpowered descent, while in the latter these contributions are effects to be coupled with the thrust force, which is the main control means during the landing phase.

The approach exploited the distinction between convex and non-convex terms to come up with a convex sub-problem in which the need of numerical linearization is reduced to the sole non-convex terms. The reformulation of the problem in terms of rates of Euler angles allowed to express the system in affine form, with the corresponding benefits in terms of convergence behavior. Moreover, a transcription based on hp pseudospectral methods allowed on one side to improve the accuracy of the obtained solution, and on the other side to naturally formulate the free-final time version of the problem.

Numerical results for nominal and dispersed condition confirm that the proposed approach is a viable method to quickly solve both the aerodynamic and landing guidance problems while providing at the same time a very accurate solution, with errors in the meter-range for what regards position, and less than 0.2 m/s in terms of velocity. The method is therefore a candidate technology to cover the entire descent guidance problem associated with the use of reusable rockets.