Autonomous Guidance Control for Ascent Flight

Abstract

The purpose of the guidance control is to release a payload into a prescribed target orbit (PTO) accurately. The parameters that determine an orbit are called orbital elements (OEs), which include the semi-major axis a, the eccentricity e, the argument of perigee $\omega$, the inclination angle i, and the longitude of ascending node (LAN) or the right ascension of ascending node (RAAN) $\Omega$, where a and e can be converted to the perigee height $h_p$ and the apogee height $h_a$. Thus, the guidance mission of a launcher is a typical optimal control problem with multi-terminal constraints, which requires complex iterative calculations. Considering various constraints in practical applications, such as the accuracy of inertial navigation systems and the performances of embedded computing devices (speed and storage capacity), guidance methods need to balance the mission requirements, hardware resources, and algorithm complexity. A variety of guidance methods has been developed with distinct era characteristics.

2.1 Introduction

The purpose of the guidance control is to release a payload into a prescribed target orbit (PTO) accurately. The parameters that determine an orbit are called orbital elements (OEs), which include the semi-major axis a, the eccentricity e, the argument of perigee angle $\omega$, the inclination angle i, and the longitude of ascending node (LAN) or the right ascension of ascending node (RAAN) $\Omega$, where a and e can be converted to the perigee height $h_{\!p}$ and the apogee height $h_{a}$. Thus, the guidance mission of a launcher is a typical optimal control problem with multi-terminal constraints, which requires complex iterative calculations. Considering various constraints in practical applications, such as the accuracy of inertial navigation systems and the performances of embedded computing devices (speed and storage capacity), guidance methods need to balance the mission requirements, hardware resources, and algorithm complexity. A variety of guidance methods has been developed with distinct era characteristics.

2.1.1 Traditional Guidance Methods

(1) Guidance methods in early stage

The early guidance methods of the ascent phase for launchers in various countries were open-loop guidance (OLG) methods [1,2,3]. In these solutions, an off-line trajectory to the PTO was planned in advance, including the time-varying position, velocity, and thrust directions (guidance commands). After liftoff, the guidance commands in the corresponding flight phases were interpolated based on the trajectory by taking the time, velocity, or altitude as the independent variable. In general, the command interpolated over time consumes more fuel than that over the velocity. OLGs usually transform the OEs into terminal velocity and position constraints at the prescribed injection point, and they perform well to meet the load limit requirements when flying in the atmosphere using a wind biasing trajectory based on the wind field of the launch day [4].

The perturbation guidance method (PGM) was developed to further improve the injection accuracy, and its guide coefficients were designed offline based on the flight profiles and the most concerned OEs. The state variables of the velocity and position were fed back into the guidance loop, then their deviations to the nominal values were calculated, and the guidance commands were initiated therefrom to guide the launcher to fly as close to the nominal trajectory as possible [5,6,7,8]. PGMs have been applied to launchers since the 1950s, when the guide control could only be conducted first on a simple computing device (which cannot be regarded as a computer). The algorithm was very simple during the early stage, and all the complex operations, such as the calculation of the gravity of Earth, could not be completed onboard. For example, the PGM of the Long March launch vehicles (LMLVs) proposed by Cui et al. generated the guide commands onboard based on interpolation tables [7]. Combined with the perturbation cutoff equations, a better separation control accuracy was obtained [8,9,10]. Considering that the precision of the inertial devices was also low at that time, the PGM had been applied for a long time.

With the development of avionics, the computational bottlenecks on the guidance methods have been greatly eliminated, and PGMs have also further developed. For instance, the simplified apparent velocity accumulation has evolved into explicit navigation calculations. The influence of the second-order term of gravity has also been involved in the algorithms, and more OEs, not just those most concerned ones, can be satisfied by segmented or weighted guide controls.

Compared with OLGs, PGMs calculate guide commands online, exhibiting a certain degree of autonomy. However, if the control deviations increase, the hypotheses of the first-order linearization in the design of guide coefficients cannot hold, which greatly degrades the performance of the PGMs.

(2) Explicit guidance methods

Explicit guidance methods calculate guidance commands in real-time based on the explicit expressions of control functions, which are generally applied when the rocket enters into the vacuum environment. Owing to the release of the wind loads on the vehicle’s structure in a vacuum, an optimal guidance command can be derived by closed-loop guidance (CLG) algorithms. The OEs of the PTO can be directly taken as the terminal constraints, which greatly improves the adaptability and injection accuracy [11]. Typical analytical CLG methods include the iterative guidance mode (IGM) [11,12,13,14,15,16] for rockets, the powered explicit guidance (PEG) [17,18,19] for the space shuttles, and the optimal guidance (OPGUID) [20, 21] based on variational methods.

The IGM could iteratively calculate the required velocity and position increments to the PTO, and then plan the optimal flight path [13, 14]. The earlier the IGM is called, the more complex the algorithm is, because the flight profile covers more flight phases, but the stronger the fault adaptability becomes. The development in IGM boosted the progress of the rendezvous and docking (RVD) missions in China’s manned spaceflight project, where the IGM across two continuous powered phases was first used in the LM-2F/Y8 mission in November 2011. After this, a prediction-correction IGM was adopted for LM-7, which achieved high injection accuracies under high thrust conditions without terminal velocity correction systems. In September 2020, the IGM with a terminal attitude constraint was first utilized in the LM-2F/T3 mission, and the OEs and terminal attitudes were well controlled simultaneously without a reaction control system (RCS) [15]. The IGM across the coasting phase was first used in the maiden flight of LM-8 in December 2020.

The abort or termination requirements during ascent were required for the space shuttles, allowing them to return safely or enter into a pre-set parking orbit if one main engine failed. Thus, a semi-analytical prediction-correction algorithm, i.e., PEG, was proposed. It was a kind of linear tangent guidance, assuming that the thrust direction vector satisfies the linear tangent control laws from the point of view of fuel minimization, and then the guidance law was derived based on the variational method. The covariates were solved based on the required velocity increments, corrected by estimating the velocity deviations at the shutdown time [19]. The number of OEs that must be satisfied can be selected to meet the different mission needs, and the scenario of returning after failures is also considered by the PEG.

OPGUID had been regarded as a backup for the IGM and PEG from the era of the Saturn rockets to the space shuttles. It could meet all the necessary optimality conditions, including the Euler-Lagrange equations, but its maturity is still considered to need improvement.

IGM and PEG exhibit basically the same performances in terms of adaptability, robustness, target performance, and flexibility when confronted with engine faults, while the advantages of the OPGUID lie in its fewer assumptions [21]. In addition, an early release IGM (ERIGM) was studied to be applied before entering the vacuum [1]. The restrictions of the rocket structure caused by the aerodynamic loads when passing through high-dynamic-pressure or high-wind regimes are taken as the constraint of the output commands. Although the assumption of ERIGM’s analytical expression in a vacuum is not satisfied in the atmosphere, the simulation analysis shows that compared with the combination of OLG + IGM, the ERIGM can improve the launch performance while maintaining a smaller dispersion of the terminal states.

2.1.2 Autonomous Guidance Methods

Autonomous guidance methods (AGMs) in and out of the atmosphere have become a popular research topic since 2016, aiming to improve flight autonomy under various scenarios. AGM is a kind of method to dynamically generate the current guidance command based on real-time trajectory planning, while satisfying the process and terminal constraints of all the following flight phases. It does not rely on but also does not exclude the reference trajectory planned off-line, and it can deal with complex, time-varying, and nonlinear constraints onboard, exhibiting strong adaptability and robustness.

2.1.2.1 Related Studies

The analytical CLGs based on the optimal control theory under vacuum conditions, i.e., IGM, PEG, and OPGUID, can also be regarded as the first generation of AGMs. With the upgrading of the onboard computing power, the online trajectory planning methods, which mainly include indirect [22,23,24] and direct methods [25,26,27], were developed and backed by numerical calculations. If their planning period meets the real-time requirements, they may replace the existing analytical methods; if not, a combination of “on-line planning + tracking guidance” can be adopted. Currently, many new concepts related to guidance control have been proposed, reflecting some aspects of the features of AGMs:

(1) Computational guidance

In 2016, the Journal of Guidance, Control, and Dynamics published a special issue of Computational Guidance and Control [28] and pointed out that the control laws and controllers with fixed structures in traditional guidance and control will be replaced by algorithms, which are different from other branches of computational engineering and science. The commands of computational guidance would be model- or data-based, and there is no need for in-advance planning, gain adjustment, or a large amount of off-line design for the nominal state. Thus, computational guidance can be regarded as a special and possibly the main solution strategy for AGMs.

(2) Model-based real-time optimization

At the 2016 Aerospace Conference, it was suggested that model-based real-time optimization is the main direction of future research. It can deal with complex constraints [29, 30], and overcome the shortcomings of traditional real-time optimal control methods which only handle unconstrained or simply constrained problems Therefore, model-based optimization can be regarded as the main research area of AGMs.

(3) Autonomous mission planning

This concept was first found in NASA’s project “Flight Autonomy”, which can be regarded as a higher-level representation of AGMs. If the mission planning can be conducted in real-time, its effect is equivalent to that of AGMs. Four elements of autonomous mission planning [31], such as automatic operators, intelligent initial guesses, powerful optimization software, and technologies supporting online real-time operations, are also the key factors of AGMs.

(4) Adaptive guidance

The adaptive guidance and mission planning were proposed in the roadmap of aerospace intelligent systems drafted by the AIAA Intelligent Systems Technical Committee [32]. These technologies would learn and optimize the system behavior, optimize the aerodynamics and performances of propulsion systems, and solve challenging problems such as the real-time aerodynamic control optimization, convergence of onboard optimization, computational efficiency, adaptive control with sensor constraints, and the security cost of over-optimization. Adaptive guidance reveals the main features and requirements of AGMs.

(5) Adaptive optimal guidance

It was reported by Russian scholars at the 2016 International Astronautical Congress [33] that the three lost global navigation satellite system (GLONASS) satellites launched on December 5, 2010 might have been saved if adaptive optimal guidance had been applied. This method adopts model-based numerical optimization, making full use of the upper stage’s carrying capacity to compensate for the performance degradation of the former stages and re-planning the flight path to the PTO. This solution was similar to the “End to End” (E2E) space mission planning architecture [34], which refers to a multi-stage simultaneous optimization from launching to the final destination. From this point of view, adaptive optimal guidance or E2E planning emphasizes the global optimization feature of AGMs.

All the above-mentioned technologies aim to deploy the payloads to the PTO, even facing unexpected conditions. The potential assumption is that the PTO is reachable, which is reasonable under normal conditions or with enough margin of performance left when a failure occurs.

(6) Fault-tolerant guidance (FTG)

If the PTO is unreachable under failure conditions, the propellant will be exhausted during the flight to it, and the terminal velocity and position may not ensure a parking orbit, causing the rocket/satellite to crash into the ground. The FTG is proposed to reconstruct the mission under this situation [35] to avoid a complete loss, because the well studied fault-tolerant control cannot overcome the effect of gravity to enter into an orbit. Thus, FTG represents an important application scenario of AGMs.

The failures of thrust drop do occur in space launches, but if the PTO is still reachable, either IGM or PEG is capable of re-planning the flight path and releasing the payloads to it. For the Space Launch System (SLS) of NASA, the mission abort design was studied when the target was no longer reachable, but the strategy was based on the off-line simulation and loaded into the onboard computer in advance. It was reported that the Artemis I 1 flight software would pre-upload nine alternative targets. However, only autonomous rescue measures can fully use the remaining carrying capabilities of the launcher to save a mission or avoid crashing down to the ground.

2.1.2.2 Features of AGMs

AGMs are significantly different from OLGs and have a wider range than the traditional CLGs, and could satisfy the demands of research institutions and experts to improve flight autonomy.

AGMs are not synonymous with the trajectory optimization. Trajectory optimization is usually planned off-line, and the result is used as the reference for the tracking control of the launcher. However, the trajectory is generally designed according to the nominal state and cannot predict all disturbances and uncertainties inflight, then the actual flight path usually deviates from the prescribed trajectory. Moreover, trajectory optimization is time consuming, but this is tolerable and the real-time feature is not a key factor for off-line planning. Numerical computing is applied in the trajectory optimization which can consider as many constraints and variables as possible. Even if the planning is not convergent, it can be stopped by human interventions or reset by a new initial guess.

In recent years, trajectory optimization has gradually been adopted for onboard applications, such as the online trajectory optimization, where the constraints and variables it deals with are tailored to facilitate onboard processings, and the dynamic trajectory planning, representing the on-line, real-time, and iterative planning. The former plans the trajectory once or several times followed by the tracking control. The latter is mostly equivalent to AGMs if the frequency of the dynamic planning is almost the same as that of the guidance control. However, only a PTO and no mission reconstruction is considered by these trajectory optimization technologies.

AGMs have the following four distinct features:

• (1) Online. This sets a high demand for the real-time performance of the algorithms and onboard computers. Although a prescribed flight path is no longer required, it can be used as the initial guess to accelerate the online computing.

• (2) Dynamic. Planning is scheduled in each guidance cycle, sometimes called the iterative optimization. The shorter the period of planning is, the stronger the adaptability to uncertainties and interferences becomes. Only the current command of the newly planned results is used for the real control. This process is repeated in the next guidance cycle.

• (3) Global. Each planning process obtains a whole flight path from the initial states, e.g., the current velocity, position, and mass, to the terminal constraints. This is quite different from rolling optimizations, where only a short time period of dynamics is involved.

• (4) Reconstructing. When the PTO is impossible to be reached (often caused by propulsion system faults), it can reconstruct the flight profile or mission target to match the remaining carrying capacity, so as to save the mission or avoid irretrievable disasters as far as possible.

The challenges faced by rockets for the autonomous guidance are also different from those faced by automobiles and civil aircrafts.By taking into account the practices of automobile industries, mission planning and guidance methods are no longer strictly distinguished.

• (1) For automobiles, the planning problem is rules or process based. They basically drive in planar motions under relatively certain environments and operations on road networks with determined risk levels. When an emergency issue occurs, there is not more than one minute to switch from a cruising state to a safe state, such as resting on the roadside and waiting for conditions to improve. They have many control modes, such as forward motion, backward motion, steering, acceleration, deceleration, pausing, and restarting. The difficulties lie in the time-varying dynamic interactions with other vehicles, pedestrians, traffic conditions, and road markings, as well as driving rules.

• (2) Civil aircrafts usually fly in prescribed routes at fixed altitudes except for takeoff and landing. They also have high control abilities, such as the forward motion, upward motion, downward motion, steering, acceleration, and deceleration. The main challenges lie in handling uncertainties autonomously, including the local climate phenomena, variable weather, sudden surges, and out-of-service airports due to delays. They are sensitive to climate conditions, such as the airflow, gales, and thunderstorms. Emergency treatment is definitely needed considering the available fuel, alternative airports and their altitudes, runway lengths, and slope constraints, extended flights in harsh terrain (such as mountains or wilderness), and possible survival concerns.

• (3) Launchers are usually insensitive to abrupt climate changes, because they fly across the atmosphere very quickly, and there are no dynamic constraints similar to that of civil vehicles. The planning problem is strongly nonlinear due to the gravitational and OE constraints. In fault conditions, there is no prescribed parking orbit similar to alternative airports or roadsides, and finding an optimal rescue orbit onboard is very challenging. The control modes are limited, and no descent or stop inflight is available. The amplitude of the thrust is usually fixed, and only the thrust direction can be adjusted. Unlike automobiles or aircrafts, there are no database supports or high-performance computing platforms onboard, even if a database is available.

The problems concerning various vehicles are different in terms of the guidance control or mission planning. Except for the abrupt changes of the climate and dynamic constraints, the AGMs of a launcher face more challenges. This is partly due to the stronger nonlinearity in the optimization problem mainly induced by the gravitational force, the terminal constraints, and a wider range of mass changes, while the other reasons mainly lie in the weaker computing power of the on-board computer (OBC) compared with those on automobiles or aircrafts.

AGMs can relax the pressure of attitude control. If the control deviations exist in each guidance cycle, the accumulated errors can be eliminated in line with a newly planned trajectory in the next cycle, and the influence of errors is retained within a very short planning period. Thus, AGMs improve the robustness of a launcher to disturbances or uncertainties.

It would become difficult to obtain analytical solutions with the increased number of variables that need to be determined, however, an analytical solution after simplifying the problem is a preferable initial guess for AGMs. Even so, AGMs cannot solve too many constraints without affecting the computational efficiency, and hundreds of milliseconds of the solving time are the maximum tolerance. Further, divergence should be avoided in AGMs, but if it does occur, some countermeasures must be scheduled in advance.

2.1.3 Summary

The history of ascent guidance methods applied in LMLVs is introduced here to sum up the above discussion. The three stages are explained in Fig. 2.1, reflecting the changes of the mission requirements and the evolution of the guidance methods. The latter two stages in Fig. 2.1 represent two typical applications of AGMs:

Fig. 2.1

Evolution of ascent guidance methods for Long March rockets

(1) Closed-loop guidance methods for determined target orbit

When the target orbit is determined (i.e., the target matches the carrying capacity), traditional or enhanced analytical methods can play a very good role in the extra-atmospheric flight. For example, although the IGM shows weakness in large arc flight profiles owing to its simplified mean gravitational field assumption, this can be solved by the segmented processing if a coasting phase is inserted. An enhanced PEG algorithm is also being developed by the SLS to adapt to extended flight times.

When flying in the atmosphere, the landing restrictions of the launcher’s jettisons, such as the separated boosters and fairing, should be seriously considered. Then, tracking control is still a relatively safe method under this condition to ensure that the debris falls within a predictable area. Sun and Lu proposed the homotopy method to deal with the atmospheric density onboard for the ascent guidance control, and it showed a certain adaptability to the main engine thrust loss [22]. However, the constraints of the landing area were not considered.

(2) Simultaneous optimization of target orbit and flight path

This only occurs when the PTO is no longer reachable and a new target orbit should be determined. Onboard joint optimization of the new orbit and flight path is very difficult, so a special failure mode, called “engine out,” is considered in the SLS, and a similar approach was also used by the space shuttle. NASA expects a successful mission even if one engine cuts off prematurely, so a sufficient performance margin is definitely needed. When facing severe failures, the SLS can make decisions based on the pre-uploaded alternatives, as introduced in sections above. In recent years, the studies of the autonomous dynamic trajectory optimization under typical failure modes have been initiated for LMLVs and obtained positive results.

At present, few studies on ascent AGMs have been publicly published when considering the needs of mission re-constructions.

2.2 Motion Models of Launchers

2.2.1 Motion Models

The differential translational motion is usually described in the launch inertial coordinate system (LICS) and is shown as follows:

$$\begin{aligned} \begin{array}{l} \boldsymbol{\dot{r}} = \boldsymbol{V},\\ \boldsymbol{\dot{V}} = \frac{{{\boldsymbol{F}_T} + {\boldsymbol{F}_R} + {\boldsymbol{F}_A} + {\boldsymbol{F}_s} + {\boldsymbol{F}_e} + {\boldsymbol{F}_D} + \boldsymbol{G}}}{m},\\ \dot{m} = - \frac{{\left( {\left\| {{\boldsymbol{F}_T}} \right\| - {S_e}\left( {{P_e} - {P_a}} \right) } \right) }}{{{I_{sp}}{g_0}}}, \end{array} \end{aligned}$$

(2.1)

where $\boldsymbol{r}$ is the position vector, $\boldsymbol{V}$ is the velocity, $\boldsymbol{G}$ is the gravity. $\boldsymbol{F}$ is the other forces acting on the vehicle, and the subscripts T, R, A, s, e, and D represent the engine control, RCS, aerodynamic, sloshing, elastic, and interference torques, respectively. $I_{sp}$ is the specific impulse of the engine, $S_e$ is the cross-sectional area of the nozzle, $P_e$ is the atmospheric pressure in the design state, $P_a$ is the external atmospheric pressure inflight, m is the mass, and $g_0$ is the gravitational acceleration of the sea level. The origin of the LICS is the launch point, the x-axis points in the launch direction in the horizontal plane of the launch site, and the y-axis points to the sky along the connecting line between the earth center and the launch point. The z-axis satisfies the right-hand rule.

The aerodynamic force is related to the shape of the launcher and the dynamic pressure inflight, which can be expressed as

$$\begin{aligned} {\boldsymbol{F}_A} = q{S_A}{\boldsymbol{C}_A}. \end{aligned}$$

(2.2)

where q is the dynamic pressure, $S_A$ is the reference area, ${\boldsymbol{C}_A}$ is the aerodynamic coefficient related to the altitude, Mach number, angle of attack, and sideslip angle.

The differential rotational motion is usually described in the vehicle’s body coordinate system (BCS). The origin of the BCS is located at the center of mass of the launcher, the $x_1$-axis points to the head along the body axis, the $y_1$-axis is perpendicular to the longitudinal symmetry plane of the launcher and points upward, and the $z_1$-axis satisfies the right-hand rule.

The following equations reflect the influence of torques on the angular velocity of the launcher:

$$\begin{aligned} \boldsymbol{\dot{\omega }J} = {\boldsymbol{M}_T} + {\boldsymbol{M}_R} + {\boldsymbol{M}_A} + {\boldsymbol{M}_s} + {\boldsymbol{M}_e} + {\boldsymbol{M}_D} - \boldsymbol{\omega } \times \boldsymbol{J\omega }. \end{aligned}$$

(2.3)

where $\boldsymbol{\omega }$ is the angular velocity rotating around the axial direction, $\boldsymbol{J}$ is the moment of inertia, and $\boldsymbol{M}$ is the torque acting on the rocket.

$$\begin{aligned} {\boldsymbol{M}_A} = \left( {{{q{S_A}{l_A}\boldsymbol{C}_d^\omega \boldsymbol{\omega }} / {\left\| \boldsymbol{V} \right\| }} + q{S_A}{l_A}{\boldsymbol{C}_d}} \right) , \end{aligned}$$

(2.4)

where $l_A$ is the reference length, $\boldsymbol{C}_d$ is the aerodynamic torque, and $\boldsymbol{C}_d^\omega$ is the damping coefficient.

$$\begin{aligned} {\boldsymbol{M}_e}\mathrm{{ = }}\sum \limits _i^{} {(b_{1i}^\varphi {{\dot{q}}_i} + b_{2i}^\varphi {q_i})} , \end{aligned}$$

(2.5)

where $q_i$ is the i-th order elastic generalized coordinate, $b_{1i}^\varphi$ and $b_{2i}^\varphi$ are the i-th order elastic additional moment coefficients.

The propellant sloshing moment can be divided into three parts: normal, transverse, and axial. For example, the propellant normal sloshing moment (${M_{s3}}$) is

$$\begin{aligned} {M_{s3}} = \sum \limits _p^{} {(b_{4p}^{{\omega _3}}\Delta {{\ddot{y}}_p} - b_{5p}^{{\omega _3}}\Delta {y_p})} , \end{aligned}$$

(2.6)

where $\Delta y_p$ is the p-th order longitudinal sloshing displacement, $b_{4p}^{{\omega _3}}$ and $b_{5p}^{{\omega _3}}$ are the interaction coefficients of the sloshing moment and sloshing centroid in the pitch channel.

The modeling of the elastic vibration is established according to the finite element method [36]:

$$\begin{aligned} \begin{array}{l} {{\ddot{q}}_i} + 2{\zeta _i}{\varpi _i}{{\dot{q}}_i} + \varpi _i^2{q_i} = \\ D_{1i}^{{\omega _{\mathrm{{z1}}}}}{\omega _{z1}} + D_{2i}^{{\omega _{\mathrm{{z1}}}}}{\alpha _3} + D_{3i}^{{\omega _{\mathrm{{z1}}}}}{\delta _{{\omega _{\mathrm{{z1}}}}}} + D_{3i}^{''{\omega _{\mathrm{{z1}}}}}{{\ddot{\delta }}_{{\omega _{\mathrm{{z1}}}}}}\\ + \sum \limits _p^{} {(G_{ip}^{''{\omega _{\mathrm{{z1}}}}}\Delta {{\ddot{y}}_p} + G_{ip}^{{\omega _{\mathrm{{z1}}}}}\Delta {y_p})} + \sum \limits _j^{} {(R_{ij}^{'{\omega _{\mathrm{{z1}}}}}{{\dot{q}}_j} + R_{ij}^{{\omega _{\mathrm{{z1}}}}}{q_j})} \\ \mathrm{{ + }}D_{1i}^{{\omega _{\mathrm{{y1}}}}}{\omega _{\mathrm{{y1}}}} + D_{2i}^{{\omega _{\mathrm{{y1}}}}}{\alpha _2} + D_{3i}^{{\omega _{\mathrm{{y1}}}}}{\delta _{{\omega _{\mathrm{{y1}}}}}} + D_{3i}^{''{\omega _{\mathrm{{y1}}}}}{{\ddot{\delta }}_{{\omega _{\mathrm{{y1}}}}}}\\ + \sum \limits _p^{} {(G_{ip}^{''{\omega _{\mathrm{{y1}}}}}\Delta {{\ddot{z}}_p} + G_{ip}^{{\omega _{\mathrm{{y1}}}}}\Delta {z_p})} + \sum \limits _j^{} {(R_{ij}^{'{\omega _{\mathrm{{y1}}}}}{{\dot{q}}_j} + R_{ij}^{{\omega _{\mathrm{{y1}}}}}{q_j})} \\ + D_{1i}^{{\omega _{\mathrm{{x1}}}}}{\omega _{\mathrm{{y1}}}} + D_{2i}^{{\omega _{\mathrm{{y1}}}}}{\alpha _1} + D_{3i}^{{\omega _{\mathrm{{x1}}}}}{\delta _{{\omega _{\mathrm{{x1}}}}}} + D_{3i}^{''{\omega _{\mathrm{{x1}}}}}{{\ddot{\delta }}_{{\omega _{\mathrm{{x1}}}}}}\\ + {{\bar{Q}}_{xi}} + {{\bar{Q}}_{yi}} + {{\bar{Q}}_{zi}}, \end{array} \end{aligned}$$

(2.7)

where $\xi _i$ is the i-order elastic damping, ${\varpi _i}$is the i-order elastic frequency. $\Delta z_p$ is the p-th order transverse sloshing displacement. $\delta _{\omega _{x1}}$, ${\delta }_{\omega _{y1}}$, $\delta _{\omega _{z1}}$ are the engine swing angles, $G_{ip}^{\prime \prime \omega _{z1}}$, $G_{ip}^{\omega _{z1}}$, $G_{ip}^{\prime \prime \omega _{y1}}$, $G_{ip}^{\omega _{y1}}$ are the coupling coefficients of the p-th order sloshing to the i-th order elasticity, $R_{ij}^{\prime \omega _{z1}}$, $R_{ij}^{\omega _{z1}}$, $R_{ij}^{\prime \omega _{y1}}$, $R_{ij}^{\omega _{y1}}$ are the coupling coefficients of the j-th order to the i-th order elasticity, ${\bar{Q}}_{xi}$, ${\bar{Q}}_{yi}$, ${\bar{Q}}_{zi}$ are the elastic generalized disturbances.

The motion equation describing normal sloshing is

$$\begin{aligned} \begin{array}{l} \Delta {{\ddot{y}}_p} + 2{\zeta _{hp}}{\Omega _p}\Delta {{\dot{y}}_p} + \Omega _p^2\Delta {y_p} = \\ - {E_1}\Delta \dot{\theta }+ {E_2}\Delta \varphi + {E_3}\Delta \alpha - {E_{pz}}\Delta \ddot{\varphi }+ \sum \limits _i^{} {({{E''}_{ip}}{{\ddot{q}}_{iy}} + {E_{ip}}{q_{iy}})}, \end{array} \end{aligned}$$

(2.8)

where $E''_{ip}$, $E_{ip}$ are the elastic hinge coupling coefficients, ${\zeta _{hp}}$ is the i-th order sloshing damping, ${\Omega _p}$ is the p-th order sloshing frequency.

2.2.2 Constraints and Objectives

(1) Initial state constraints

The takeoff time $t_0$ is defined as the initial time. The initial position at $t_0$ is the location of the launch point, the initial velocity is that of the launch point generated by the earth’s rotation, and the liftoff mass is the initial mass. The rocket flies vertically off the launch pad, and the initial state constraints can be expressed as

$$\begin{aligned} \begin{array}{*{20}{c}} {\left[ {\boldsymbol{r},\boldsymbol{V},m} \right] \left( {{t_0}} \right) = \left[ {{\boldsymbol{r}_0},{\boldsymbol{V}_0},{m_0}} \right] ,}&{\varphi = {{90}^ \circ },}&{\psi = {0^ \circ },} \end{array} \end{aligned}$$

(2.9)

where $\phi$, $\psi$ are the pitch and yaw angles, respectively.

(2) Process constraints

When flying in the atmosphere, the following constraints should be met to ensure structural safety:

$$\begin{aligned} \begin{array}{c} {\left| {q\alpha } \right| \le q{\alpha _{\max }},}\quad {N \le {N_{\max }},}\quad {q < {q_{\max }},} \end{array} \end{aligned}$$

(2.10)

where N is the overload, $\alpha$ is the angle of attack (AOA). The subscripts max and min represent the maximum and minimum values of the corresponding constraints, respectively.

Limited by the control ability of the actuators, the following constraints are prescribed:

$$\begin{aligned} \begin{array}{c} {\left| \delta \right| \le {\delta _{\max }},} \quad {MH \le M{H_{\max }},} \end{array} \end{aligned}$$

(2.11)

where $\delta$ is the engine swing angle, and MH is the hinge moment. To ensure the attitude stability, the following constraints are imposed:

$$\begin{aligned} \begin{array}{l} \left| {{\omega _\varphi }} \right| ,\left| {{\omega _\psi }} \right| \le {\omega _{\max }},\;{\varphi _{\min }} \le \varphi \le {\varphi _{\max }},\;{\psi _{\min }} \le \psi \le {\psi _{\max }},\\ {\boldsymbol{u}_T}\left( t \right) = {\left[ {0,1,0} \right] ^T},\;t \in \left[ {{t_0},{t_1}} \right] , \end{array} \end{aligned}$$

(2.12)

where $\omega _\phi$, $\omega _\psi$ are the corresponding angular velocities, $\boldsymbol{u}_T$ is the thrust direction.

The rocket should keep rising vertically for a short time ($t_1$) after takeoff, that is, $\boldsymbol{u}_T$ is perpendicular to the horizontal plane.

According to the engine configurations, the mass differential equation given by Eq. (2.1) is revised to the following equation, where the equivalent thrust and specific impulse of the k-stage engines are denoted by the superscript k:

$$\begin{aligned} {\dot{m}^k} = - \frac{{\left( {\left\| {{\boldsymbol{F}}^k _T} \right\| - S_e^k\left( {P_e^k - P_e^k} \right) } \right) }}{{I_{sp}^k{g_0}}}. \end{aligned}$$

(2.13)

For the multi-stage launcher, the states of the velocity, position, and attitude between the stages are continuous. During stage separations, the mass constraints are included:

$$\begin{aligned} \begin{array}{cc} {{{\left[ {\begin{array}{cccc} {{\boldsymbol{r}_0},}&{{\boldsymbol{V}_0},}&{{\varphi _0},}&{{\psi _0}} \end{array}} \right] }^k} = {{\left[ {\begin{array}{*{20}{c}} {{\boldsymbol{r}_f},}&{{\boldsymbol{V}_f},}&{{\varphi _f},}&{{\psi _f}} \end{array}} \right] }^{k - 1}},}&{m_0^k = m_f^{k - 1} - m_s^{k - 1},} \end{array} \end{aligned}$$

(2.14)

where $m_s$ is the separation mass, and the subscript f represents the terminal state of each stage.

(3) Terminal constraints

When the payload is released from the launcher, it would enter into an orbit, which is determined by the terminal states of the payload, the gravitational force, and other perturbation forces. If only considering the gravitational effect, the OEs can be calculated based on $V_x$, $V_y$, $V_z$, and x, y, z in the LICS.

First, we have the following equation:

$$\begin{aligned} \begin{array}{l} \begin{array}{ccc} {{x_r} = x + {R_{0x}},}&{}{{y_r} = y + {R_{0y}},}&{}{{z_r} = z + {R_{0z}},} \end{array}\\ \begin{array}{cc} {r = \sqrt{x_r^2 + y_r^2 + z_r^2} ,}&{}{V = \sqrt{V_x^2 + V_y^2 + V_z^2} ,} \end{array} \end{array} \end{aligned}$$

(2.15)

where $V_x$, $V_y$, $V_z$ are the velocity components in LICS, and x, y, z are the position components in LICS, $R_{0x}$, $R_{0y}$, $R_{0z}$ are the geocentric vector components to the launch point.

Then, the OEs are

$$\begin{aligned} \begin{array}{cc} {a = \frac{r}{{2 - \upsilon }},}&{\upsilon = \frac{{r{V^2}}}{{\mu }},} \end{array} \end{aligned}$$

(2.16)

$$\begin{aligned} \begin{array}{cc} {e = \sqrt{1 - \left( {2 - \upsilon } \right) \upsilon {{\cos }^2}\gamma } ,}&{\gamma = \arcsin \frac{{{V_x}{x_r} + {V_y}{y_r} + {V_z}{z_r}}}{{Vr}},} \end{array} \end{aligned}$$

(2.17)

$$\begin{aligned} \begin{array}{cccc} {{h_p} = {r_p} - {R_e},}&{{r_p} = a\left( {1 - e} \right) ,}&{{h_a} = {r_a} - {R_e},}&{{r_a} = a\left( {1 - e} \right) ,} \end{array} \end{aligned}$$

(2.18)

where $R_e$ is the radius of the Earth; $r_p$, $r_a$ are the distances from the center of the Earth to perigee and apogee, respectively; $\mu$ is the gravitational constant.

$$\begin{aligned} T = 2\pi \sqrt{\frac{{{a^3}}}{{\mu }}} , \end{aligned}$$

(2.19)

where T is orbital period.

The parameters characterizing the orbital direction are i, $\Omega$, and $\omega$:

$$\begin{aligned} \begin{array}{ccc} {i = \arccos \frac{{{h_z}}}{h},}&{}{\left[ \begin{array}{l} {h_x}\\ {h_y}\\ {h_z} \end{array} \right] = \left[ \begin{array}{l} y{V_z} - z{V_y}\\ z{V_x} - x{V_z}\\ x{V_y} - y{V_x} \end{array} \right] ,}&{h = \sqrt{h_x^2 + h_y^2 + h_z^2} ,} \end{array} \end{aligned}$$

(2.20)

where $[h_x, h_y, h_z]^T$ is the vector product of velocity and position.

$$\begin{aligned} \begin{array}{cc} {\sin \Omega = \frac{{{h_x}}}{{\sqrt{h_x^2 + h_y^2} }},}&{\cos \Omega = - \frac{{{h_y}}}{{\sqrt{h_x^2 + h_y^2} }},} \end{array} \end{aligned}$$

(2.21)

where $\Omega \in [0,2\pi ]$, and the quadrant is determined according to the symbols of $\sin \Omega$ and $\cos \Omega$. Furthermore,

$$\begin{aligned} w = u - f, \end{aligned}$$

(2.22)

where f is the true anomaly, u is the angular argument to the ascending node and calculated by the following equation:

$$\begin{aligned} u = \left\{ \begin{array}{l} \begin{array}{cccc} {\arccos \frac{{{x_r}\cos \Omega + {y_r}\sin \Omega }}{r},}&{}{}&{}{}&{}{} \end{array}({z_r} \ge 0)\\ 2\pi - \arccos \frac{{{x_r}\cos \Omega + {y_r}\sin \Omega }}{r},\begin{array}{*{20}{c}} {}&{}{} \end{array}({z_r} < 0) \end{array} \right. , \end{aligned}$$

(2.23)

f is used to characterize the position of the payload in orbit and is expressed as follows:

$$\begin{aligned} f = \left\{ \begin{array}{l} \arccos \frac{{a\left( {1 - {e^2}} \right) - r}}{{er}},\begin{array}{*{20}{c}} {}&{}{}&{}{} \end{array}(\gamma \ge 0)\\ \begin{array}{cc} {2\pi - \arccos \frac{{a\left( {1 - {e^2}} \right) - r}}{{er}},}&{}{} \end{array}(\gamma < 0) \end{array} \right. . \end{aligned}$$

(2.24)

The terminal velocity and position are transformed into constraints of the OEs, as well as a terminal mass constraint, shown as follows:

$$\begin{aligned} \begin{array}{l} \left\| {{{\left[ {{a_s},{} {} {} {e_s},{} {} {} {i_s},{} {} {} {\Omega _s},{} {} {} {w_s},{} {} {} {f_s}} \right] }^T} - {{\left[ {a,{} {} {} e,{} {} {} i,{} {} {} \Omega ,{} {} {} w,{} {} {} f} \right] }^T}\left( {{t_s}} \right) } \right\| \le \Delta Orbit,\\ m\left( {{t_s}} \right) \le {m_{allow}}, \end{array} \end{aligned}$$

(2.25)

where $t_s$ is the terminal time and the subscript s represents the nominal state at the departure time. $\Delta Orbit$ is the maximum allowance of the six orbital elements, $m_{allow}$ is the minimum allowable mass at the end of the ascent phase.

(4) Objectives

The objective of the ascent guidance method of a launcher can be expressed as the weighted sum of maximizing the residual mass at the payload departure time while minimizing the terminal state deviations:

$$\begin{aligned} \min \mathrm{{ }}J = - m\left( {{t_s}} \right) + {\lambda _{orbit}}\left\| {{{\left[ {{a_s}, {e_s}, {i_s}, {\Omega _s}, {w_s}, {f_s}} \right] }^T} - {{\left[ {a, e, i, \Omega , w, f} \right] }^T}\left( {{t_s}} \right) } \right\| , \end{aligned}$$

(2.26)

where $\lambda _{orbit}$ is the weight of the terminal state deviations.

In addition to ensuring a stable flight, the peak value of the hinge torque and the peak power consumption of the servomechanisms need to be minimized:

$$\begin{aligned} \min J = {\lambda _{MH}}\left| {MH} \right| + {\lambda _{sv}}\int _0^{{t_f}} {\left| {MH \times {\omega _{sv}}} \right| } dt. \end{aligned}$$

(2.27)

where ${\lambda _{MH}}$, ${\lambda _{sv}}$ are the weight coefficients, $\omega _{sv}$ is the angular velocity of servomechanisms.

This section constructs a complete motion model of a launch vehicle. It should be pointed out that the tracking guidance is still used when flying in the atmosphere, so the variables related to aerodynamics are interpolated according to the parameters of the nominal trajectory. The exo-atmospheric guidance methods are the focuses of the following discussion, and the rotational equations are not included in the AGMs due to the assumption that the attitude control can track the guidance commands well.

2.3 Exo-Atmospheric Analytical Guidance Methods

2.3.1 Basic Closed-Loop Guidance Method for Long March Launch Vehicles (LMLVs)

• The process of CLG

A closed-loop guidance method for LMLVs in a vacuum environment is summarized as follows.

Step 1: Release the expectation of the fixed-point injection, and take five OEs directly as terminal constraints.

Step 2: Find the most matching entry point according to the current state of the launcher.

The state includes the velocity, position, mass, specific impulse, and mass flow rate. The time-to-go and entry point are solved iteratively based on the above parameters, and the entry point is updated in each guidance cycle.

Step 3: Construct an optimization problem of the current guidance cycle in the orbital coordinate system (OCS).

The main features of this optimization problem are as follows:

• 1. The objective function is to minimize the fuel consumption;

• 2. The OE constraints are transformed into the state variables after an optimal entry point is found;

• 3. The terminal constraints in the OCS are further simplified, and only the velocity along the $o\xi$ axis and the position along the $o\eta$ axis are non-zero.

• 4. Make the following conversion:

  $$\begin{aligned} {\dot{W}_{x1}}(t) = \frac{{{P_{x1}}}}{{m(t)}} = \frac{{{I_{sp}} \cdot \dot{m}}}{{{m_0} - \dot{m}t}} = \frac{I_{sp}}{{\tau - t}}, \end{aligned}$$

  (2.28)

  where $P_{x1}$ is the axial thrust, $m_0$ is the initial mass, and $\dot{m}$ is the mass-flow rate.

  In this way, $\dot{W}_{x1}(t)$ is related to $I_{sp}$ and the mass flow ratio $\tau = {{{m_0}} / {\dot{m}}}$, rather than the parameters that are difficult to measure in real time, such as $P_{x1}$, $m_0$, and $\dot{m}$. It should be noted that $\tau$ can be determined by $\dot{W}_{x1}(0)$, then the analytical expression of $\dot{W}_{x1}(t)$ can be obtained.

• 5. Design an analytic expression to represent the thrust direction, i.e., the pitch and yaw commands.

  Many simulations have shown that the optimal thrust direction in a vacuum environment can be approximated as a linear function of time, as follows:

  $$\begin{aligned} \left\{ \begin{array}{l} {\varphi _{cx}}\left( t \right) = \tilde{\varphi }+ \left( { - {k_1} + {k_2} \cdot t} \right) \\ {\psi _{cx}}\left( t \right) = \tilde{\psi }+ \left( { - {k_3} + {k_4} \cdot t} \right) \end{array} \right. . \end{aligned}$$

  (2.29)

• 6. Solve for the unknown variables in Eq. (2.29) based on the terminal velocity and position constraints, then obtain the guidance command of the current cycle for the real-time control.

Step 4: Repeat Steps 2 and 3 during each guidance cycle until the cutoff equations are met to shut down the engines.

The CLG is also known as the iterative guidance mode (IGM). The above processing assumes that the PTO lies within the performance scope of the launcher, so we can always find a matching entry point on the PTO, and the optimization problem is converted to the planning of fixed-point terminal constraints in each guidance cycle. In the following cycle, the entry point shall be updated again.

The CLG has the following advantages over the PGMs:

• 1. High injection accuracy. It predicts and regulates the entry point responsively, mostly matching the states of the launcher and guaranteeing that all OEs are met. The initial states, terminal constraints, and performance indices rather than a reference trajectory are considered in the real-time planning, allowing deviations from the prescribed flight path to counter interferences. On the contrary, PGMs can only satisfy few constraints or synthesized objectives, flying nearby the nominal trajectory.

• 2. Robust to thrust variations. This is due to its sensitivity to the change of the thrust, and the flight path would be re-planned in line with the variations.

• 3. Responsive to the target orbit adjustment. If the target is re-scheduled just before liftoff, only the new OEs need to be uploaded to the OBC, avoiding the hard work of the reference trajectory preparation and guide coefficients tuning.

• The solutions of the guidance law variables

Seven parameters in the guidance law of Eq. (2.29), i.e., $\tilde{\phi }$, $\tilde{\psi }$, $k_1$, $\sim$, $k_4$, and t, need to be solved. Note that t represents the time-to-go, also denoted as $T_k$. The CLG is adopted when the rocket flies out of the atmosphere, so only the thrust and gravity are considered as the external forces, and the aerodynamic drag is omitted, which makes the following analytical solution possible.

The OCS is labeled as ${O_E} - \xi \eta \zeta$, where ${O_E}\eta$ points from the center of the earth to the injection point, $\xi {O_E}\eta$ denotes the orbital plan, and the three coordinate axes follow the right-hand rule, as shown in Fig. 2.2.

Fig. 2.2

Definition of thrust vector direction

Consider that the OEs are set as the terminal constraints and the flight has been out of the atmosphere, the planning problem described in Sect. 2.2 is revised in the OCS as follows:

$$\begin{aligned} \begin{array}{cc} \mathrm{{Objective:}}&{J = \int _0^{{T_k}} {d\tilde{t}} = {T_k},} \end{array} \end{aligned}$$

(2.30)

$$\begin{aligned} \begin{array}{l} Dynamics: \dot{\boldsymbol{X}} = \boldsymbol{f}(\boldsymbol{X},\boldsymbol{u},\tilde{t}),\\ \begin{array}{cc} {\begin{array}{ccccccccccccccc} {}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{}&{}{} \end{array}}&{}{} \end{array}or\left\{ \begin{array}{l} {{\dot{V}}_\xi }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \cos {\varphi ^*}(\tilde{t}) \cdot \cos {\psi ^*}(\tilde{t}) + {g_\xi }(\tilde{t})\\ {{\dot{V}}_\eta }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin {\varphi ^*}(\tilde{t}) \cdot \cos {\psi ^*}(\tilde{t}) + {g_\eta }(\tilde{t})\\ {{\dot{V}}_\zeta }(\tilde{t}) = - {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin {\psi ^*}(\tilde{t}) + {g_\zeta }(\tilde{t})\\ \dot{\xi }(\tilde{t}) = {V_\xi }(\tilde{t})\\ \dot{\eta }(\tilde{t}) = {V_\eta }(\tilde{t})\\ \dot{\zeta }(\tilde{t}) = {V_\zeta }(\tilde{t}) \end{array} \right. , \end{array} \end{aligned}$$

(2.31)

Constraints:

$$\begin{aligned} {\boldsymbol{X}} = {\left[ {\begin{array}{cccccc} {{V_{\xi 0}}}&{{V_{\eta 0}}}&{{V_{\zeta 0}}}&{{\xi _0}}&{{\eta _0}}&{{\zeta _0}} \end{array}} \right] ^T}, \end{aligned}$$

(2.32)

$$\begin{aligned} {N_1}\left( {\boldsymbol{X}\left( {{T_k}} \right) ,{T_k}} \right) = 0. \end{aligned}$$

(2.33)

The performance index, Eq. (2.30), is fuel-efficient and can also be expressed as the shortest time for the liquid launcher considering a basically constant thrust and mass flow rate. Equation (2.32) is the initial condition, and Eq. (2.33) represents the terminal constraints, i.e., the target orbital elements.

The control variables are the directions of the thrust vectors, which can be expressed by the Euler angles, ${\phi _{cx}}$ and ${\psi _{cx}}$, as follows:

$$\begin{aligned} \boldsymbol{u} = [{\phi _{cx}}(t),{\psi _{cx}}(t)]. \end{aligned}$$

(2.34)

Hypothesis 1: A uniform gravitational field is introduced to simplify the state equations, i.e., the gravity is expressed by the average of the gravity of the current and entry point (the selection of the entry point will be introduced later):

$$\begin{aligned} \left\{ \begin{array}{l} {g_\xi }(\tilde{t}) = {{\bar{g}}_\xi }\\ {g_\eta }(\tilde{t}) = {{\bar{g}}_\eta }\\ {g_\zeta }(\tilde{t}) = {{\bar{g}}_\zeta } \end{array} \right. . \end{aligned}$$

(2.35)

The following Hamiltonian function is established:

$$\begin{aligned} \begin{array}{l} H = 1 + {{\mathbf {\lambda }}^t}\boldsymbol{f} = 1 + {\lambda _{V\xi }}({{\dot{W}}_{x1}}\cos {\phi ^*}\cos {\psi ^*} + {{\bar{g}}_\xi }) \\ \;\;\;\, + {\lambda _{V\eta }}({{\dot{W}}_{x1}}\sin {\phi ^*}\cos {\psi ^*} + {{\bar{g}}_\eta }) + {\lambda _{V\zeta }}( - {{\dot{W}}_{x1}}\sin {\psi ^*} \\ \;\;\;\, + {{\bar{g}}_\zeta }) + {\lambda _\xi }{V_\xi } + {\lambda _\eta }{V_\eta } + {\lambda _\zeta }{V_\zeta }. \end{array} \end{aligned}$$

(2.36)

To maximize the Hamiltonian function Eq. (2.36), the following conditions should be met:

$$\begin{aligned} \frac{{\partial H}}{{\partial {\phi ^*}}} = {\dot{W}_{x1}}\cos {\psi ^*}\left( { - {\lambda _{V\xi }}\sin {\phi ^*} + {\lambda _{V\eta }}\cos {\phi ^*}} \right) = 0, \end{aligned}$$

(2.37)

$$\begin{aligned} \frac{{\partial H}}{{\partial {\psi ^*}}} = {\dot{W}_{x1}}\left( { - {\lambda _{V\xi }}\cos {\phi ^*}\sin {\psi ^*} - {\lambda _{V\eta }}\sin {\phi ^*}\sin {\psi ^*} - {\lambda _{V\zeta }}\cos {\psi ^*}} \right) = 0. \end{aligned}$$

(2.38)

By solving the above equations, we obtain the following equations:

$$\begin{aligned} {\phi ^*} = \arctan \frac{{{\lambda _{V\eta }}}}{{{\lambda _{V\xi }}}}, \end{aligned}$$

(2.39)

$$\begin{aligned} {\psi ^*} = - \arctan \frac{{{\lambda _{V\zeta }}}}{{{\lambda _{V\xi }}}}\cos {\phi ^*}. \end{aligned}$$

(2.40)

The adjoint equations are as follows:

$$\begin{aligned} \begin{array}{l} \begin{array}{ccc} {{{\dot{\lambda }}_{V\xi }} = - \frac{{\partial H}}{{\partial {V_\xi }}} = - {\lambda _\xi },}&{}{{{\dot{\lambda }}_{V\eta }} = - \frac{{\partial H}}{{\partial {V_\mu }}} = - {\lambda _\eta },}&{}{{{\dot{\lambda }}_{V\zeta }} = - \frac{{\partial H}}{{\partial {V_\zeta }}} = - {\lambda _\zeta },} \end{array}\\ \begin{array}{ccc} {{{\dot{\lambda }}_\xi } = - \frac{{\partial H}}{{\partial \xi }} = 0,}&{}{{{\dot{\lambda }}_\eta } = - \frac{{\partial H}}{{\partial \eta }} = 0,}&{}{{{\dot{\lambda }}_\zeta } = - \frac{{\partial H}}{{\partial \zeta }} = 0.} \end{array} \end{array} \end{aligned}$$

(2.41)

The following solution is derived from Eq. (2.41):

$$\begin{aligned} \begin{array}{l} \begin{array}{ccc} {{\lambda _{V\xi }} = {\lambda _{V\xi 0}} - {\lambda _\xi }\tilde{t},}&{}{{\lambda _{V\eta }} = {\lambda _{V\eta 0}} - {\lambda _\eta }\tilde{t},}&{}{{\lambda _{V\zeta }} = {\lambda _{V\zeta 0}} - {\lambda _\zeta }\tilde{t},} \end{array}\\ \begin{array}{ccc} {{\lambda _\xi } = {\lambda _{\xi 0}},}&{}{{\lambda _\eta } = {\lambda _{\eta 0}},}&{}{{\lambda _\zeta } = {\lambda _{\zeta 0}}.} \end{array} \end{array} \end{aligned}$$

(2.42)

(1) First, only the velocity constraints are considered.

If only the terminal velocity constraints are considered and the terminal position constraints are relaxed, then

$$\begin{aligned} {\lambda _\xi } = {\lambda _\eta } = {\lambda _\zeta } = 0. \end{aligned}$$

(2.43)

Substituting Eqs. (2.43) and (2.42) into Eqs. (2.39) and (2.40), we obtain the optimal solutions of the control variables:

$$\begin{aligned} {\phi ^*} = \arctan \frac{{{\lambda _{V\eta 0}}}}{{{\lambda _{V\xi 0}}}} = \tilde{\phi }, \end{aligned}$$

(2.44)

$$\begin{aligned} {\psi ^*} = - \arctan \frac{{{\lambda _{V\zeta 0}}}}{{{\lambda _{V\xi 0}}}}\cos \tilde{\phi }= \tilde{\psi }. \end{aligned}$$

(2.45)

Thus, an important conclusion is drawn: the optimal control variables are constant if only the velocity constraints are taken into account. To determine this constant, we substitute Eqs. (2.44) and (2.45) into the first three terms of state equations given by Eq. (2.31):

$$\begin{aligned} \left\{ \begin{array}{l} {{\dot{V}}_\xi }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \cos \tilde{\varphi }\cdot \cos \tilde{\psi }+ {{\bar{g}}_\xi }\\ {{\dot{V}}_\eta }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin \tilde{\varphi }\cdot \cos \tilde{\psi }+ {{\bar{g}}_\eta }\\ {{\dot{V}}_\zeta }(\tilde{t}) = - {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin \tilde{\psi }+ {{\bar{g}}_\zeta } \end{array} \right. . \end{aligned}$$

(2.46)

Assuming that the time-to-go, $T_k$, and the entry point are known, so the terminal velocity and position constraints are determined, then $\tilde{\phi }$ and $\tilde{\psi }$ can be obtained by integration:

$$\begin{aligned} \left\{ \begin{array}{l} {V_{\xi k}} - {V_{\xi 0}} = L \cdot \cos \tilde{\phi }\cdot \cos \tilde{\psi }+ {{\bar{g}}_\xi } \cdot {T_k}\\ {V_{\eta k}} - {V_{\eta 0}} = L \cdot \sin \tilde{\phi }\cdot \cos \tilde{\psi }+ {{\bar{g}}_\eta } \cdot {T_k}\\ {V_{\zeta k}} - {V_{\zeta 0}} = - L \cdot \sin \tilde{\psi }+ {{\bar{g}}_\zeta } \cdot {T_k} \end{array} \right. , \end{aligned}$$

(2.47)

where $L = \int _0^{{T_k}} {{{\dot{W}}_{x1}}d\tilde{t}}$. Then,

$$\begin{aligned} \tilde{\phi }= \arctan \frac{{{V_{\eta k}} - {V_{\eta 0}} - {{\bar{g}}_\eta } \cdot {T_k}}}{{{V_{\xi k}} - {V_{\xi 0}} - {{\bar{g}}_\xi } \cdot {T_k}}}, \end{aligned}$$

(2.48)

$$\begin{aligned} \tilde{\psi }= \arcsin \frac{{ - {V_{\zeta k}} + {V_{\zeta 0}} + {{\bar{g}}_\zeta } \cdot {T_k}}}{L}. \end{aligned}$$

(2.49)

$$\begin{aligned} L = \int _0^{{T_k}} {{{\dot{W}}_{x1}}d\tilde{t}} = \int _0^{{T_k}} {\frac{I_{sp}}{{\tau - \tilde{t}}}d\tilde{t} = } {I_{sp}} \cdot \ln \frac{\tau }{{\tau - {T_k}}}. \end{aligned}$$

(2.50)

Hypothesis 2: For the guidance law of Eq. (2.29), $\tilde{\phi }$ and $\tilde{\psi }$ are used to ensure the terminal velocity conditions, and they are determined by Eqs. (2.48) and (2.49), respectively. The expressions $( - {k_1} + {k_2} \cdot \tilde{t})$ and $( - {k_3} + {k_4} \cdot \tilde{t})$ could be used to meet the terminal position conditions.

(2) Second, the position constraints are also included.

Thus the expressions of Eqs. (2.44), (2.45) are updated as follows:

$$\begin{aligned} \begin{array}{cc} {{\phi ^\mathrm{{*}}} = \tilde{\phi }- {k_1} + {k_2}t,}&{{\psi ^\mathrm{{*}}} = \tilde{\psi }- {k_3} + {k_4}t} \end{array} \end{aligned}$$

(2.51)

Based on the known entry point, the terminal conditions can be transformed into the following:

$$\begin{aligned} \boldsymbol{X}\left( {{T_k}} \right) = \left[ \begin{array}{l} {V_{\xi k}}\\ {V_{\eta k}}\\ {V_{\zeta k}}\\ {\xi _k}\\ {\eta _k}\\ {\zeta _k} \end{array} \right] = \left[ \begin{array}{l} {V_k} \cdot \cos {\theta _k}\\ {V_k} \cdot \sin {\theta _k}\\ 0\\ 0\\ {R_k}\\ 0 \end{array} \right] , \end{aligned}$$

(2.52)

where ${V_k}$ is the required injection velocity, ${\theta _k}$ is the terminal velocity inclination, and ${R_k}$ is the terminal geocentric vector diameter.

The state equation is converted to the following form:

$$\begin{aligned} \left\{ \begin{array}{l} \ddot{\xi }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \cos {\varphi ^*}(\tilde{t}) \cdot \cos {\psi ^*}(\tilde{t}) + {{\bar{g}}_\xi }\\ \ddot{\eta }(\tilde{t}) = {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin {\varphi ^*}(\tilde{t}) \cdot \cos {\psi ^*}(\tilde{t}) + {{\bar{g}}_\eta }\\ \ddot{\zeta }(\tilde{t}) = - {{\dot{W}}_{x1}}(\tilde{t}) \cdot \sin {\psi ^*}(\tilde{t}) + {{\bar{g}}_\zeta } \end{array} \right. . \end{aligned}$$

(2.53)

If $( - {k_1} + {k_2} \cdot \tilde{t})$ and $( - {k_3} + {k_4} \cdot \tilde{t})$ are small quantities, then

$$\begin{aligned} \begin{array}{l} \cos {k_i} \approx 1,\\ \sin {k_i} \approx {k_i},\\ \cos {\phi ^*} = \cos \tilde{\phi }+ {k_1}\sin \tilde{\phi }- {k_2}\tilde{t}\sin \tilde{\phi },\\ \sin {\phi ^*} = \sin \tilde{\phi }- {k_1}\cos \tilde{\phi }+ {k_2}\tilde{t}\cos \tilde{\phi },\\ \cos {\psi ^*} = \cos \tilde{\psi }+ {k_3}\sin \tilde{\psi }- {k_4}\tilde{t}\sin \tilde{\psi },\\ \sin {\psi ^*} = \sin \tilde{\psi }- {k_3}\cos \tilde{\psi }+ {k_4}\tilde{t}\cos \tilde{\psi }. \end{array} \end{aligned}$$

(2.54)

The expressions $( - {k_1} + {k_2} \cdot \tilde{t})$ and $( - {k_3} + {k_4} \cdot \tilde{t})$ are required not to have apparent effects on the terminal velocity, so

$$\begin{aligned} \begin{array}{c} {\int _0^{{t_k}} {( - {k_1} + {k_2} \cdot t)dt} = 0,} \end{array} \end{aligned}$$

(2.55)

$$\begin{aligned} \begin{array}{c} {\int _0^{{t_k}} {( - {k_3} + {k_4} \cdot t)dt} = 0.} \end{array} \end{aligned}$$

(2.56)

The longitudinal position is mainly determined by $T_k$. Thus the transverse and normal position constraints are:

$$\begin{aligned} \begin{array}{c} {\eta _k} = \eta + {v_\eta } \cdot {t_k} + \int _0^{{t_k}} {\int _0^t {\ddot{\eta }(\tilde{t})} dtdt} , \end{array} \end{aligned}$$

(2.57)

$$\begin{aligned} \begin{array}{c} {\zeta _k} = \zeta + {v_\zeta } \cdot {t_k} + \int _0^{{t_k}} {\int _0^t {\ddot{\zeta }(\tilde{t})} dtdt} . \end{array} \end{aligned}$$

(2.58)

The four equations, i.e., Eqs. (2.55)–(2.58), are used to solve $k_1 \sim k_4$. The integral processes are not complicated that the derivation is omitted, and interested readers can refer to [37].

(3) Finally, the time-to-go and the entry point are solved based on the geocentric angle.

${T_k}$, the latest time-to-go, would be solved with the optimal entry point concurrently. This process is illustrated in Fig. 2.3.

Fig. 2.3

Solving of optimal entry point

$P_0$ is the current position of the launcher. The terminal position $P_f$ can be predicted according to the CLG command planned in the current cycle. According to the geocentric angle between $P_f$ and the ascending node ${\Phi _0} + \Delta \Phi$, the position ${O_f}$ on the target orbit can be determined with the same geocentric angle. If the velocities of ${P_f}$ and ${O_f}$ are the same, ${O_f}$ is then regarded as the latest entry point, and ${T_k}$ needs no compensation; otherwise, a correction time $\Delta t$ should be found to ensure the new predicted terminal position after ${T_k} + \Delta t$ is located in the PTO, as shown as $O_f^*$ in Fig. 2.3. $O_f^*$ is also considered to be a new entry point.

According to the above analysis, $T_k$ is updated by the following process:

$$\begin{aligned} {v_0} + L({T_k}) + \tilde{g}({T_k} + \Delta t) + \frac{{\partial L}}{{\partial t}} \cdot \Delta t = f_v(\mathbf{{S}}) + \frac{{\partial f_v(\mathbf{{S}})}}{{\partial t}} \cdot \Delta t, \end{aligned}$$

(2.59)

$$\begin{aligned} {T_k} \leftarrow {T_k} + \Delta t, \end{aligned}$$

(2.60)

where ${v_0}$ is the current velocity of the rocket, $L({T_k})$ denotes the apparent velocity increment, $\tilde{g}({T_k} + \Delta t)$ represents the gravitational effects on the velocity, $f_v$ denotes the velocity of position $\boldsymbol{S}$ on the PTO, and $\boldsymbol{S}$ has the same geocentric angle as the predicted terminal position of the launcher.

After $T_k$ converges to a stable value during the iteration process, the orbit entry point, $O_f^*$, is also determined. Thus the terminal velocity and position are known, which are used by Eqs. (2.35), (2.48), (2.49), (2.57), (2.58).

At this point, all the variables in Eq. (2.29) have been solved, and the guidance law is then updated and applied for current control. The above solving process is carried out iteratively in each guidance cycle.

In the above treatment, some approximates are made, which would produce deviations. However, as the rocket approaches the entry point, the accuracy of the above processing is also continuously improved. If the flight arc is long, the gravitational effect can be processed in segments, or a high-order approximation can be substituted.

The CLG is very sensitive to thrust variations, including thrust drops. Thus, it has a certain fault-tolerance ability by adjusting the flight path in time. When performing trajectory planning at fault time $t_d$ and taking $t_d$ as the start time of the following flight, we obtain

$$\begin{aligned} {\dot{W}_{x1}}({t_d}) = \frac{I_{sp}}{{\tau ({t_d})}},\;\mathrm{{i}}\mathrm{{.e}}\mathrm{{.}},\;\tau ({t_d}) = \frac{I_{sp}}{{{{\dot{W}}_{x1}}({t_d})}}. \end{aligned}$$

(2.61)

That is, $\tau (t_d)$ is updated during each planning cycle according to the apparent acceleration ${\dot{W}_{x1}}({t_d})$ measured by the IMU. Then, the dropped thrust is reflected in the apparent acceleration, which causes $\tau (t_d)$ to increase. Under the assumption that ${I_{sp}}$ and $T_k$ remain unchanged, L decreases according to Eq. (2.50), so $\Delta t$ increases therefrom according to Eq. (2.59), and then $T_k$ increases. This means that the flight time is extended and the orbit entry point is re-determined.

An example of LM-7 is given to illustrate IGM’s adaptability to thrust variations. The engines of its second stage start up with a thrust of 150 kN, and then are tuned to 180 kN within 7 s. Four failure modes are considered, and the guidance commands (the pitch Euler angles) are compared with those under nominal conditions, as shown in Fig. 2.4, where the guidance commands are all re-planned after the failure occurs. However, the premise of the fault tolerance is that there is sufficient remaining performance to reach the PTO, and the measures if the performance is greatly degraded are discussed in Sect. 2.4.

Fig. 2.4

Adaptability of CLG to thrust reduction

Nowadays, many enhanced algorithms have evolved from this basic method. The improvements are mainly concentrated in Step 3 of Sect. 2.3.1, i.e., revising the form of the thrust directions or correcting the terminal velocity and position constraints. These upgraded versions of CLGs are discussed in the following sections.

2.3.2 Evolutions of the Closed-Loop Guidance Methods

The evolution methods provide acceptable suboptimal solutions under more complicated scenarios or constraints, which are proved to be feasible in real flights.

2.3.2.1 IGM Across Different Flight Phases

The above discussion only considers single powered flight phase. However, the IGM is not always applied in the last stage. The earlier the IGM is introduced, the more robust it is to faults.

During planning, the accelerations of the next stages need to be integrated to obtain the terminal states, so the algorithm’s complexity is closely related to the number of stages or segments, and each additional segment will require additional calculations and control branches in the software. However, the number of segments is also closely related to the change of the thrust-to-weight ratio, which is determined by the trajectory characteristics. Therefore, the moment when the CLG is introduced for the real-time control should be thoroughly studied.

Segmentation for continuous powered phases is applied in the LM-2F/Y8 mission. The CLG was introduced after the fairing was jettisoned. The second stage of the LM-2F was operating at that moment, which was equipped with five engines, i.e., one high-thrust main engine and four low-thrust swing engines. Thus, the flying was divided into two segments: all five engines were working, or only four swing engines were working after the main engine was shut down. During the working phase of the five engines, the equivalent impulse for the second flight segment is set based on the theoretical values of four swing engines; when the main engine shut down, it was updated based on the apparent acceleration measured by the IMU. Thus, the state equations were no longer continuous when facing different powered phases. An example including two powered phases (two burns) and a coasting phase in between is shown in Fig. 2.5.

Fig. 2.5

Thrust variation with a coasting phase

The time-to-go has three components:

$$\begin{aligned} {t_k} = {t_{k1}} + {t_{k2}} + {t_{k3}}. \end{aligned}$$

(2.62)

The corresponding apparent acceleration is as follows:

$$\begin{aligned} {\dot{W}_{x1}}(t) = \left\{ \begin{array}{l} \begin{array}{cc} {\frac{{I_{sp1}}}{{{\tau _\mathrm{{1}}} - t}}}&{}{{t_a} \le t< {t_b}} \end{array}\\ \begin{array}{cc} {0\begin{array}{cc} {}&{}{} \end{array}}&{}{{t_b} \le t < {t_c}} \end{array}\\ \begin{array}{cc} {\frac{{I_{sp3}}}{{{{\tilde{\tau }}_\mathrm{{3}}} - t}}}&{}{{t_c} \le t \le {t_d}} \end{array} \end{array} \right. . \end{aligned}$$

(2.63)

As discussed above, ${{\tilde{\tau }}_\mathrm{{3}}}$ is set as a theoretical value during the iterative computing of the first burn and then updated by the real flight data when the second burn initiates. Thus, the closed-loop guidance across different flight phases are implemented by replacing Eq. (2.28) with Eq. (2.63).

2.3.2.2 IGMs with Terminal Attitude Constraints

The guidance command is realized by adjusting the attitude of the launcher. To meet the terminal velocity and position constraints simultaneously at the orbit entry point, the guidance law requires the attitude to be tuned to a certain state to satisfy the thrust vector requirements. Furthermore, the actual flight path would deviate from the planned trajectory because of the existence of interferences and model uncertainties. These lead to large dispersions between the real and nominal attitude when the payload is released, and the degree of dispersions is mainly related to the magnitude of the interferences and the flight accelerations.

The missions with terminal attitude constraints are not uncommon, and usually a reaction control system (RCS) is configured to regulate the attitude after the orbit injection. However, if the guidance method could satisfy the constraints, the RCS could be omitted to simplify the launcher, improve the reliability, and reduce the cost. This demands that the guidance method satisfies OEs and attitude constraints simultaneously only through the thrust vector control of the pitch, yaw, and cutoff sequences.

An upgraded quadratic time-to-go function expressing the thrust direction is proposed to meet the terminal attitude constraints, i.e., Eq. (2.29) is modified as follows:

$$\begin{aligned} \left\{ \begin{array}{l} {\varphi _{cx}}\left( t \right) = \tilde{\varphi }+ \left( { - {k_1} + {k_2} \cdot t + {k_5} \cdot {t^2}} \right) \\ {\psi _{cx}}\left( t \right) = \tilde{\psi }+ \left( { - {k_3} + {k_4} \cdot t + {k_6} \cdot {t^2}} \right) \end{array} \right. . \end{aligned}$$

(2.64)

The two new variables, $k_5$ and $k_6$, can be obtained based on the terminal pitch and yaw attitude constraints. The solving of these new variables can be found in Ref. [15], and the method is applied in the LM-2F/ T3 mission.

However, the terminal attitude cannot be set arbitrarily in this way. If the angle between the thrust and the terminal velocity direction is too large, the assumption that $k_1$-$k_6$ are small does not hold. This is the premise for deriving an analytical guidance law by simplifying the trigonometric functions. In the next section, another prediction and correction algorithm is proposed and compared to tackle the same problem.

2.3.3 Prediction-Correction Iterative Guidance Method

To avoid the singularity in the solving of the IGM when approaching the cutoff moment, the iterative calculation is terminated in advance before the engine shuts down. The variables of the guidance law then remain unchanged for the follow-up control. The errors arising therefrom should be compensated for, which is the initial purpose of the prediction-correction IGM. Its process is described as follows [38]:

(1) Based on Eq. (2.29), calculate the pitch and yaw commands when the IGM is terminated, $\phi ({t_{f0}})$ and $\psi ({t_{f0}})$, respectively, where ${t_{f0}} = {t_f} - \Delta t$ , $t_f$ represents terminal time, and $t_{f0}$ is the moment when the IGM is terminated.

(2) Construct the apparent acceleration model $\dot{W}_{x1}(t)$:

$$\begin{aligned} {\dot{W}_{x1}}(t) = \frac{{{I_{sp}}}}{{\tau (t) - t}}, \end{aligned}$$

(2.65)

where $\tau (t) = m({t_{f0}})/\dot{m}(t)$, and t takes ${t_{f0}}$ as the starting point:

$$\begin{aligned} {\dot{W}_{x1}}({t_{f0}}) = \frac{{{I_{sp}}}}{{\tau (t) - 0}}. \end{aligned}$$

(2.66)

Then,

$$\begin{aligned} {\dot{W}_{x1}}(t) = \frac{{{I_{sp}}}}{{\frac{{{I_{sp}}}}{{{{\dot{W}}_{x1}}({t_{f0}})}} - t}}. \end{aligned}$$

(2.67)

(3) Calculate the increases in the apparent velocity (or velocity) and position from ${t_{f0}}$ to ${t_f}$, and then obtain the predicted terminal state $\mathbf{{X}}_k^*({t_f})$ under this condition, which can be expressed as a function of the following variables:

$$\begin{aligned} \mathbf{{X}}_k^*({t_f}) = f_\textrm{pts}({\mathbf{{X}}_k}({t_{f0}}),\phi ({t_{f0}}),\psi ({t_{f0}}),{\dot{W}_{x1}}(t)). \end{aligned}$$

(2.68)

where $f_\textrm{pts}$ denotes the function to calculate the terminal state.

The thrust vector remains the same after ${t_{f0}}$.

(4) Calculate the compensation to the terminal constraints $\Delta \mathbf{{X}}_k(t_f)$ as follows:

$$\begin{aligned} \Delta {\mathbf{{X}}_k}({t_f}) = {\mathbf{{X}}_k}({t_f})\mathrm{{ - }}{} \mathbf{{X}}_k^*({t_f}). \end{aligned}$$

(2.69)

(5) Update the terminal constraints $\mathbf{{X}}_k(t_f)$:

$$\begin{aligned} {\mathbf{{X}}_k}({t_f}) \leftarrow {\mathbf{{X}}_k}({t_f}) + \Delta {\mathbf{{X}}_k}({t_f}). \end{aligned}$$

(2.70)

The terminal constraints, which include the velocity and position constraints, were formerly determined by the entry point, however Eq. (2.70) renews them based on error predictions, while the time-to-go remains the same. Then, the variables of guidance law is re-calculated based on Eq. (2.70) in the current guidance cycle. Although these updated terminal constraints are not strictly optimal, the simulations show that the resulting errors are acceptable.

For different application scenarios, Eq. (2.69) has various updates. Note that $\Delta {\mathbf{{X}}_k}({t_f})$ represents the terminal constraint compensation induced by various factors during the period from ${t_{f0}}$ (or other moments we are interested in) to ${t_f}$. These compensations are due to the systematic errors caused by conditions such as the in-advance termination of the IGM, the deviations caused by the tracking control or the cutoff thrust, and the other processing such as the attitude regulation.

2.3.3.1 Direct Injection Under High Thrust

Under high-thrust conditions before a payload is released to an orbit, the same attitude tracking error would result in large lateral or normal velocity deviations, and the disturbances and the uncertainties of the cutoff thrust also increase. All the above effects are adverse to the entry accuracy, and this is what LM-7 faces when launching cargo spacecrafts.

In general, a terminal velocity correction system (TVCS) could be installed to reduce the velocity errors after the main engines were shut down, but this auxiliary system would increase the complexity and cost of the launcher, reduce the carrying capacity and reliability. The final solution of LM-7 is to shut down two fixed engines in the last stage ahead of the cutoff of two other swing engines to reduce the overload before entering into an orbit. The time interval between these two cutoffs should not be too long to affect the launcher’s performance, but a short interval would lead to a rapid time-varying thrust due to the coupling of the cutoff thrusts of four engines, and prominent variations in the guidance commands because the position constraints are very sensitive to the thrust. This leads to the increases in the attitude tracking errors and the injection deviations. To tackle this dilemma, the position constraints of the CLG are relaxed just before the cutoff of two fixed engines, letting the guidance commands quickly enter into a stable state. Although this strategy would produces systematic position errors, but a relatively accurate prediction of the terminal position is realized due to the stable guidance commands and high tracking accuracies, thus a prediction-correction scheme could be adopted before the shutdown of the two fixed engines.

The state vector at time ${t_f}$, $\mathbf{{X}}_k^{(2)}({t_f})$, which indicates the scenario that only two swing engines operate while the other two fixed engines shut down, could be predicted through the motion equation of the last stage in the vacuum regime. It should be pointed out that after two fixed engines shut down, ${t_f}$ would not be updated again.

Similarly, ${\mathbf{{X}}_k}({t_f})$ represents the state vector predicted by the CLG if the four engines shut down simultaneously in the end. The deviation is solved as follows:

$$\begin{aligned} \Delta \mathbf{{X}}_k^{}({t_f}) = \mathbf{{X}}_k^{}({t_f}) - \mathbf{{X}}_k^{(2)}({t_f}). \end{aligned}$$

(2.71)

The above deviation is introduced into the IGM terminal constraint:

$$\begin{aligned} \mathbf{{X}}_k^{}({t_f}) \leftarrow \mathbf{{X}}_k^{}({t_f}) + \Delta {\mathbf{{X}}_k}({t_f}). \end{aligned}$$

(2.72)

The control variables of the IGM would not update when the two fixed engines shut down and remain unchanged until the end of the flight. More detailed discussion can refer to Ref. [13].

2.3.3.2 Error Correction of Terminal Velocity

Even if the TVCS is configured, the process of velocity corrections is general open-loop. The entry accuracy mostly depends on whether the state vectors at the cutoff time are consistent with the theoretical conditions. Owing to the influences of various disturbances and deviations (such as thrust deviations), it is most probable that the terminal state differs from the expected value. Thus, the open-loop velocity correction based on the prescribed command sequences will lead to non-negligible velocity errors, which is disadvantageous to the orbit entry accuracy. This problem can also be solved by the prediction-correction strategy, but at this time, only the terminal velocity would be corrected.

After the engines shut down, the velocity increments caused by the cutoff thrust can be predicted as follows in the target OCS:

$$\begin{aligned} \left\{ \begin{array}{l} \Delta {W_{xcf}} = \int _{{t_f}}^{{t_{cut}}} {{{\dot{W}}_{cf}}(t)\cos \phi _f^*\cos \psi _f^*dt} \\ \Delta {W_{ycf}} = \int _{{t_f}}^{{t_{cut}}} {{{\dot{W}}_{cf}}(t)\sin \phi _f^*\cos \psi _f^*dt} \\ \Delta {W_{zcf}} = \int _{{t_f}}^{{t_{cut}}} {{{\dot{W}}_{cf}}(t)\sin \psi _f^*dt} \end{array} \right. . \end{aligned}$$

(2.73)

where $\varphi _f^*$, $\psi _f^*$ are the real pitch and yaw control commands at the cutoff moment, ${\dot{W}}_{cf}$ is the apparent acceleration of the cutoff thrust, $t_{cut}$ is the moment when the cutoff thrust ends, $\Delta {W_{xcf}}$, $\Delta {W_{ycf}}$, $\Delta {W_{zcf}}$ are the apparent velocity increments induced by the cutoff thrust under $\varphi _f^*$, $\psi _f^*$ commands.

Similarly, the nominal apparent velocity increments based on the prescribed pitch and yaw angles can also be obtained as ${[\Delta {W_{xf}},\Delta {W_{yf}},\Delta {W_{zf}}]^T}$, and then,

$$\begin{aligned} \Delta {\mathbf{{X}}_k}({t_f}) = {[\Delta {W_{xf}} - \Delta {W_{xcf}},\Delta {W_{yf}} - \Delta {W_{ycf}},\Delta {W_{zf}} - \Delta {W_{zcf}},0,0,0]^T}. \end{aligned}$$

(2.74)

This scheme plays a major role in the LM-8/Y1 mission. The deviation between the terminal pitch command of the IGM and the nominal condition was $10.5^\circ$, and if no measures were adopted, the velocity errors caused by cutoff thrust would exceed the TVCS’s correction ability, resulting in a timed shutdown of the TVCS (its working time was scheduled as 40 s). Thus, the velocity errors would not be fully compensated for, thereby affecting the injection accuracy. Benefiting from the above algorithm, the timed shutdown of the TVCS was avoided, and the accuracy of the semi-major axis was ensured and greatly improved.

2.3.3.3 Handling of Terminal Attitude Constraints

Based on the prediction-correction strategy, a new approach different from that in Sect. 2.3.2.2 is discussed to handle terminal attitude constraints. IGM is terminated at time ${t_{f0}}$, which is close to the terminal time $t_f$, and then an attitude adjustment phase is introduced to regulate the thrust vector from the current values $\phi ({t_{f0}})$, $\psi ({t_{f0}})$ to the expected terminal states ${\phi _f}$, ${\psi _f}$. Taking the pitch channel as an example, the expression of the attitude adjustment is as follows:

$$\begin{aligned} \phi (t) = \left\{ \begin{array}{l} \frac{{2({\phi _f} - \phi ({t_{f0}}))}}{{{{({t_{f1}} - {t_{f0}})}^2}}}{(t - {t_{f0}})^2} + {\phi _{f0}},{t_{f0}} \le t \le \frac{{{t_{f1}} + {t_{f0}}}}{2}\\ - \frac{{2({\phi _f} - \phi ({t_{f0}}))}}{{{{({t_{f1}} - {t_{f0}})}^2}}}{(t - {t_{f1}})^2} + {\phi _f},\frac{{{t_{f1}} + {t_{f0}}}}{2}< t \le {t_{f1}}\\ {\phi _f},{t_{f1}} < t \le {t_f} \end{array} \right. , \end{aligned}$$

(2.75)

where $t_{f1}$ is the moment when the attitude adjustment ends, $\phi \left( t \right)$ represents the thrust vector at time t, and the expression $\psi \left( t \right)$ in the yaw channel is similar and not repeated.

The apparent acceleration during the attitude adjustment can be expressed as

$$\begin{aligned} {\dot{W}_{x1}}(t) = \frac{{{I_{sp}}}}{{\tau - t}}. \end{aligned}$$

(2.76)

Based on Eqs. (2.75) and (2.76), we can determine the terminal state as follows:

$$\begin{aligned} {\mathbf{{X}}_k^*({t_f}) = f_\textrm{pts}({\mathbf{{X}}_k}({t_0}),\phi (t),\psi (t),{{\dot{W}}_{x1}}(t))} . \end{aligned}$$

(2.77)

The terminal compensation is

$$\begin{aligned} \Delta {\mathbf{{X}}_k}(t{}_f) = {\mathbf{{X}}_k}(t{}_f) - \mathbf{{X}}_k^*(t{}_f). \end{aligned}$$

(2.78)

Three cases under different methods, i.e., the fundamental CLG (labeled as Case1_0), the method introduced in this section (labeled as Case1_1), and the method introduced in Sect. 2.3.2.2 (labeled as Case1_2), are compared in the Fig. 2.6, where ${F_{CX}}$ and ${P_{CX}}$ represent the pitch and yaw Euler angles, respectively.

Fig. 2.6

Comparisons of Euler angles

Compared with the method introduced in Sect. 2.3.2.2, we can see an obvious attitude regulation process before entering into an orbit, and the guidance commands before the adjustment are more consistent with that of the fundamental method.

2.4 Joint Optimization of Target Orbit and Flight Path

For most launch failures caused by a thrust drop, the engines can continue to operate without an explosion. If the engines deteriorate to a very risky level indicated by the sensed data, active shutdown is preferable to ensure flight safety. No matter what measures are taken, the carrying capacity will degrade. If still using the prescribed guidance law under this situation, whether an orbit is reachable depends on the remaining carrying capacity. Under severe failures, the propellant will be exhausted inflight, the terminal velocity and position will not be able meet the requirements of circling the Earth, and LV/payloads will crash to the ground. Thus, onboard decision making is required in the above situations to save missions.

The assumption for analytical CLGs is that we can always find an injection point on the PTO that matches the current flight states, and how to find the target orbit is not within the scope of guidance methods. However, this assumption does not hold if the PTO is beyond the performance capabilities of the rocket. A possible rescue orbit in which the rocket makes use of the remaining fuel should be found first, then the flight path should be planned or solved concurrently. A rescue orbit refers to a new target that is different from the PTO, where the payloads can enter as the starting point for the follow-up orbital transfer to avoid crashing. It has the same meaning as a parking orbit in most contexts, where the satellite can circle the Earth for many rounds. To consume as little fuel as possible by the payloads during the orbit transfer, an optimal rescue orbit becomes attractive. Under special conditions, a rescue orbit can also be a sub-orbit with a negative perigee height. The payload could not circle the Earth under this condition and should initiate the orbit transfer as soon as possible when released by the rocket.

It is difficult to find an analytical optimal rescue orbit, so a numerical method is usually adopted. This problem was first discussed in Refs. [40, 41]. In Ref. [40], the errors of different OEs were regulated through weights of element deviations in the objective. In Ref. [41], sequential optimization was conducted based on state-triggered-indices (STI), so as to gradually approach the optimal rescue solution. A convex optimization (COP) sub-problem was constructed, and its solution was taken as the initial value of the rescue planning problem. During the COP process, the geocentric angle of the injection point after the failure is estimated referring to the IGM process, then the COP sub-problem is transformed to the OCS to simplify the terminal constraints. This treatment greatly improves the calculation efficiency of the COP. Reference [39] proposed solutions for the maximum orbital radius optimization if the rescue orbit were confined to a circular orbit. However, none of the above methods can adapt to the flight scenario where a coasting phase is inserted. In Ref. [43], an autonomous mission reconfiguration algorithm considering the coasting phase was discussed to handle the typical failure modes that occur in real launchers, but the coasting orbit and the command sequences during coasting still refer to the prescribed planning results. This treatment can obtain a feasible solution when failures occur, but it may not make full use of the remaining performance. Thus the study of the multiple graded optimization (MGO) continues, while solving the MGO online is still very challenging.

2.4.1 State-Triggered-Indices (STI) Based Method for Continuous Powered Phases

The process of the STI-based optimization is explained in Fig. 2.7 [41]. The impacts of the deviations of the OEs on the fuel consumed to correct these errors are closely related to the orbital characteristics and the launcher’s current state, which exhibit strong nonlinear features. Thus, the objective in Fig. 2.7 cannot be solved directly because of the concerns on the convergence or local optimal solutions, and it is transferred to three sub-problems.

Fig. 2.7

Framework of STI method

(1) For the sake of safety, the orbital height should be ensured first after a failure occurs, so the first reaction is to find a maximum height circular orbit (MCO).

If the height is less than a safety value, it means the rocket can hardly stay in any orbit, the rescue is then abandoned. If the height meets the safe threshold but is less than the perigee height of the PTO, the circular orbit is then taken as the rescue orbit (optimal circular orbit, OCO). However, if the height is much higher, it indicates that there is a certain performance margin used to adjust other OE errors. Then, the next planning is triggered.

(2) The orbital inclination and LAN are regulated while ensuring the height of the perigee to obtain the optimal eclipse orbit (OEO).

The deviations of the inclination and LAN are eliminated as much as possible while keeping the perigee height of the rescue orbit around the required value. If the rescue orbit can be coplanar with the PTO, the following planning will be triggered again.

(3) The argument of the perigee, semi-major axis, and eccentricity are regulated while maintaining the perigee height and orbital planar elements to obtain the optimal rescue orbit (ORO).

During the optimization, the solution of the current sub-problem is taken as the initial guess of the next sub-problem. The initial guess can meet the equality constraints of all the motion equations, improving the convergence and efficiency of the numerical computation. However, to obtain a reasonable initial guess value of the first sub-problem, the nonlinear terminal constraints of the OEs are transformed to the OCS. This idea is inherited from the IGM, and the transformation matrix is as follows:

$$\begin{aligned} {G_O} = \left[ {\begin{array}{*{20}{c}} { - \sin {\Omega _0}\cos {i_0}}&{}{\cos {\Omega _0}\cos {i_0}}&{}{\sin {i_0}}\\ {\cos {\Omega _0}}&{}{\sin {\Omega _0}}&{}0\\ { - \sin {\Omega _0}\sin {i_0}}&{}{\cos \Omega \sin {i_0}}&{}{ - \cos {i_0}} \end{array}} \right] \left[ {\begin{array}{*{20}{c}} {\cos {\Phi _k}}&{}{ - \sin {\Phi _k}}&{}0\\ {\sin {\Phi _k}}&{}{\cos {\Phi _k}}&{}0\\ 0&{}0&{}1 \end{array}} \right] , \end{aligned}$$

(2.79)

where $\Phi _k$ is the geocentric angle between the orbit entry point and the ascending node (see Fig. 2.3).

In the OCS labeled as $O-\xi \eta \zeta$, the position components along the $O\xi$ and $O\zeta$ axes are 0, and the velocity components along the $O\eta$ and $O\zeta$ axes are 0. The terminal constraints are summarized as follows:

$$\begin{aligned} \begin{array}{*{20}{c}} {{\xi _f} = {\zeta _f} = 0,}&{{V_\eta } = {V_\zeta } = 0,}&{\mu = {\eta _f}V_{\xi f}^2.} \end{array} \end{aligned}$$

(2.80)

Compared with the constraints in the LICS, i.e., Eqs. (2.16)–(2.23), (2.80) is greatly simplified, where ${\Phi _k}$ in Fig. 2.3 can be predicted as follows [40]:

$$\begin{aligned} {\Phi _k} = {\Phi _0} + d\Phi , \end{aligned}$$

(2.81)

where $\Phi _0$ is the geocentric angle between the position of the launch vehicle at the current time and the ascending node, and $d\Phi$ is the geocentric angle in the current orbital plane during the remaining flight range.

$$\begin{aligned} d\Phi \approx \frac{{d{\Phi _{ref}}}}{\kappa }, \end{aligned}$$

(2.82)

where $\kappa$ is the percentage of nominal thrust after a failure occurs.

$$\begin{aligned} d{\Phi _{ref}} = \arccos \left( {\frac{{{\mathbf{{P}}_{ref}} \cdot {\mathbf{{P}}_0}}}{{\left\| {{\mathbf{{P}}_{ref}}} \right\| \cdot \left\| {{\mathbf{{P}}_0}} \right\| }}} \right) . \end{aligned}$$

(2.83)

An example is given below. For a PTO with ${h_{\!p}} =$ 200 km and ${h_{a}} =$ 300 km, the corresponding OEs are shown in Table 2.1. It is assumed that the thrust reduction is caused by the decrease in the mass flow rate at 118.2 s, and the remaining thrust is 77.94%. The results in Fig. 2.8 were obtained by the STI-based processing.

Table 2.1 Orbital elements of prescribed target orbit

Fig. 2.8

Trajectories of rescue results

$\mathrm Traj_{ref}$ is the nominal flight path. At the fault moment, $\Phi _k$ is estimated as $171.05^\circ$, and $d{\Phi _{est}} = 15.6475^\circ$. The OCS can be established when ${i_0} = 41.27^\circ$ and ${\Omega _0} = 315.51^\circ$ at the fault time. The result of the COP is shown by the blue line labeled $\mathrm Traj_{CVX}$, which can be taken as the initial guess for the OCO by the adaptive collocation method. The OCO result is represented by $\mathrm Traj_{OCO}$, and $d{\Phi _{act}} = 15.6496^\circ$, showing that the deviation from the estimated value is $0.0021^\circ$.

Since the height of OCO is 208.8 km, which is greater than the $h_p$ of the PTO, then the following planning is triggered, where $[{\lambda _{hp}},{\lambda _a},{\lambda _i},{\lambda _\Omega }] = [10^{-3}, 10^{-3}, 1, 1]$. The result is shown as $\mathrm Traj_{OEO}$ with ${h_{\!p}} =$ 200.1 km and ${h_a} =$ 215.6 km.

By defining ${\varepsilon _i} = {\varepsilon _\Omega } = 0.05^\circ$, $\Delta i$ and $\Delta \Omega$ are both less than $0.05^\circ$, triggering the next planning. The result of the ORO is represented as $\mathrm Traj_{ORO}$, and the OEs are summarized in Table 2.2.

Table 2.2 Orbital elements of OCO, OEO and ORO

Because the first planning of the OCO needs to solve the COP problem to obtain the initial guess, the calculation time accounts for more than 60% of the total planning time. By taking the OCO as the initial value, the solutions of the OEO and ORO problems can converge quickly.

More detailed discussion can be found in Ref. [41].

2.4.2 Segmented Rescue Optimization Crossing Coasting Phase

If a coasting phase is inserted into the optimization of the rescue orbit, the complexity of on-line planning will be further increased. Thus, a segmented planning strategy (SPS) is studied first, and the continuous solution is discussed in the next section. The SPS is similar to the IGM across the coasting phase, i.e., the coasting obit is taken as the target orbit of the first burn. Under nominal conditions, the IGM across the coasting arc does not lose optimality, because the terminal constraints of each flight phase are reachable. However, these constraints might not best match the remaining performance and guidance command sequences when a failure occurs, leading to the handover conditions between phases being unreachable.

However, the SPS relaxes the computational burden of online planning and demonstrates its effectiveness under the typical failure modes [42]. Under the background of launching satellites to the GTO using a two-stage rocket, its solutions are briefly explained as follows:

(1) Identify the fault mode first.

Three failure modes are considered. If the engine is going to explode, shut it down immediately, and let the subsequent stages make up for the performance loss of the premature cutoff. If an engine fails to start or shuts down by accident, restart it again if it has multiple burns. The restart may succeed or fail; even if it succeeds, it will make the engine unable to operate the following scheduled startup owing to the restriction on re-ignition times. However, the restarting scheme has the effect of postponing the fault moment and reducing the impact on the performance degradation. If only the thrust drops and there is no emergent risk, let the engine continue working. In the discussion in this section, it is assumed that there is no leakage, and all the remaining propellants can be utilized.

(2) Judge the flying regimes. If flying in the atmosphere and considering the landing area of the rocket debris, call the PGM for the tracing control until the fuel in the boosters is exhausted, then turn off the engines.

(3) If flying out of the atmosphere, evaluate the remaining performance by the ES-IGM algorithm [42].

If flying before coasting, first evaluate whether the prescribed coasting orbit is reachable; if flying after coasting, evaluate whether the PTO is reachable. The ES-IGM algorithm is based on the numerical integration and summarized in Ref. [42].

(4) Call the STI to optimize the new orbit and flight path if the prescribed orbit is beyond the remaining performance capabilities; otherwise, call the IGM for the guidance control.

The above algorithm is an approximate processing because the coasting phase is not optimized according to the fault state. If the coasting orbit is still reachable, the guidance command consequence is inherited during the coasting; if not, a new transfer orbit is planned by the STI method, and the triggering of the second burn is scheduled nearby the apogee of the new coasting orbit.

The discussion in Ref. [42] indicated that, if the PGM is adopted from the current point to the end or if the IGM is called only during the last burn, the LV/satellite may fall out of space under fault conditions with a high probability. In contrast, if the IGM is called as early as possible, the payload could be deployed into an orbit. This echoes the previous conclusions, the earlier the IGM is adopted inflight, the stronger the fault adaptability becomes. However, the IGM cannot guarantee a safe parking orbit, so the evaluation of the remaining performance is very important to support onboard decision making.

2.4.3 Multiple Graded Optimization

The STI method specifies the minimum orbital height as a safety constraint, for example, not less than 150 km. Thus, the satellite could circle the Earth and then carry out an orbital transfer at an appropriate point. If taking the payload as the final stage of a launcher, the flight process of the LV/payload can be jointly optimized, which is the meaning of the E2E optimization. At this time, we can relax the safety restrictions on the orbital height, even plan a sub-orbit (the perigee height is negative) to increase the apogee height, and make the orbital transfer responsively when flying to the apogee. E2E optimization can reduce the propellant consumed during the orbital transfer.

With the increase in commercial launches and constellations, multiple-satellite ridesharing launches are becoming more and more common. The purpose of the MGO is to separate some payloads in advance during the coasting phase while sending the remaining payloads to the PTO if the performance of the launcher is greatly reduced.

To clearly explain the MGO problem, the trajectory planning problems of the powered-coasting-powered profiles are summarized in Table 2.3. Offline numerical optimization is applied to analyze and compare the features of IGM, autonomous coasting reconstruction (ACRC), and MGO under thrust drop failures.

Table 2.3 Description of typical optimization problems

In Table 2.3, $\boldsymbol{F}_T$ is the nominal thrust, $F^1_T$ and $F^2_T$ are the nominal thrust magnitude of the 1st and the 2nd powered phase, respectively, and $\kappa$ is the percentage of the remaining thrust to its nominal value; $t_0$ and $t_f$ are defined as the fault time and the terminal time of the second stage, $t_1$ and $t_2$ are the engine cutoff time of the 1st powered phase and the start time of the 2nd powered phase, respectively; $t_{c0}$, $t_{cf}$ are the initial and terminal times of the coasting phase; $t_{1\max }$ and $t_{cool}$ are the maximum first burn time and the engine cooling time; $t_{c\max }$, $t_{2\min }$ are the maximum coast phase time and the minimum second burn time; $t_{coast}$ is the standard coasting time, $m_{\min }$ and $m_{sep}$ are the minimum mass of the rocket and the separation mass off the payloads.

For the IGM, the coasting OEs $\left[ {{a_c},{e_c},{i_c},{\Omega _c},{w_c}} \right] = Fun\left( {\boldsymbol{r}\left( {{t_1}} \right) ,\boldsymbol{V}\left( {{t_1}} \right) } \right)$ are introduced as the terminal constraints in the first powered flight phase. After entering the coasting phase, a timed schedule is applied as the startup condition of the second powered flight phase. Then, the IGM is called again to fly to the PTO.

For the ACRC method, the planning of the powered-coasting-powered profiles is optimized simultaneously while taking all payloads as a whole, so the coasting orbit will be re-planned, and there are no fixed OEs as the constraints of the first burn. The coasting time is planned onboard only considering the cryogenic propellant management and the precooling time required to restart engines. The terminal mass constraint is the same as that of the IGM.

Compared with the ACRC, the MGO method considers the solution of departing parts of the payloads during the coasting. Thus, $m\left( {{t_{c0}}} \right) = m\left( {{t_1}} \right) - {m_{sep}}$, and the terminal mass constraint of the second burn is reduced accordingly.

• Fault adaptability analysis

The following analysis is based on a two-stage launcher, and the launch site and PTO parameters are shown in Tables 2.4 and 2.5.

Table 2.4 Main parameters

Table 2.5 Parameters of PTO and launch site

We set ${t_{cool}}$ as 60 s, ${t_{c\max }}$ as 850 s, and $t{}_{2\min }$ as 50 s. The adaptive collocation method is used to plan the nominal trajectory of the launcher off-line, as shown in Fig. 2.9. The superscript ‘1st’ represents the flight state during the flight phase when the side and core boosters are working, and ‘2nd’, ‘3rd’, and ‘4th’ represent the first burn, coasting, and second burn of the second stage, respectively. According to the optimization results, the performance of the rocket is 5840 kg without considering the orbital height constraints of the coasting orbit.

Fig. 2.9

Parameters of the nominal flight trajectory

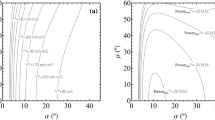
According to the nominal trajectory, ${t_{coast}}$ in the IGM is defined as 528.5 s. It is assumed that the launcher carries 10 identical satellites, each weighing 584 kg. The failure time is introduced in the time interval of 200–350 s of the first burn, and the thrust after failure occurs is represented by a factor $\kappa$. The simulation results are shown in Fig. 2.10, where S3 represents the fault adaptation range of the IGM, S2 represents the range of the ACRC, which is more than that of the IGM, and S1 represents the range of the MGO, which is greater than that of the ACRC. Method 1 and Method 2 represent the lower limits of fault adaptation ranges of the IGM and ACRC, respectively, and Method 3-1 and Method 3-2 represent the lower limits of the MGO corresponding to departing 5 or 9 satellites during coasting, respectively.

Fig. 2.10

Fault adaptation ranges

For Method 1, the IGM can only endure the thrust dropping by 10% if the failure occurs at 200 s. With the delay of the failure, the dropping tolerance increases exponentially, and 33% of the total thrust can still send the payloads to the PTO if the failure occurs at 350 s. For Method 2, if the coasting could be re-planned online, the allowable dropping thrust could be extended to 64% at 200 s and 6% at 350 s. If the failure state of the thrust were deteriorated beyond the lower limit, for example, thrust dropping to 45% at 200 s, all the payloads could not enter into the PTO. However, for Method 3-1 under this condition, the MGO could send half of the payloads to the PTO by releasing the other half during coasting, avoiding the complete loss of the mission. The more payloads released during the coasting, the more severe thrust drop failure could be endured, but fewer payloads would be sent to the PTO.

Compared with the IGM, the ACRC could adaptively adjust the coasting orbital inclination and LAN by extending the flight time of the first burn, regulate the shape of the coasting orbit, and elevate its perigee height to reduce the fuel consumption of the second burn. For the MGO method, the main mission of the second burn was to elevate the apogee height by boosting the speed, so the acceleration of the second burn could be improved by releasing parts of the payloads in advance.

• Case analysis

A test case is provided shown in Table 2.6.

Table 2.6 Failure state of test case

If the minimum departure mass of 2625.5 kg could be determined onboard, five payloads should be separated in advance. With ${m_{sep}}$ as $5\times 584$ kg in the MGO, the optimization results are shown in Fig. 2.11.

Fig. 2.11

MGO planning results

The flight time of each phase by the MGO is shown in Table 2.7. The coasting OEs are shown in Table 2.8.

Table 2.7 Flight time

Table 2.8 Coasting orbital elements

In the above analysis, the coasting orbit is optimized as a sub-orbit, and the satellites released during the coasting will inevitably crash to the ground. Another solution is to constrain a minimum safe perigee height of the coasting orbit, so the departed satellites could still circle the Earth and wait for rescue, but the number of satellites that could be put into the PTO would greatly decrease. No matter which solution was adopted, the MGO could avoid the complete loss of payloads for rideshare launches.

However, the discussion in this section is based on off-line plannings, and onboard ACRC or MGO plannings are still challenging. A special issue is analyzed in Ref. [43], where the payload could still enter into the PTO by adjusting the coasting orbit.

2.5 Conclusions

Ascent guidance methods are a basic, fully studied, and seemly mature technology. The off-line planning and on-line tracking strategy were widely applied in the early stage and have achieved good results; they are even still used currently. Considering the wind load relief and the restrictions of the debris landing area, the OLG or tracking guidance is still playing a major role in endo-atmospheric flight.

CLGs perform well for exo-atmospheric guidance. No structural load constraints and atmospheric disturbances are considered. The optimization problem is then simplified to obtain analytical solutions based on optimal control theories. Compared with the tracking guidance, the CLGs are more adaptive to model uncertainties and interferences, and they are capable of satisfying multiple terminal constraints such as six OEs to obtain higher injection accuracies. If mild thrust drop failures occur, they can also be taken as disturbances handled by the CLGs.

It’s assumed that model uncertainties and disturbances are bounded. If the faults’ effect is far beyond the limits, the CLGs no longer work. Thus, the AGMs are attracting more interest. AGMs cannot ensure an entry into the PTO, because they cannot violate physical laws under severe failures, but they may reconstruct the mission to avoid the complete loss of the payloads.

In conclusion, the AGMs need to solve the following sub-problems: (1) onboard model identification or reconstruction, which mainly occurs in the case of abnormal conditions, such as loss of thrust; (2) evaluation of the remaining performance, which is to simplify the decision making: whether to use the CLGs to the PTO or to reconstruct the mission; and (3) determination of the optimization objectives, i.e., keeping the payload in an orbit, the end-to-end planning, or the graded optimization for rideshare launches.

Although there is no perfect or groundbreaking method to solve all the above problems, the collocation method with smart initial guesses provides a strategy for complex onboard planning. The convergence is not guaranteed, but it is better than doing nothing to let the LV/payload assembly fall from space. Any solution, although not optimal, is acceptable under these failure scenarios. The study of the AGMs to reconstruct the mission is just beginning, while the study of the analytical guidance is still important because it is often the first choice of the initial guess.