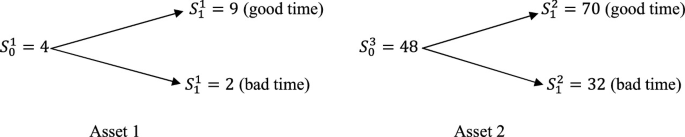Abstract
This chapter discusses how forward and futures contracts and options are related to corporate finance.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
E.g., Fama and Jensen (1983, p. 328) argue that “the residual risk—the risk of the difference between stochastic inflows of resources and promised payments to agents—is borne by those who contract for the rights to net cash flows. We call these agents the residual claimants or residual risk bearers”.
- 2.
See also the Robin Hood story in Chap. 2.
- 3.
This is an example of ‘expectation matters’, i.e., our expectations for the future will determine our current behavior.
- 4.
Strictly speaking, the Modigliani–Miller first proposition is: In a complete market with no transaction costs and no arbitrage, the market value of the firm is independent of its capital structure.
- 5.
The literature of derivatives (e.g., Hull (2018, p. 269) and Merton (1973b, p. 183)) incorrectly states the upper and lower bounds of the put options as: \(\frac{K}{1+r}\ge p\ge Max\left[\frac{K}{1+r}-{S}_{0}, 0\right]\) and \(K\ge P\ge Max\left[K-{S}_{0}, 0\right]\). Hull (2018, p. 270) and Merton (1973b, p. 183) erroneously argue that “the maximum pay-off to a European put is the exercise price, \(K\), which occurs if the underlying asset price \({S}_{0}\) is zero”. This argument is wrong because \({S}_{0}=0\) if and only if people believe \({S}_{t}=0, \forall t>0\). Since \({S}_{t}=0, \forall t>0\), is not a random variable, all options do not exist.
- 6.
The Gordan theory is a corollary of Farkas theory:
Let \(\boldsymbol{A}\) be a \(m \times n\) matrix and \(\boldsymbol{c}\in {R}^{n}\) be a vector. Then, exactly one of the following systems has a solution:
System 1: \(\boldsymbol{A}\boldsymbol{x}\ge 0\) and \({\boldsymbol{c}}^{t}\boldsymbol{x}<0\) for some \(\boldsymbol{x}\in {R}^{n};\)
System 2: \({\boldsymbol{A}}^{t}\boldsymbol{y}=\boldsymbol{c}\) and \(\boldsymbol{y}\ge 0\) for some \(\boldsymbol{y}\in {R}^{m}\).
The Farkas theory is a corollary of Separating Hyperplane Theory:
Let S be a nonempty, closed convex set in \({R}^{n}\) and \(\boldsymbol{y}\notin S\). Then, there exists a nonzero vector \(\boldsymbol{z}\in {R}^{n}\) and a scalar \(\alpha\) such that \({\boldsymbol{z}}^{t}\boldsymbol{y}<\alpha\) and \({\boldsymbol{z}}^{t}\boldsymbol{x}\ge \alpha\) for each \(\boldsymbol{x}\in S\).
- 7.
\({{\varvec{A}}}^{t}{\varvec{p}}=0\) And \({\varvec{p}}\) is a non-zero vector imply the rank of \({{\varvec{A}}}^{t}\), \(R({{\varvec{A}}}^{t})\), is less than \(m\). Unique solution for (\({p}_{1},...,{p}_{m}\)) and \({\sum }_{i=1}^{m}{p}_{i}=1\) imply \(R({{\varvec{A}}}^{t})=m-1\).
- 8.
Chang (2017) has shown that because an asset’s current price (e.g., \({S}_{0}=\$\mathrm{8,000}\)) is determined by people’s expectation of the asset’s future possible payoffs and their probabilities, the probabilities of the Gordan theory derived from \({S}_{0}\) (\(\mathrm{e}.\mathrm{g}., \pi \mathrm{ and }1-\pi\) in Eq. (9.15)) are the actual world (not the risk-neutral world) probabilities.
- 9.
The Black–Scholes-Merton option pricing model is:\(c = S_{0} \cdot N\left( {d_{1} } \right) - K \cdot e^{ - rT} \cdot N\left( {d_{2} } \right)\); \(p = Ke^{ - rT} \cdot \left[ {1 - N\left( {d_{2} } \right)} \right] - S_{0} \left[ {1 - N\left( {d_{1} } \right)} \right]\),
where \({d}_{1}=\frac{\mathit{ln}(\frac{{S}_{0}}{K})+(r+\frac{{\sigma }^{2}}{2})T}{\sigma \sqrt{T}}\), \({d}_{2}={d}_{1}-\sigma \sqrt{T}\).
- 10.
The Dupire formula.
- 11.
Chang (2015, pp. 49-51) has shown that when both u and d change, and let (\({S}_{0}u-{S}_{0}d\)) be the range, the sign of \(\frac{\partial c}{\partial ({S}_{0}u-{S}_{0}d)}=\frac{\partial p}{\partial ({S}_{0}u-{S}_{0}d)}\) could be positive or negative. The Black-Scholes-Merton option pricing model, on the other hand, has: \(\frac{\partial c}{\partial \sigma }=\frac{\partial p}{\partial \sigma }>0\), where \(\sigma\) is the volatility. Ross (1993, p. 470) and Chang (2014) have shown that with complete market, no transaction costs and no arbitrage, the Black-Scholes-Merton option pricing model has the restriction: \(r=\mu +\frac{1}{2}{\sigma }^{2}\).
- 12.
Under certainty, the example which uses Eq. (2.4) in Chapter 2 also shows the same result: \({r}_{S}={r}_{WACC}={r}_{B}\).
- 13.
In the Black–Scholes-Merton option pricing model, the p-index is:
\(\frac{p}{K} = \frac{p}{{e^{\delta T} S_{0} }} = e^{ - rT} \cdot \left[ {1 - N\left( {d_{2} } \right)} \right] - e^{ - \delta T} \cdot \left[ {1 - N\left( {d_{1} } \right)} \right]\), where \(d_{1} = \frac{{\ln \left( {e^{ - \delta T} } \right) + \left( {r + \frac{{\sigma^{2} }}{2}} \right)T}}{\sigma \sqrt T }\) and \(d_{2} = d_{1} - \sigma \sqrt T\).
Because \(\frac{\partial c}{\partial \sigma }=\frac{\partial p}{\partial \sigma }>0\), higher \(\sigma\) means higher risk of the asset’s providing at least \(\delta\) rate of return.
- 14.
This is financial diversification irrelevancy, i.e., it does not add or decrease value.
- 15.
Also, let the maximum value of the debt at \(t=T\) be: \(K={S}_{0}^{D}\left(1+{r}_{D}^{max}\right)\) where \({S}_{0}^{D}\) is the market value of the debt at \(t=0\). Then the debt’s call option is: \(c=0\) and the debt’s put-call parity is: \(0=\frac{0}{{S}_{0}^{D}(1+{r}_{D}^{max})}=\left[\frac{1}{1+{r}_{D}^{max}}-\frac{1}{1+r}\right]+\frac{p}{K}\).
- 16.
See also Proposition 9.2.
- 17.
Ross, Stephen (1998) The Mathematics of finance: pricing derivatives. Quarterly of Applied Mathematics 56: 695-706. Wilmott, Paul (2007) Paul Wilmott Introduces Quantitative Finance. John Wiley & Sons, West Sussex, England.
References
Black, F., & Scholes, M. (1973). The pricing of options and corporate liabilities. Journal of Political Economy, 81, 637–654.
Chang, K.-P. (2014). Some misconceptions in derivative pricing. http://ssrn.com/abstract=2138357.
Chang, K.-P. (2015). The ownership of the firm, corporate finance, and derivatives: Some critical thinking. Springer Nature.
Chang, K.-P. (2016). The Modigliani-Miller second proposition is dead; long live the second proposition. Ekonomicko-manažerské Spektrum, 10, 24–31. http://ssrn.com/abstract=2762158.
Chang, K.-P. (2017). On using risk-neutral probabilities to price assets. http://ssrn.com/abstract=3114126
Chang, K.-P. (2023). Measuring risk structures of assets: p-index and c-index. http://ssrn.com/abstract=4352457
Chang, K.-P. (2020). On option Greeks and corporate finance. Journal of Advanced Studies in Finance, 11, 183–193. https://doi.org/10.14505/jasf.v11.2(22).09
Cox, J., Ross, S., & Rubinstein, M. (1979). Option pricing: A simplified approach. Journal of Financial Economics, 7, 229–263.
Fama, Eugene and Michael Jensen. (1983). Agency problems and residual claims. Journal of Law and Economics, 26, 327–349.
Hull, J. (2018). Options, futures, and other derivatives. Pearson Education Limited.
Merton, R. (1973a). Theory of rational option pricing. Bell Journal of Economics and Management Science, 4, 141–183.
Merton, R. (1973b). The relationship between put and call option prices: Comment. Journal of Finance, 28, 183–184.
Myers, S. (1984). The search for optimal capital structure. Midland Corporate Finance Journal, 1, 6-16; also in Stern, J. M., & Chew, D.H., Jr. (Eds.). (1986). The revolution in corporate finance (pp. 91-99). Basil Blackwell
Stoll, H. (1969). The relationship between put and call option prices. Journal of Finance, 24, 801–824.
Author information
Authors and Affiliations
Corresponding author
Appendix: Do Arbitrage When System 2 of the Gordan Theorem Fails
Appendix: Do Arbitrage When System 2 of the Gordan Theorem Fails
Assume a one-period, two states (good time and bad time) of nature world with no transaction costs (i.e., a perfect market). There are two assets: a money market (Security 1) which provides \(1+0.25\) dollars at \(t=1\) if one dollar is invested at \(t=0\) (i.e., the risk-free interest rate is \(r=0.25\)), and two other securities (Security 2 and Security 3) with current market prices $4 and $48, respectively, which at \(t=1\) provide:

That is, at \(t=1\), when Security 2 provides $8, Security 3 will provide $70; and when Security 2 provides $2, Security 3 will provide $30. In this case, the two securities are not governed by the same probability measure (i.e., System 2 of the Gordan (Arbitrage) Theorem has no solution):
i.e., we cannot find a vector \({\varvec{p}}=\left[\begin{array}{c}\pi \\ 1-\pi \end{array}\right]\), \(0\le \pi \le 1\), such that System 2 holds:
By System 1 of the Arbitrage Theorem, there must exist an arbitrage opportunity. For example, at\(t=0\), we can short sell one share of Security 3 and buy 5 shares of Security 2 and invest $28 \((=48-4\times 5)\) in the money market, and at \(t=1\) we can earn excess profits, i.e.,
When investors adopt this arbitrage strategy at \(t=0\), the market price of Security 2 will go up and that of Security 3 will go down. In equilibrium (i.e., no arbitrage), the market prices of the two securities at \(t=0\) will adjust to the point that they all are priced by the same probability measure, say, \({\varvec{p}}=\left[\begin{array}{c}2/3\\ 1/3\end{array}\right]\),
or
Since, in the above equation, the rank of the matrix \({\varvec{A}}\) is: \(1 = m - 1\), the market is complete, and the probability measure \({\varvec{p}} = \left[ {\begin{array}{*{20}c} \pi \\ {1 - \pi } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {2/3} \\ {1/3} \\ \end{array} } \right]\) must be unique. In this example, \(\frac{\pi }{1 - \pi } = \frac{2}{1}\) can be termed as the relative price ratio between the two states, i.e., at \(t = 1\) the value of one dollar of good time is 200% greater than that of bad time. This implies that investors (the market) believe that the probability of good time is twice as many as that of bad time.
Problems
-
1.
Comment on the following statementsFootnote 17:
-
(a)
Wilmott (2007, p. 77): Assume: “(1) two stocks A and B; (2) both have the same value, same volatility and are denominated in the same currency; (3) both have call options with the same strike and expiration; (4) stock A is doubling in value every year, stock B is halving. Therefore, both call options have the same value. But which will you buy? That one stock is doubling and the other halving is irrelevant. That option prices don’t depend on the direction that the stock is going can be difficult to accept initially”.
-
(b)
Ross (1998, p. 701): “Take two stocks that both follow binomial processes and that are not perfectly correlated. Further, suppose that the stocks differ only in that one has a much higher probability of an up jump than does the other. If our analysis is to be believed, then when the stock prices of each are equal the two option values will be equal! How can this be? How can the value of an option on a stock be independent of the probability that the stock will go up?”.
-
(a)
-
2.
With zero interest rate, do the arbitrage for the following two assets:
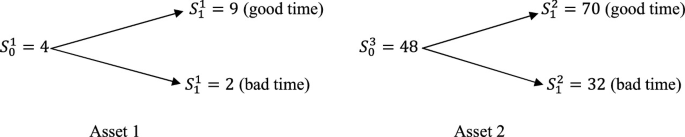
-
3.
Explain under what conditions an American put option will not be early exercised. How to use these conditions to determine the best time to liquidate a firm?
-
4.
Explain how to use the p-index to invest in stocks. What are the limitations of the p-index?
-
5.
Explain why the Black–Scholes-Merton option pricing model has: \(\frac{\partial c}{{\partial \sigma }} = \frac{\partial p}{{\partial \sigma }}\) and the binomial option pricing model has: \(\frac{\partial c}{{\partial u}} = \frac{\partial p}{{\partial u}}\) and \(\frac{\partial c}{{\partial d}} = \frac{\partial p}{{\partial d}}\).
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this chapter
Cite this chapter
Chang, KP. (2023). Derivatives and Corporate Finance. In: Corporate Finance: A Systematic Approach. Springer Texts in Business and Economics. Springer, Singapore. https://doi.org/10.1007/978-981-19-9119-6_9
Download citation
DOI: https://doi.org/10.1007/978-981-19-9119-6_9
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-9118-9
Online ISBN: 978-981-19-9119-6
eBook Packages: Economics and FinanceEconomics and Finance (R0)