Keywords

1 Introduction

At this stage, the existing research at home and abroad involves the experimental research, theoretical analysis, and finite element simulation of the natural vibration frequency of externally prestressed components, with the experimental study being the majority and the basic theory being relatively scarce [1, 2]. The conclusions drawn by the researchers based on the experiments are basically the same [3,4,5], but it was found that the experimental results are quite different from the classical kinetic theory [6,7,8,9]. To this end, some scholars have done some research in theoretical analysis. The researchers mainly use the stiffness correction method [2, 10, 11], the nonlinear calculation method [12], the equivalent stiffness method [13], and other analysis methods to explore the influence of prestress parameters on the frequency. However, due to the lack of a unified mechanism, the theoretical calculation of the influence of prestress parameters on the dynamic performance of the structure has not been consistent, and there are differences in the viewpoints that have been put forward. Many laws are diametrically opposite and inconsistent with the experimental conclusions [14].

In addition, in the classical theory, the microelement method is used to establish the equilibrium equation under uniform load, but when the external load is changed to a concentrated force, the load function on the prestressed cable is a point function, and the vibration equation is only defined at several points. In fact, the body force does not meet the applicable conditions of the micro-element method [15], so it is impossible to intercept the single body for analysis. Therefore, this paper uses the energy method to analyze the structure as a whole [16]. From the perspective of the action mechanism of the prestressed system in the steel structure, a new analysis idea is proposed, that is, the structure is first classified according to the action mechanism of the prestressed system. Then, the natural vibration frequency of each type of externally prestressed simply supported steel beams is theoretically analyzed by the method of structural dynamics, and the frequency calculation formula is finally obtained..

2 Classical Theoretical Analysis and Its Errors and Corrections

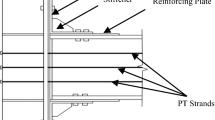
The traditional vibration theory regards the prestressed tendons as applying a pair of constant axial forces F at both ends of an ordinary simply supported beam, as shown in Fig. 1.

Fig. 1
A graph of y versus x plots an arc that originates from the origin, the left and right of which has the axial force labeled F.

Schematic diagram of bending vibration calculation of simply supported beam under the action of axial force

Full size image

According to D'Alembert's principle and the assumption of the plane section, the differential equation of beam free vibration under the action of axial force is established by neglecting the influence ofshear deformation and moment of inertia:

$$EI\frac{{\partial^{2} M(x,t)}}{{\partial x^{2} }} + F\frac{{\partial^{2} y(x,t)}}{{\partial x^{2} }} + \overline{m}\frac{{\partial^{2} y(x,t)}}{{\partial t^{2} }} = 0$$
(1)

where \(y(x,t)\), \(EI\), and \(\overline{m}\) have the same meaning as above; \(M(x,t)\)—Bending moment of steel beam section.

From Formula (1), the expression for the natural vibration frequency of a simply supported beam is:

$$\omega_{n} = (\frac{n\pi }{l})^{2} \sqrt {\frac{EI}{{\overline{m}}}} \sqrt {1 - \frac{F}{{n^{2} \frac{{EI\pi^{2} }}{{l^{2} }}}}} = \omega_{n} \sqrt {1 - \frac{F}{{n^{2} P_{c} }}}$$
(2)

In the formula: \(n = 1,2,3 \ldots\); \(l\) is the beam length; \(P_{c} = \frac{{EI\pi^{2} }}{{l^{2} }}\).

Formula 2 shows that the presence of the prestress reduces the natural bending frequency of simply supported beams, and the degree of reduction decreases with the increase of i. However, it cannot explain the experimental phenomenon that the natural frequency of precast beams increases with the increase of prestress. Some scholars use experimental data to correct the EI value in Eq. 1. Although the modified formulas are not exactly the same, they are all based on the test results to modify the stiffness, so they can be expressed as follows:

$$(EI)_{e} = (1 + \alpha )EI_{0}$$
(3)

where: \((EI)_{e}\)—the stiffness of the modified prestressed simply supported beam;

\(\alpha\)–stiffness correction factor; \((EI)_{0}\)–stiffness of the front beam body before correction.

The modified formula of stiffness is obtained by fitting the test data, and finally, the modified natural frequency calculation formula is obtained. Although a large number of researchers have revised Eq. 3, it is still empirical and not fully supported by theory, and thus not of general applicability.

3 Theoretical Analysis of the Natural Vibration Frequency of Steel Beams Based on the Action Mechanism of the Prestressed System

3.1 Prestressed Components

The mechanism of the externally prestressing system can be summarized as follows:

  1. (1)

    The prestress itself causes stress and deformation of structural members and affects the stiffness of the structure, such as the cable arch structure.

  2. (2)

    Under the action of the prestress, the prestressed carrier provides additional stiffness to the structure and adjusts its mechanical performance.

There are two manifestations of the stiffness provided by the prestressed carrier: (a) The prestressed carrier establishes the axial stiffness under the action of the prestress, and forms a new structural form with the original structure, which improves the stiffness and stability of the original structure and makes the prestressed structure more stable. As a two-force rod, the tightened cable can bear both tension and pressure, and within the elastic range, the axial stiffness of the cable has nothing to do with the cable force, such as cable-stayed structure, cable support structure, etc. (b) The second-order effect of axial force provides stiffness to the structure. The carrier does not directly provide stiffness and stability to the structure after prestressing, but when the cable is deformed perpendicular to the cable axis, stiffness is formed through the second-order effect of the central axial force (tension) of the cable. It often appears in point-supported curtain wall structures and string-supported structures.

3.2 Calculation of the Natural Vibration Frequency of the Externally Prestressed Steel Beams with Linear Coupling Cables

Based on three prefabricated members, the energy method is used to calculate the natural vibration frequency of the external prestressed members arranged with straight bars. The three assumptions presented here are consistent with the traditional Euler Bernoulli bending beam theory. In addition, the following three assumptions are added: (1) The i-th order vibration mode can be expressed as \(y_{i} = A_{i} \sin (i\uppi x/l)\sin (\omega_{i} t + \phi_{i} ), i = 1,2,3, \ldots\), where Ai, ωi, and φi are the vibration amplitude, circular frequency, and the i-th order vibration phase angle, respectively; (2) The axial force change of the steel bar is neglected; (3) The axial deformation of the beam caused by the axial force of the ribs is ignored.

3.3 Influencing Factors of Natural Vibration Frequency of Externally Prestressed Steel Beams with Linear Coupling Cables

In addition to being related to the inherent properties of steel beams such as E, I, m, and L, the natural vibration frequency f of the steel beam is also affected by three main parameters, namely, the cable force F, the eccentric distance e, and the cable cross-sectional area A in the prestressed cable. In order to directly reflect the influence of the relationship between the above-mentioned cable parameters and the natural vibration frequency, a binary surface graph of the first-order frequency variation of the linearly coupled cable-clipped steel beam with any two parameters is drawn. (Note: Because the first-order vibration is usually the most important in practical engineering, only the first-order natural frequency is considered here.)

The figure below directly reflects their effect on the first-order natural frequency of the externally prestressed steel beam.

According to Fig. 2a, the natural vibration frequency of the prestressed steel beam of the linearly coupled cable arrangement shows an increasing trend with the increase of the prestress and the eccentricity. According to the slope of the F-f and e-f curves, when other conditions are the same, the influence of the eccentricity on the natural vibration frequency of the steel beam is equivalent to the prestress. It can be seen from Fig. 2b that the natural vibration frequency of the prestressed steel beam increases with the increase of the cross-sectional area A of the cable, and the influence of the cross-sectional area on the natural vibration frequency is also equivalent to that of the prestressing force. The surface shapes of Fig. 2c are basically the same, and the natural vibration frequency of the prestressed steel beam increases gradually with the increase of the cross-sectional area and eccentricity of the cable.

Fig. 2
3 3-D graphs plot natural frequency versus eccentricity versus prestress; natural frequency versus cross-sectional area of the cable versus prestress; and natural frequency versus eccentricity versus cross-sectional area of the cable, respectively. A plots a bent rhombus, B plots a rhombus, and C plots a pyramid.

First-order frequency binary surface diagram of steel beam

Full size image

4 Analysis of Influencing Factors of Natural Vibration Frequency

Under the three cable routing methods, the effects of prestressing system parameters on the first-order frequency of prestressed simply supported steel beams were compared and analyzed. The theoretical value of the natural vibration frequency of the prestressed steel beam is calculated according to Sect. 2; according to the above finite element model, the finite element software ANSYS is used to analyze the influence of the prestress size, cable eccentricity, and the cross-sectional area of the cable on the natural vibration frequency of the prestressed steel beam, and the theoretical value and the simulated value are compared and analyzed. All analyses were performed within the linear elastic range.

4.1 Influence of Prestress on Natural Vibration Frequency

For prestressed steel beams with straight and linear coupling cables, the prestressed cables are arranged along the axis; the mid-point of the cable is anchored on the mid-span stiffener of the steel beam, 110 mm away from the neutral axis of the beam. The cross-sectional area A of the cable is taken as 139 mm2. Under different prestresses, the theoretical and simulated values of the first-order frequency of the prestressed steel beam are shown in Table 1.

Table 1 Theoretical and simulated values of the first-order frequency of prestressed steel beams under different prestresses
Full size table

According to the analysis of the chart, under different prestresses, the theoretical and simulated values of the frequency of the steel beam are basically consistent: when the linear cable routing method is adopted, the first-order frequency of the steel beam gradually increases with the increase of the prestress; when the linear coupling cable routing method is used, the first-order frequency of the steel beam gradually decreases with the increase of the prestress; when the single-broken-line cable routing method is employed, the first-order frequency of the steel beam gradually decreases with the increase of the prestress. The error of the theoretical calculation results is smaller than that of the finite element simulation results, and the error rate of the first-order frequency of the steel beam under the three cable routing methods is less than 5%.

According to the above analysis, the effect of prestress on the natural vibration frequency of steel beams is related to the way of prestressing cables. The above conclusions are explained in combination with the action mechanism of the prestressing system.

As shown in Fig. 2, when the steel beam adopts the linear coupling type cable, with the increase of the prestress, the first-order frequency of the steel beam gradually increases. In this case, due to the mid-rspan coupling between the cable and the steel beam, the cable is deformed perpendicular to the cable axis during the vibration process. Both the axial expansion of the cables and the second-order effect of the axial force increase the stiffness of the beam, and the contribution of increased stiffness to frequency is greater than the attenuation of the axial force F to frequency. Therefore, both the prestress and the frequency of the prestressed steel beams with linear coupling cables increase. And as the prestress increases gradually, the second-order effect of the axial force of the cable becomes more and more obvious, the stiffness provided to the beam body also increases continuously, and finally, the frequency of the prestressed steel beam is greater than that of the single-broken prestressed steel beam.

4.2 Effect of Eccentricity on Natural Vibration Frequency

The prestress \(F\) in the prestressed cable is 800 kN, and the cross-sectional area \(A\) of the cable is 139 mm2. Under different eccentric distances, the theoretical and simulated values of the first-order frequency of the prestressed steel beam are shown in Table 2, and the trend curve of the frequency variation of the steel beam with the eccentric distance is drawn, as shown in Table 2.

Table 2 Theoretical and simulated values of natural vibration frequencies of prestressed steel beams
Full size table

According to the above chart, under different eccentric distances, the theoretical value of the first-order frequency of the steel beam and the calculation result of the simulated value are basically consistent. The error of the theoretical calculation results is smaller than that of the finite element simulation results, and the error rate of the natural vibration frequency of the steel beam under the three cable routing methods is less than 5%.

It can be found from Fig. 2 that the first-order frequency of the prestressed steel beam increases gradually with the increase of the eccentricity under the three cable routing methods. Combining with Table 2, it can be seen that when the steel beam adopts the linear cable arrangement, as the eccentric distance of the cable increases, the simulated value of the first-order frequency of the steel beam increases from 1.87 to 6.15%, and the rate of change of the theoretical value increases from 0.80 to 4.95%. The rate of change increases continuously, and the relationship between the first-order frequency and the eccentricity is close to a quadratic function; when the steel beam adopts the linear coupling type cable, the rate of change of the simulated value of the first-order frequency of the steel beam increases from 0.70 to 5.10%, while the theoretical value increases from 0.73 to 4.55%. The rate of change increases continuously, and the relationship between the first-order frequency and the eccentricity is close to a quadratic function; when the single-broken line cable is used, the rate of change of the simulated value of the first-order frequency of the steel beam changes from 1.93 to 2.50%, while the theoretical value changes from 1.57 to 2.55%, and the rate of change is almost unchanged. The linear correlation coefficient R2 between the first-order frequency and the eccentricity is the highest among the three distribution methods, reaching 0.99, so the difference between the first-order frequency and the eccentricity is 0.99, which is closer to a linear relationship.

4.3 Influence of the Cross-Sectional Area of the Cable on Natural Vibration Frequency

The prestress F in the prestressed cable is taken as 800 kN, and the eccentricity e of the three cable routing methods is taken as 70 mm. Using steel strands with different cross-sectional areas as prestressed cables for analysis, the theoretical and simulated values of the first-order frequency of the prestressed steel beams are shown in Table 3, and the trend curve of the frequency variation of the steel beams with the cross-sectional area of the cables is drawn, as shown in Table 3.

Table 3 Theoretical and simulated values of the first-order frequency of prestressed steel beams
Full size table

Under different cross-sectional areas of the cables, the theoretical and simulated values of the natural vibration frequency of the steel beam are basically consistent. The error of the theoretical calculation results is smaller than that of the finite element simulation results, and the error rate of the natural vibration frequency of the steel beam under the three cable routing methods is less than 5%.

According to Table 3, when the cross-sectional area of the cable gradually increases from 54.8 mm2 to 285 mm2, the change rate of the simulated value of the first-order frequency of the linear cable prestressed steel beam decreases from 1.00 to 0.71%, and that of the theoretical value decreases from 0.91 to 0.88%; the rate of change of the simulated value of the first-order frequency of the linear coupling type cable prestressed steel beam is reduced from 0.41 to 0.27%, and that of the theoretical value is reduced from 0.84 to 0.80%; the rate of change of the simulated value of the first-order frequency of the linear cable prestressed steel beam is reduced from 1.05 to 0.69%, and that of the theoretical value is reduced from 1.94 to 1.83%. Therefore, the first-order frequencies of the prestressed steel beams in the three cable routing methods all increase with the increase of the cross-sectional area of the cables, and the rate of change gradually decreases.

5 Conclusion

  1. (1)

    The size of the prestress, the eccentric distance, and the cross-sectional area of the cable will have a certain influence on the natural vibration frequency of the prestressed simply supported steel beam;

  2. (2)

    The calculation formula of the natural vibration frequency of the externally prestressed simply supported steel beam deduced in this paper can accurately obtain the natural vibration frequency of the structure. The variation law of the first-order frequency of the steel beam reflected by the formula with the prestress is basically consistent with the finite element simulation results, and has good calculation accuracy, which can provide a certain reference for engineering applications;

  3. (3)

    The effect of prestress on the natural vibration frequency of steel beams is related to the way of prestressing cables. When the prestressed steel girder adopts linear cable distribution, the frequency of the steel girder decreases gradually with the increase of the prestress; when the prestressed steel girder adopts linear coupling cable distribution, with the increase of the prestress, the frequency of the steel beam increases gradually; when the prestressed steel beam adopts the single broken line cable, with the increase of the prestress, the frequency of the steel beam gradually decreases;

  4. (4)

    The natural vibration frequency of the externally prestressed simply supported steel beam increases with the increase of the eccentric distance;

  5. (5)

    The natural vibration frequency of the externally prestressed simply supported steel beam increases with the increase of the cross-sectional area of the cable.