Keywords

1 Introduction

The side-hole projection theory was used in the early 1990s in Europe and the USA for practical engineering purposes. Liao et al. [1] proposed to identify the intersection point as the pile length by fitting the initial wave of the depth-time curve to two line segments via Snell’s law. With the continuous development of the parallel seismic methods of pile foundation inspection technology in recent years, domestic scholars have scrambled to study and establish simplified calculation models and correction methods [2,3,4,5], there are now relevant specification documents applied to pile foundation inspection [6].

Traditional anchor testing methods rely on equipment such as displacement convergence meters, roof separation indicators and drawing meters, but these destructive testing methods cannot be promoted due to the irreversible damage they cause to the support structure [7]. With the development of non-destructive testing technology, the corresponding techniques are gradually being applied to anchor detection. Common detection methods include the stress wave method, ultrasonic method, etc. [8, 9]. However, as the working conditions of anchor anchoring system are more complex compared with foundation piles, the identification of elastic wave reflection signal is difficult, and the accuracy of identifying the length of long anchor bar in complex surrounding rock conditions is extremely limited, so the quality control of anchor bar construction is still restricted by the detection means. In this study, ABAQUS was used to simulate the application of the parallel seismic methods in tunnel anchor length detection and to verify its feasibility.

2 Principle of Parallel Seismic Methods

2.1 Basic Principle

Parallel seismic methods were first used as a method to determine the length of foundation piles for foundation integrity testing [10]. According to Fermat’s principle, waves always propagate along the path with the shortest duration, and this principle provides the mathematical basis for the path and duration of initial wave propagation. According to Snell’s law, stress wave propagation along a pile foundation produces a refracted longitudinal wave and a refracted transverse wave after shock-excitation. The elastic waves conducted within the pile can be approximated as plane waves due to the large difference in wave impedance at the pile boundaries, which is in line with the theory of one-dimensional wave conduction. The geophone in the side bore will be the first to receive the elastic wave conducted from the pile [11, 12].

The tunnel anchorage body consists of metal anchors, and grip-coated mortar together and can be seen as an ideal one-dimensional anchor bar. The exposed end of the anchor rod is excited to produce a compressional (P-wave) or shear (S-wave) wave, which is transmitted down the anchor solid and produces a refracted longitudinal (PP) and transverse (PS) refraction wave inside the anchor bar in the bottom, with sine value of refraction angle equal to the ratio of the stress wave velocity of the surrounding rock to that of the anchor solid. First, stress wave signals can be collected at different depths by drilling a bypass hole near the anchor bar or by using a geophone placed in an adjacent ungrouted borehole. The equation for the first PS wave duration at any depth z above the point Q (depth is L + Dtanβ, L is the pile length and D is the side hole distance) in the side borehole, without considering the effect of 3D effects on the pile, is shown in Eqs. (1–3).

$$m = \frac{{V_{pp} }}{{V_{ss} }} = \frac{1}{sin\beta }$$
(1)
$$Z_{s} = {\text{D}}\tan \beta = \frac{D}{{\sqrt {m^{2} - 1} }}$$
(2)
$$t_{s} = \frac{{z - z_{s} }}{{V_{pp} }} + \frac{D}{{V_{ss} cos\beta }} = \frac{z}{{V_{pp} }} + \frac{{{\text{D}}\sqrt {m^{2} - 1} }}{{V_{pp} }}$$
(3)

where D is the net horizontal spacing between the side of the anchor solid and the side hole, hereinafter referred to as the borehole distance; Vpp is the one-dimensional P-wave velocity of the anchor solid; Vss is the S-wave velocity of the surrounding rock where the anchor solid is located; β is the angle of projection of the stress wave from the anchor solid to the surrounding rock; Z is the depth of burial of the geophone; Zs is the propagation depth of the S-wave in the surrounding rock.

The equation for the first PS wave duration at any depth z in the borehole below point Q is shown in (4), where L is the anchor length.

$$t_{s} = \frac{L}{{V_{pp} }} + \frac{{\sqrt {D^{2} + \left( {z - L} \right)^{2} } }}{{V_{ss} }} = \frac{L}{{V_{pp} }} + \frac{z - L}{{V_{ss} }}\sqrt {1 + \left( {\frac{D}{z - L}} \right)^{2} }$$
(4)

It can be seen from Eq. (4) that the maximum error of \(\sqrt {1 + \left( {\frac{D}{z - L}} \right)^{2} } \approx 1\) is no greater than 2% for z-L ≥ 5D, which can be approximated by writing it in a form independent of D as shown in Eq. (5).

$$t_{s} = \frac{z}{{V_{ss} }} - \frac{m - 1}{m} \cdot \frac{L}{{V_{ss} }}$$
(5)

When z-L ≥ 5D, the effect of the side hole distance D on the first PS wave time-depth relationship is small, and the wave time-depth relationship corresponding to different side hole distances can be approximated as a straight line (Fig. 1).

Fig. 1
A model diagram of a side hole, anchor solids, and surrounding rock. The necessary labels are marked.

A simplified computational model for the parallel seismic methods

Full size image

2.2 Calculation of Anchor Length

As can be seen from Sect. 2.1, when z-L ≤ 5D, the t ~ z relationship of the first PS wave is a straight line with a slope of \(1/V_{pp}\), i.e. the time-depth line inside the anchor; when z-L ≥ 5D, the t ~ z relationship is a straight line with a slope \(1/V_{ss}\), i.e. the time-depth line of the surrounding rock at the bottom of the anchor. The formula for calculating the depth of the anchor is Eq. (7).

$$L_{c} = D\sqrt {\left( {m + 1} \right)/\left( {m - 1} \right)}$$
(6)
$$L = z_{i} - L_{c}$$
(7)

where, zi is the depth of the intersection of the time-depth line within the anchor bar and the time-depth line of the surrounding rock at the bottom of the bar; When D = 0, L = zi means that the excitation point is at the exposed end of the anchor bar and the side hole is immediately adjacent to the anchor solid. If the time-depth line in the anchor bar is translated past the origin, the depth of its intersection with the time-depth line at the bottom of the bar can be regarded as the length of the anchor bar. The above method is called the translation line intersection method, also called the intersection correction method, and is illustrated in Fig. 2.

Fig. 2
A schematic diagram is shaped like the fourth quadrant of a graph. The depicted dotted lines are l subscript 1, l dash subscript 1, and l subscript 2, while the depicted solid lines are z subscript 0, z subscript f, and z subscript i.

Schematic diagram of the translating line plus dot method

Full size image

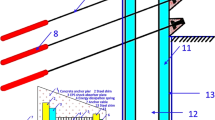
3 Non-destructive Testing Method for Tunnel Anchor Lengths

Based on the above theory and the more refined theory of non-destructive testing of anchor bar anchorage quality (one-dimensional bar) [13], a non-destructive testing method for tunnel anchor length is proposed, as shown in Fig. 3.

Fig. 3
An illustration of the tunnel anchor length detection device includes, mainframe, excitation wave receiver, anchor bar and anchor solid, and transmissive wave receiver.

Tunnel anchor length detection device

Full size image

The detection device consists of an excitation hammer, an excitation wave receiver, a transmissive wave receiver and a mainframe. To detect, a PVC pipe of suitable size is embedded in the borehole, the transmittance receiver is fed into the bottom of the hole, then the exposed end of the anchor is tapped and the signal is collected, followed by lifting the receiver at equal intervals and repeating the tap to collect the signal. The detection host analyses the anchor length by recording the time difference between the signals received by the excitation and transmission wave receivers to create a time-depth curve.

4 Simulation Analysis of Abaqus-Based Tunnel Anchor Length Detection

4.1 Finite Element Modelling

ABAQUS software was used to build the anchor-anchor solid-surrounding rock model. The total length of the model is preset to was 6 m, the length of the anchor solids was 4 m, the diameter was 0.4 m and the diameter of the anchors was 4 cm. According to the one-dimensional elastic wave theory, the wave velocity in the anchor and the surrounding rock is calculated by Eq. (8).

$$V = \sqrt {\frac{E}{\rho }}$$
(8)

The material parameters for the anchors and the surrounding rock are defined with reference to《Design specification of highway tunnel》, as shown in Table 1.

Table 1 Formatting sections, subsections and subsubsections
Full size table

The Moore-Coulomb model was chosen for the surrounding rock materials model, with an internal friction angle of 55° and cohesion of 2.0 MPa. The anchor bar selects dynamic surface contact, and the contact algorithm is a symmetric function method [14], that is, at each node, first check whether the node penetrates the main interface, if it does not, no processing is done; If there is penetration, a larger contact force (the magnitude of the force is determined by the stiffness of the main surface and the depth of penetration) is applied between the main interface and the node, which can be seen as adding a spring with greater stiffness between the main and secondary interfaces to reduce the penetration degree of the primary surface of the secondary node. The boundary conditions are set both at the bottom of the anchor and around the anchor solid. The bottom end of the anchor is set to “fully fixed” as it will not be displaced; around the anchor, the displacement in the X and Y directions is constrained and set to 0. The solids are meshed and divided into hexahedral meshes in a swept form.

The excitation method uses uniform excitation force, using the excitation hammer to produce uniform transient excitation, the excitation force pulse is a half-sine pulse [15], the size of P = P0sinω t, 0 < t < tc, P0 is the peak excitation force, take 10 N, t is the excitation force action time, take 1 × e−3 s, the form of pulse force is uniform force, as shown in Fig. 4. The vertical excitation point is located at the exposed end of the anchor bar and the measurement holes are placed 0.5 m from the edge of the anchor bar.

Fig. 4
A dome shaped plots magnitude versus time curve for loading frequency.

Loading frequency

Full size image

4.2 Point Wave Speed Processing

The results of the wave speed distribution at the point after submission of the above model are shown in Fig. 5. The results show that the stress propagates in the form of fluctuations towards the bottom of the anchor and bends back after reflection from the surrounding rock at the bottom of the anchor. The generation of fluctuations indicates that the finite element model developed is reasonable. The variation of velocity with time on a straight line at 20 cm from the edge of the anchor bar was extracted and the velocity-time curve at 0.5 m from the top of the anchor bar is shown in Fig. 6.

Fig. 5
A point wave distribution spectrum depicts a horizontal band of varying magnitude points. The V magnitude is 0 up to half of the band while it increases towards the right.

Point wave speed distribution

Full size image
Fig. 6
A line graph plots point wave speed versus time. The curve peaks at 1.1, 3.75 and the values decline gradually after.

Point wave speed plotted against time

Full size image

4.3 Linear Fit Analysis

A measurement point was placed at 0.5 m intervals and time-velocity data was extracted from each measurement point and the waveforms at each depth were plotted as shown in Fig. 7. The peak points were automatically identified and extracted using Matlab software and a linear fit was performed, the results of which are shown in Fig. 8. The slopes of the straight lines above 4 m and below 4 m were 5090.18 and 3576.4 respectively, with errors of 1.19 and 2.3% compared to the calculated wave speeds. The two straight lines in the graph are compared at a depth of 4.06 m with an error of 1.5%.

Fig. 7
A line graph plots depth versus time depicts the waveform plots of increasing horizontal length as we move from top to bottom.

Waveform plots at different depths

Full size image
Fig. 8
A line graph plots depth versus time. The curve is a nearly straight line with a negative slope.

Peak point fitted straight line

Full size image

The analysis of the causes of errors consists of two main aspects. For one, the condition for viewing the time-depth curve as a straight line in the envelope is Z-L ≥ 5D, but when 0 < Z-L < 5D, the time-depth curve is a hyperbola and approximates this part as a straight line yields a large wave speed in the envelope. Secondly, the overall translation of the time-depth curve above 4 m to the right is due to the presence of the side hole distance, so the translation line intersection method has been proposed to correct this error [16]. The errors arising from the above-mentioned causes have little effect on the measurement of anchor lengths and it is therefore theoretically feasible to use the parallel seismic methods to detect the length of tunnel anchors.

5 Conclusion

A comprehensive analysis of the above computational derivations and simulation results resulted in the conclusion that the parallel seismic methods are theoretically feasible for the verification of anchor lengths. During the construction of the support structure, the existing boreholes can be used to test the surrounding anchor structure. At the end of construction, the method can still be used as an effective evaluation tool for post-facto quality surveys, breaking the deadlock of difficult to detect anchor lengths and difficult to identify at the end of construction, and providing strong technical support for anchor anchoring quality control.