Abstract
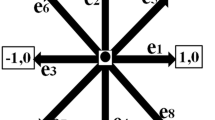
This article details a novel numerical algorithm to simulate compressible flow in the supersonic regime using the kinetic theory based lattice Boltzmann equation (LBE) method. In order to achieve higher-order accuracy, a fifth-order weighted essentially non-oscillatory (WENO) scheme with third-order Runge-Kutta (RK3) time integration is utilized. The LBE is solved using finite-differences on regular lattice structures with the discrete Bhatnager-Gross-Krook (BGK) approximation. A discrete velocity model given by Kataoka and Tsutahara (T. Kataoka and M. Tsutahara. Lattice Boltzmann method for the compressible Euler equations. Physical Review E, 69(5):056702, 2004) has been used, along with additional dissipation and artificial viscosity terms in order to account for the high Mach number problems. The most commonly studied benchmark two-dimensional, forward-facing step problem with a step-height of 0.2 and Mach number (Ma = 3) is used for validation. Further, the effect of change in the step-height on various parameters such as shock stand-off distance, Mach stems height, and triple points location are studied.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
Victor Sofonea, A Lamura, G Gonnella, and A Cristea. Finite-difference lattice Boltzmann model with flux limiters for liquid-vapor systems. Physical Review E, 70(4):046702, 2004.
Dhiraj V Patil and KN Lakshmisha. Finite volume TVD formulation of lattice Boltzmann simulation on unstructured mesh. Journal of Computational Physics, 228(14):5262–5279, 2009.
Misun Min and Taehun Lee. A spectral-element discontinuous galerkin lattice Boltzmann method for nearly incompressible flows. Journal of Computational Physics, 230(1):245–259, 2011.
Timm Krüger, Halim Kusumaatmaja, Alexandr Kuzmin, Orest Shardt, Goncalo Silva, and Erlend Magnus Viggen. The lattice Boltzmann method. Springer International Publishing, 10(978-3):4–15, 2017.
Cyrus K Aidun and Jonathan R Clausen. Lattice-Boltzmann method for complex flows. Annual review of Fluid Mechanics, 42:439–472, 2010.
XF Pan, Aiguo Xu, Guangcai Zhang, and Song Jiang. Lattice Boltzmann approach to high-speed compressible flows. International Journal of Modern Physics C, 18(11):1747–1764, 2007.
Yanbiao Gan, Aiguo Xu, Guangcai Zhang, Xijun Yu, and Yingjun Li. Two-dimensional lattice Boltzmann model for compressible flows with high Mach number. Physica A: Statistical Mechanics and its Applications, 387(8-9):1721–1732, 2008.
Huidan Yu and Kaihua Zhao. Lattice Boltzmann method for compressible flows with high Mach numbers. Physical Review E, 61(4):3867, 2000.
Guang-Shan Jiang and Chi-Wang Shu. Efficient implementation of weighted ENO schemes. Journal of Computational Physics, 126(1):202–228, 1996.
Dinshaw S Balsara and Chi-Wang Shu. Monotonicity preserving weighted essentially non-oscillatory schemes with increasingly high order of accuracy. Journal of Computational Physics, 160(2):405–452, 2000.
Oliver Friedrich. Weighted essentially non-oscillatory schemes for the interpolation of mean values on unstructured grids. Journal of Computational Physics, 144(1):194–212, 1998.
Jing Shi, Changqing Hu, and Chi-Wang Shu. A technique of treating negative weights in WENO schemes. Journal of Computational Physics, 175(1):108–127, 2002.
Chi-Wang Shu. Essentially non-oscillatory and weighted essentially non-oscillatory schemes for hyperbolic conservation laws. pages 325–432. Springer, 1998.
Xiaoyi He and Li-Shi Luo. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Physical review E, 56(6):6811, 1997.
Xiaoyi He and Li-Shi Luo. A priori derivation of the lattice Boltzmann equation. Physical Review E, 55(6):R6333, 1997.
Takeshi Kataoka and Michihisa Tsutahara. Lattice Boltzmann method for the compressible Euler equations. Physical Review E, 69(5):056702, 2004.
Paul Woodward and Phillip Colella. The numerical simulation of two-dimensional fluid flow with strong shocks. Journal of Computational Physics, 54(1):115–173, 1984.
You Li, Xiao-Dong Niu, Hai-Zhuan Yuan, Adnan Khan, and Xiang Li. A numerical study for WENO scheme-based on different lattice Boltzmann flux solver for compressible flows. Acta Mechanica Sinica, 34(6):995–1014, 2018.
Acknowledgements
Authors hereby acknowledge the support of ‘AnantGanak: HPC facility at IIT Dharwad’, to enable them to carry the reported work. S.G. Nayak and D.V. Patil acknowledge the support of ISRO-RESPOND and VSSC for project ‘RESPOND-VSSC002’.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Shirsat, A.U., Nayak, S.G., Patil, D.V. (2023). Supersonic Inviscid Flow Over 2D Forward-Facing Step Using RK3 + WENO and Finite-Difference Lattice Boltzmann Equation Method. In: Bhattacharyya, S., Chattopadhyay, H. (eds) Fluid Mechanics and Fluid Power (Vol. 1). FMFP 2021. Lecture Notes in Mechanical Engineering. Springer, Singapore. https://doi.org/10.1007/978-981-19-7055-9_16
Download citation
DOI: https://doi.org/10.1007/978-981-19-7055-9_16
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-7054-2
Online ISBN: 978-981-19-7055-9
eBook Packages: EngineeringEngineering (R0)