Abstract
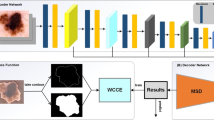
This paper proposes a novel loss function inspired by the Tversky-Kahneman probability weighting function to effectively deal with medical image segmentation tasks. The proposed loss, which is called Tversky-Kahneman loss function, is assessed on the official Skin Lesion datasets of the ISIC 2017 and ISIC 2018 Challenge. To evaluate our new loss function, we propose modified U-Net-based model to obtain quantitative results in Dice score and Jaccard index. Various experiments indicate that our new loss function provides a more promising and time-saving performance than other loss functions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Szeliski R (2010) Computer vision: algorithms and applications. Springer
Bansal J (2019) Particle swarm optimization. Evolutionary and swarm intelligence algorithms, pp 11–23. https://doi.org/10.1007/978-3-319-91341-4_2. ISBN 978-3-319-91339-1
Kumar S, Sharma B, Sharma V, Sharma H, Bansal J (2018) Plant leaf disease identification using exponential spider monkey optimization. Sustain Comput Inf Syst 28. https://doi.org/10.1016/j.suscom.2018.10.004
Bansal J, Sharma H (2012) Cognitive learning in differential evolution and its application to model order reduction problem for single-input single-output systems. Mem Comput 4. https://doi.org/10.1007/s12293-012-0089-8
Jafari MH, Karimi N, Nasr-Esfahani E, Samavi S, Soroushmehr SMR, Ward K, Najarian K (2016) Skin lesion segmentation in clinical images using deep learning. In: 2016 23rd international conference on pattern recognition (ICPR). https://doi.org/10.1109/ICPR.2016.7899656
Wolterink JM, Leiner T, Viergever MA, Išgum I (2017) Dilated convolutional neural networks for cardiovascular MR segmentation in congenital heart disease. Lecture Notes in Computer Science. https://doi.org/10.1007/978-3-319-52280-7-9
Long J, Shelhamer E, Darrell T (2015) Fully convolutional networks for semantic segmentation. arXiv
Lin G, Shen C, van dan Hengel A, Reid I (2016) Efficient piecewise training of deep structured models for semantic segmentation. arXiv
Ronneberger O, Fischer P, Brox T (2015) U-net: convolutional networks for biomedical image segmentation. arXiv
Zhou X-Y, Shen M, Riga CV, Yang G-Z, Lee S-L (2017) Focal FCN: towards small object segmentation with limited training data. CoRR
Tran PV (2017) A fully convolutional neural network for cardiac segmentation in short-axis MRI. arXiv
Mumford D, Shah J (1989) Optimal approximations by piecewise smooth functions and associated variational problems. Commun Pure Appl Math, pp 577–685
Chan TF, Vese LA (2001) Active contours without edges. IEEE Trans Image Process, pp 266–277. https://doi.org/10.1109/83.902291
Chambolle A, Pock T (2011) A first-order primal-dual algorithm for convex problems with applications to imaging. J Math Imaging Vis. https://doi.org/10.1007/s10851-010-0251-1
Trinh MN, Nguyen NT, Tran TT, Pham VT (2021) A semi-supervised deep learning-based approach with multiphase active contour loss for left ventricle segmentation from CMR images. In: The 3rd international conference on sustainable computing SUSCOM-2021
Salehi SSM, Erdogmus D, Gholipour A (2017) Tversky loss function for image segmentation using 3D fully convolutional deep networks. arXiv
Abraham N, Khan NM (2018) A novel focal tversky loss function with improved attention U-Net for lesion segmentation. arXiv
Zhao H, Shi J, Qi X, Wang X (2017) Pyramid scene parsing network, arXiv, Jiaya Jia
Chen L-C, Papandreou G, Kokkinos I, Murphy K, Yuille AL (2017) DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs. arXiv
Chen L-C, Papandreou G, Schroff F, Adam H (2017) Rethinking atrous convolution for semantic image segmentation. arXiv
Wang F, Jiang M, Qian C, Yang S, Li C, Zhang H, Wang X, Tang X (2017) Residual attention network for image classification. CoRR
Wang Y, Ni D, Dou H, Hu X, Zhu L, Yang X, Xu M, Qin J, Heng P-A, Wang T (2019) Deep attentive features for prostate segmentation in 3D transrectal ultrasound. IEEE Trans Med Imaging, pp 2768–2778. https://doi.org/10.1109/tmi.2019.2913184
Jo S, Ozan O, Michiel S, Mattias H, Bernhard K, Ben G, Daniel R (2019) Attention gated networks: learning to leverage salient regions in medical images. arXiv
Ange L, Shuyue G, Murray L (2020) DC-UNet: rethinking the U-Net architecture with dual channel efficient CNN for medical images segmentation. arXiv
Ingersoll, J (2008) Non-monotonicity of the Tversky-Kahneman probability-weighting function: a cautionary note. Eur Finan Manag, pp 385–390. https://doi.org/10.1111/j.1468-036X.2007.00439.x
Takemura K, Murakami H (2016) Probability weighting functions derived from hyperbolic time discounting: psychophysical models and their individual level testing. Front Psychol 7. https://doi.org/10.3389/fpsyg.2016.00778. ISSN: 1664-1078
Dozat T (2016) Incorporating Nesterov momentum into Adam
Acknowledgements
This research is funded by the Hanoi University of Science and Technology (HUST) under project number T2021-PC-005. Minh-Nhat Trinh was funded by Vingroup JSC and supported by the Master, Ph.D. Scholarship Program of Vingroup Innovation Foundation (VINIF), Institute of Big Data, code VINIF.2021.ThS.33.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Nham, DHN., Trinh, MN., Pham, VT., Tran, TT. (2023). Tversky-Kahneman: A New Loss Function for Skin Lesion Image Segmentation. In: Saraswat, M., Chowdhury, C., Kumar Mandal, C., Gandomi, A.H. (eds) Proceedings of International Conference on Data Science and Applications. Lecture Notes in Networks and Systems, vol 551. Springer, Singapore. https://doi.org/10.1007/978-981-19-6631-6_14
Download citation
DOI: https://doi.org/10.1007/978-981-19-6631-6_14
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-19-6630-9
Online ISBN: 978-981-19-6631-6
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)