1 Introduction

The ocean plays a vital role in regulating global climate change, About ~30% of total emissions since the pre-industrial period has been stored in the ocean, However, about 50% of the oceanic uptake of anthropogenic carbon takes place in the Southern Ocean. It dominates the global heat and carbon dioxide absorption, therefore, many scientists regard the Southern Ocean as the main research region. The “Southern Ocean” (\(<35\,^{\circ }\)S) was proposed by scientists around 2000 and was determined to be the fifth largest ocean in the world. It is the only ocean that completely surrounds the earth but is not divided by continents. It has important differences from ocean currents in the Pacific, Indian and Atlantic oceans—Antarctic Circumpolar Current (ACC). Moreover, the Southern Ocean is also an important region for global carbon absorption and release. Before industrial time, due to the influence of upwelling in the Southern Ocean, it has become a major carbon source region [6]. With the influence of human activities, the atmospheric pressure gradient shifted and turned into a carbon sink region. In the following section, We use the SOCAT dataset to build a Feedfoward neural network (FFNN), based on this network we reconstruct the Southern Ocean pCO2 data and calculate the CO2 flux changes in the region, compare with other method, Our algorithm is compared with two neural network algorithms and has a smaller root mean square error.

Fig. 1
figure 1

1998-2018 SOCAT data observation heat map

Full size image

1.1 Observations of pCO2 in Southern Ocean

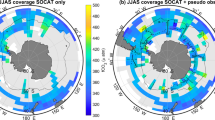
Many data of the carbonate system can only be obtained by in-situ measurement. Due to the harsh environment of the Southern Ocean, the data collection is lacking. For sea surface data, through the continuous efforts of the scientists, the Surface Ocean CO2 Atlas [13] has complies and quality control of ship data, fixed-point observation data, and drifting buoy data to formed a relatively complete observation data set (Fig. 1). This data set contains the pCO2 data which can be used to calculate the sea-air carbon dioxide flux. We will use this database as the truth value to construct our neural network and reconstruct the pCO2 gridded data of the entire Southern Ocean.

1.2 Comparison of Reconstruction pCO2 Data

The results obtained by some traditional atmospheric inversions algorithms are greatly affected by the amount of observational data [17, 20]. Some spatial and temporal interpolations are based on empirical relationships between carbon dioxide and alternative variables, and are mainly concentrated in areas with relatively rich observations.

Neural network approaches have been frequently used in the reconstruction of surface pCO2 in recent years. To recreate the pCO2 data of the Southern Ocean, Gregor et al. employed a support vector machine (SVM) and a random forest (RF). The root-mean-square errors (RMSEs) were 16.45 \(\mu \)atm and 24.04 \(\mu \)atm, respectively. Meanwhile, Landschutzer et al. [11] created the SOM-FFNN method by combining a self-organizing map (SOM) with a feedforward neural network (FFNN) to recreate pCO2 data from the Southern Ocean. Sea surface temperature (SST), sea surface salinity (SSS), Mixed Layer Depth (MLD), chlorophyll concentration (CHL), and other metrics are used as inputs. The study shows that during the period 1980-2000, the Southern Ocean carbon sink has remained stagnant or even weakened, and continued to increase after 2002. Both data products showed good interannual and seasonal cyclical changes, but compare with the traditional machine learning algorithm (SVM and RF), SOM–FFNN show better performance. Denvil-Sommer et al. [3] employed the Laboratory of Climate and Environmental Sciences (LSCE)–FFNN method to reconstruct global pCO2 data, which maintained consistency with observational results. However, compared with the observed data, the Southern Ocean’s reconstructed data has a larger error than other regions with more in situ observations.

In this chapter, we use the Surface Ocean CO2 ATLAS (SOCAT V.6) data from 1998 to 2018 in the Southern Ocean, we applied the (CA)–FFNN method to reconstruct the monthly and \(1\,^{\circ }\times 1\,^{\circ }\) pCO2 data of the Southern Ocean. Due to FFNN produces more stable data in sparse areas [20], and interpolates the data with small deviation [12], we use this method to reconstruct the Southern Ocean regional data. The procedure is separated into two parts. First, each parameter’s correlation index is calculated and arranged. Second, the pCO2 data in the southern ocean blank area was interpolated using a relational model employing parameters with reasonably strong correlation coefficients as input variables of the FFNN. The current scenario, in which stations with less observation data have larger RMSE values, is improved by this strategy. As a result, this method might be used to recreate regional data. Finally, we looked at pCO2 fluctuations in the Southern Ocean on a seasonal, interannual, and interdecadal scale.

2 Data and Methods

2.1 Data

The parameters used in the CA method included SST , SST anomaly (SSTA), SSS, and SSS anomaly (SSSA); these parameters were all from the gridded dataset of Global Ocean Heat Content Change [2], while anomaly data were obtained by subtracting the average data values from the climatic state data of each month. Chlorophyll concentration (Chl-a) were based on satellite remote sensing data from the European Space Agency’s Global Color Project, while MLD data were obtained from the French Institute of Marine Development. The u- and v- components of the wind field at 10 meters above sea level (a.s.l.) were taken from the European Centre for Medium-Range Weather Forecasts. All these data except MLD are monthly averages over a \(1\,^{\circ }\times 1\,^{\circ }\) Lat/Lon box. MLD data is monthly averages over \(0.5\,^{\circ }\times 0.5\,^{\circ }\).

In this chapter, we convert the fCO2 data in the SOCAT data set to pCO2 data as the training set and test set of FFNN. Transformation relationship between fCO2 and pCO2 is as follows [10]:

$$\begin{aligned} f\text {CO}_{2} = p\text {CO}_{2} \cdot \exp \left( p \cdot \frac{B + 2\delta }{R \times T_{\text {subskin}}} \right) \end{aligned}$$
(1)

where p is the atmospheric pressure (Pa), R is the gas constant (8.314 J K-1 mol-1), SST is the sea surface temperature (K), Tsubskin is the subskin temperature and B and \(\delta \) are the correction coefficients, which are calculated as:

$$\begin{aligned} T_{\text {subskin}}\ = \ \text {SST} + 0.17 \end{aligned}$$
(2)
$$\begin{aligned} B\left( \frac{m^{3}}{\text {mol}} \right) = ( - 1636.75 + 12.0408SST - 3.27957 \times 10^{- 2}\text {SS}T^{2} + 3.16528 \times 10^{- 5}\text {SST}^{3}) \times 10^{- 6} \end{aligned}$$
(3)
$$\begin{aligned} \delta \left( \frac{m^{3}}{\text {mol}} \right) = \left( 57.7 - 0.118T_{\text {subskin}} \right) \times 10^{- 6} \end{aligned}$$
(4)

The partial pressure of atmospheric CO2 was calculated by the following formula [14]:

$$\begin{aligned} \text {pCO}_{2a} = {\ \text {xCO}}_{2}\left[P_{\text {eq}} - \text {VP}\left( H_{2}O \right) \right]\end{aligned}$$
(5)

where xCO2 is the dry air mixing ratio of atmospheric CO2. The relevant data are collected from the reference data of marine boundary layer in the Earth System Research Laboratory of the National Oceanic and Atmospheric Administration (NOAA). Additionally, Peq is the pressure at equilibrium, and VP (H2O) is the steam of seawater at a given temperature [8]

$$\begin{aligned} \text {VP} = 0.61121 \times e^{\left( 18.678 - \frac{T_{\text {subskin}}}{234.5} \right) \times \frac{T_{\text {subskin}}}{257.14 + T_{\text {subskin}}}} \end{aligned}$$
(6)

where the \(T_{\text {subskin}}\) is subskin temperature.

In order to reduce the complexity of calculation of too large data set on neural network learning, we use Eq. 7 to normalize all data.

$$\begin{aligned} x^{'} = \frac{x - \min \left( x \right) }{\max \left( x \right) - \min \left( x \right) } \end{aligned}$$
(7)

where x is actual value, min(x) is the minimum value of x, max(x) is the maximum value of x.

Since the Chl-a data in this study did not include relevant records before the launch of SeaWiFS in 1997, our research period was from 1998 to 2018. The spatial resolution of all parameter data was \(1\,^{\circ } \times 1\,^{\circ }\). Longitude (Lon) and latitude (Lat) are in \(360\,^{\circ }\) and \(180\,^{\circ }\) coordinate systems, and trigonometric conversion functions were used to ensure continuity and normalization.

2.2 Nonlinear Neural Network Model for the pCO2 Reconstruction in the Southern Ocean

We use Equations 8 and 9 to calculate the correlation coefficient, and build a covariance matrix between pCO2 and other collected data, as shown in Fig. 3.

$$\begin{aligned} \text {Cov}\left. (,Y \right. ) = \ E\left[\left( X - u_{x} \right) \left( Y - u_{y} \right) \right]\end{aligned}$$
(8)
$$\begin{aligned} \rho = \frac{\text {Cov}(X,Y)}{\beta _{x}\beta _{y}} \end{aligned}$$
(9)

where \(u\) is the mean of the value, \(\beta \ \)is standard deviation of the value, Cov(X, Y) is the calculated covariance matrix, and \(\rho \) is the correlation coefficient.

We use the parameters with correlation coefficients > 0.1 as the input parameters, considering the relevance of chemical effects between SST and pCO2 [18], We still use SST as an input parameter. After correlation analysis, the selected parameters were the SST, SSSA, MLD, CHL, the u-component (U) of the sea surface wind field, and the partial pressure of atmospheric \(CO_2\) (pCO2a). The established correlation equations between pCO2 and the main parameters are summarized in Eq. 10.

$$\begin{aligned} {p\text {CO}}_{2} = f \begin{pmatrix} \text {SST},\text {SSSA},\text {CHL},\text {MLD}, \\ U,\text {aCO}_{2},\text {Lon},\text {Lat} \\ \end{pmatrix} \end{aligned}$$
(10)
Fig. 2
figure 2

The Structure of our FFNN, The gray square is the dropout layer and dropout rate is 0.5, blue square is input layer, yellow square is hidden layer, green square is output layer

Full size image
Fig. 3
figure 3

Matrix of correlation coefficients. The correlation coefficient value of the x-axis and y-axis parameters is represented by each colored box. The value of the p\(CO_2\) correlation coefficient with other parameters is contained within the blue box

Full size image

A nonlinear regression model was built using the FFNN. Although an FFNN’s output data improves and becomes more accurate as the number of layers and neurons in the FFNN grows, the model’s size is also determined by the amount of data utilized for model training. Because there is less observational data for the Southern Ocean than for other regions, we built a simple FFNN structure, the neutral network structure of which is shown in Fig. 2. The final model at Step 2 has eight layers (six hidden layers), and the numbers on the figure represent the size of the tensor input to each layer. A gray square represents the dropout layer, and the dropout rate is 0.5. The hyperparameters of the neural network were determined using k-fold cross-validation (Fig. 4).

The data were divided into 75%/25% portions used for training/testing sets. The neural network consists of eight layers, and the middle layer had six completely connected hidden layers, we added three dropout layers and gave each layer’s dropout ratio 0.5 to prevent the FFNN from overfitting. Through many tests and detailed analyses, the hyperbolic tangent (Tanh) was selected as the activation function of the neuron, and the using the mean squared error (MSE) as the loss function:

$$\begin{aligned} MSE = \frac{1}{N}\sum _{i = 1}^{N}\left( \text {observed}_{i} - \text {predicted}_{i} \right) ^{2} \end{aligned}$$
(11)

where observedi is the observation data, and predictedi is the data predicted by the FFNN model, and we using RMSProp as the optimization function [21].

Fig. 4
figure 4

k-Fold cross-validation, which was divided into four folds in this study, with 25% data for testing and the rest for training to create the best neural network. The yellow shape represents test data, whereas the blue shape represents train data

Full size image

In order to control the amount of information, we adjusted the adaptive learning rate. The CA–FFNN was then formed by combining a main factor analysis and based on the parameters, we build a FFNN structure and get a nonlinear regression model through training.

2.3 Calculation of Carbon Dioxide Flux in the Southern Ocean

The formula for calculating the carbon dioxide flux at the air-sea interface is [29] :

$$\begin{aligned} F = K \cdot \mathrm {\Delta }{f\text {CO}}_{2} = K \cdot (a_{\text {subskin}}\text {fCO}_{2w} - a_{\text {skin}}\text {fCO}_{2a}) \end{aligned}$$
(12)

where a is the solubility of CO2 in seawater (mol kg-1 atm-1), calculated by Weiss [10]:

$$\begin{aligned} \begin{aligned} \ln a\ = - 60.2409 + 93.4517\left( \frac{100}{T_{\text {subskin}}} \right) \ 23.3585 \times \ln \left( \frac{T_{\text {subskin}}}{100} \right) \ S \\ \times \left[0.023517 - 0.023656 \times \left( \frac{T_{\text {subskin}}}{100} \right) + 0.0047036 \times \left( \frac{T_{\text {subskin}}}{100} \right) ^{2}\ \right]\end{aligned} \end{aligned}$$
(13)

In Equation 12, asubskin is calculated by the subskin temperature, askin is calculated by the skin temperature. \(\text {fCO}_{2w}\) is the fugacity of subskin seawater CO2, \(\text {fCO}_{2w}\) is the fugacity of subskin seawater CO2, \(\text {fCO}_{2a}\ \)is the fugacity of atmospheric CO2, and K is the exchange rate, which is usually considered as a function of wind speed .

$$\begin{aligned} K = \Gamma {(660/\text {Sc})}^{0.5}U^{2} \end{aligned}$$
(14)

Here, Sc is the Schmidt number of CO2 in seawater at a given \(T_{\text {subskin}}\) temperature, such that:

$$\begin{aligned} Sc = \ 2073.1 - 125.62 \times T_{\text {subskin}} + 3.6276 \times T_{\text {subskin}}^{2} - 0.043219 \times T_{\text {subskin}}^{3} \end{aligned}$$
(15)

where U is the monthly mean wind speed (m/s) at 10 m height from the cross-calibrated multi-platform ocean surface wind vector analysis product and \(\Gamma \) is the scale factor which was evaluated based on different wind speed products (e.g., 0.39, 0.251, 0.31, etc.) and have been used in other studies [14, 24, 28]. Based on an average wind speed of 6.38 m s–1 in the ECMWF product the scale factor of 0.31 was used to reach a global mean transfer velocity of 16 cm h–1, consistent with the new radiocarbon-based constraints.

2.4 Evaluation

Due to the limited observation data in the Southern Ocean, the data set used for verification will be very small, so the segmentation of the data set will lead to huge differences between RMSE and mean absolute error. In order to ensure reliable model verification, we used 100% data to train, test and verify the model, and continuously optimized the neural network model and the internal weight. Finally, the neural network was used to predict the observed area. RMSE is calculated to be 8.86 \(\mu \)atm, while MAE is 5.01.

Fig. 5
figure 5

Scatter fit of product data and observation data with same station

Full size image

Figure 5 shows that the predicted values are very close to the observed values and R2= 0.93. In Table 1, we list the RMSE and MAE between the results of different algorithms and the actual values. SOM-FFNN merged a self-organizing map (SOM) and feedforward neural network, and the RMSE is 12.24. LSCE-FFNN employed the Laboratory of Climate and Environmental Sciences, and the RMSE is 17.40. We conclude that the CA-FFNN-based models outperform both the SOM–FFNN and LSCE–FFNN.

Table 1 Comparison of our Algorithms’ Errors to LSCE-FFNN and SOM-FFNN
Full size table

3 Results and Discussion

3.1 Seasonal Variation in Southern Ocean Sea Surface pCO2

According to the new dataset, the pCO2 data changes periodically with the seasons. This result is consistent with the seasonal changes in other studies [16, 25, 27]. The seasonal mean amplitude of ocean surface pCO2 in the southern ocean was 13.02 \(\mu \)atm and our data has similar seasonal variation characteristics compared with the observational data of the Southern Ocean [15], the pCO2 reaching its minimum in summer, and increase in winter (Fig. 6), and driven by both biological and physical factors, pCO2 in the Southern Ocean shows obvious seasonal changes [22], In winter, due to the enhancement of the wind field in the Southern Ocean, as shown in the Fig. 7, the Ekman transport caused by the wind field also intensifies [1, 7], strengthening upwelling and improving the efficiency of the biological pump.

Fig. 6
figure 6

In SOFS, the product data and real value

Full size image
Fig. 7
figure 7

From 1998 to 2018, the normalized mean monthly U-component of wind and pCO2 was calculated

Full size image
Fig. 8
figure 8

From 1998 to 2018, the average monthly CHL and pCO2 data were normalized

Full size image

The dissolved inorganic carbon in the bottom layer migrates to the surface layer under the influence of the upwelling, making the surface pCO2 increase continuously. With the melting of sea ice in the Southern Ocean in summer, marine primary productivity gradually recovers, the Chl-a concentration increases, as shown in Fig. 8, and CO2 in sea water is absorbed through photosynthesis [26], which lead to surface pCO2 decrease. This period is mainly due to biological factors.

Fig. 9
figure 9

a is monthly fluctuations in the Southern Ocean’s pCO2 (atm) from 1998 to 2018; b is yearly fluctuations in the Southern Ocean’s pCO2 (atm) from 1998 to 2018

Full size image

3.2 Annual Variation in Southern Ocean Sea Surface pCO2

Analyzing the inter-annual change of the reconstructed pCO2 data from 1998 to 2018, the mean surface pCO2 of the Southern Ocean increased from 351.88 \(\mu \)atm to 372.65 \(\mu \)atm—a total increase of 20.77 \(\mu \)atm in 21 years and an annual mean increase of 0.99 \(\mu \)atm/yr. As shown in Fig. 9, the Southern Ocean pCO2 has maintained a high growth rate.

By calculating the linear rate of change in the Southern Ocean spatial region over a 21-year period, it is found that the pCO2 in most areas is gradually increasing, as shown in Fig. 10. The growth rate around \(35\,^{\circ }\)to \(55\,^{\circ }\) is faster than other regions. Since 2002, many study results have shown that pCO2 in the Southern Ocean has maintained a high growth rate [23], and our data also shows this trend.

Fig. 10
figure 10

The rate of change in the surface Southern Ocean’s pCO2 (\(\mu \)atm yr-1) concentration

Full size image

3.3 Variability in Sea—AirCO2 Flux

As for the rate of change of \(\Delta \)f\(CO_2\), Most of the Southern Ocean is transforming into a carbon sink area. The black/red dots in Fig. 11 represent \(\Delta \)f\(CO_2\) regions toward positive/negative trends with high change rate. According to the distribution of pCO2 in the Southern Ocean since 1998, the status of inner ring (\(50-70\,^{\circ }\)S) as a carbon source is changing, while the outer ring (\(35-50\,^{\circ }\)S) has always maintained a strong carbon sink state, and there is no tendency to weaken. The changes of CO2 flux in the Southern Ocean calculated by our model are consistency with other models for the evolution of intensity [19]. Using Eq. 12 to calculate the CO2 flux, the Southern Ocean’s CO2 flux was found to have changed substantially over the past two decades. The \(\Delta \)f\(CO_2\) in the Southern Ocean also changes regularly with the seasons, with the strongest in early summer and get the weakest at the end of winter (Fig. 13). Many studies have shown that in early 1990s, the Southern Ocean was saturated with carbon and regained its vitality at the beginning of the 21st century [4]. The data products reproduces the strong increase of carbon sinks in the Southern Ocean since the 21st century (Fig. 14).

Fig. 11
figure 11

Carbon sink when \(\Delta \)f\(CO_2<0\), carbon source when \(\Delta \)f\(CO_2\)>0, Rate of change in the \(\Delta \)f \(CO_2\) of the Southern Ocean

Full size image
Fig. 12
figure 12

\(CO_2\) flux trends in of the Southern Ocean from 1998 to 2018

Full size image
Fig. 13
figure 13

Changes in \(\Delta \)f\(CO_2\) values by month and year from 1998 to 2018 (\(\mu \)atm). The gray lines indicate fluctuations in previous years, whereas the colorful lines represent variations in the year under consideration

Full size image
Fig. 14
figure 14

Each month’s average \(CO_2\) flux in \(50-70\,^{\circ }\)S (Pg C). The Southern Ocean was a carbon supply in the red columns, whereas the Southern Ocean was a carbon sink in the black columns

Full size image

In terms of interannual changes, the carbon sink of the Southern Ocean increased from -0.21 Pg C yr-1 in 1998 to -1.67 Pg C yr-1 in 2018.

One standard deviation was used as an indicator of error:

$$\begin{aligned} \sigma _{n} = \sqrt{\frac{\sum _{i = 1}^{n}\left( x_{i} - \overline{x} \right) ^{2}}{n^{2}}} \end{aligned}$$
(16)

where \(x_{i}\) is the actual value, \(\overline{x}\) is the mean value of x, n is number of data, and the error range was within ± 0.0.087 Pg C yr-1.

We found that the carbon sinks in the Southern Ocean did not always maintain a trend of rapid growth. During 2010-2013, the carbon sinks stagnated. As shown in Fig. 12, we found the similar phenomenon in many other reconstructed data [5].Many studies have shown that changes in the Southern Annular Mode (SAM) led to the stagnation of carbon sinks in the 1990s [5]. However, the stagnation was not strongly correlated with the SAM. Stability during this period was mainly due to the weakening of the carbon sink intensity from \(35-50\,^{\circ }\)S.Changes in this region have also been attributed to the barometric asymmetry of the Zontal Waves 3 (ZW3) model [9]. As for models that rely on observational data, it is difficult to capture such large and subtle inter-annual changes.

As shown in Fig. 16, there is an obvious double-ring structure before 2010, which is not always a carbon sink. The inner ring (\(50-70\,^{\circ }\)S), change with the seasons. In April, May, June, July, August, and September, the region serves as a carbon source, emitting CO2 into the atmosphere. In October, November, December, January, February, and March, it absorbs CO2, as shown in Fig. . The outer ring (\(35-50\,^{\circ }\)S) is the main carbon sink region (Fig. 15), and undertakes most CO2 absorption. From the perspective of the inter-annual changes in the entire region, the Southern Ocean carbon dioxide flux changes to carbon sinks.

Fig. 15
figure 15

Each month’s average CO2 flux in \(35-50\,^{\circ }\)S (Pg C). The Southern Ocean was a carbon sink, as indicated by the blue columns

Full size image
Fig. 16
figure 16

In the Southern Ocean, mean sea surface \(CO_2\) fluxes (Pg C) were measured in 1998, 2003, 2006, 2010, 2014, and 2018

Full size image

However, with the increase of carbon sink in the outer ring and the weakening of the carbon source in the inner ring, after 2010 this ring structure is gradually disappearing. As shown in Fig. 16, most Southern Ocean regions become carbon sinking regions, because the \(\Delta \)f\(CO_2\) in the Southern Ocean decrease significantly since 1998.

4 Conclusion

In this chapter, we propose a feedforward neural network for reconstructing pCO2 data in the Southern Ocean that is generalizable for reconstructing regional data. The reconstruction process consists of two steps. First, we collect all parameters that may have impact on pCO2 from the literature and experimental data and obtain the covariance matrix of the variables by calculation. The parameters with higher correlation coefficient values and an effect on the process change of pCO2 were kept as inputs FFNN, and the final model was constructed and used to reconstruct the pCO2 data of the Southern Ocean with a monthly temporal resolution and a spatial resolution of \(1\,^{\circ }\times 1\,^{\circ }\) in the second step after continuous and iterative calculation and optimization.

First of all, we find the key parameters that affect pCO2 in the Southern Ocean changes. Secondly, use the advantages of neural network technology to interpolate in the data sparse area, and build a new model by filtering parameters. Finally, in the Southern Ocean, we compare the new data with the measured data and get the root mean square error with 8.86 \(\mu \)atm which is better than the data reconstructed from global data.

The results of our reconstruction demonstrate that pCO2 in the Southern Ocean’s surface layer varies seasonally and has risen since 2000. It did, however, reach a halt from 2010 and 2013, after which it resumed its upward trend. In the Southern Ocean, carbon dioxide flux is distributed in a double ring shape. The primary carbon sink region is \(35-50\,^{\circ }\)S; south of \(50\,^{\circ }\)S, seasonal carbon sources and sinks alternated. Despite the fact that our findings are consistent with earlier studies, the reconstructed surface pCO2 products require ongoing verification. Our model will improve as the frequency and range of observations in the Southern Ocean increase.