Keywords

1 Introduction

Frame structures are widely used in multi-story buildings, high-rise buildings and stadiums. Due to the multiple influencing factors, such as long-term effect of loads, environmental corrosion, aging of structural materials, earthquake action, and typhoon action, etc., the accumulative damage will occur in frame structures within their service period, even worse, may lead to engineering accidents. Therefore, it is necessary to study the problem of damage identification of frame structures. Vibration-based structural damage identification method is one of the effective ways to solve this problem. The basic principle of this method is as follows: As the structural damage appears, the physical parameters of the structure change [1,2,3,4,5]. Therefore, combining certain identification techniques, it is possible to identify structural damage by using the measured responses or the indexes indirectly calculated from the measured responses, such as natural vibration frequencies [6], modal shapes [7], modal curvatures [8], residual forces [9], flexibility matrix [10, 11], modal strain energy [12], etc.

In the past three decades, several notable achievements had been made in the research of vibration-based damage identification methods of frame structures. The damage identification of the superstructural members (such as beams and columns or joints) of two-dimensional plane frame structures was firstly studied by adopting vibration-based damage identification methods. These research works were mainly based on the measured responses or the indexes indirectly calculated from the measured responses, such as strain modal shapes [13], modal frequencies and displacement modal shapes [14,15,16,17,18,19,20,21], modal strain energy [22], the measured displacement responses [23, 24], the measured acceleration responses [25,26,27]. In these works, some can only effectively identify the damage location of the superstructure members of two-dimensional plane frame structures [13, 14, 16, 23, 26], while others can effectively identify the damage location and damage degree both [15, 17,18,19,20,21,22, 24, 25, 27]. The above research works showed that the vibration-based damage identification methods can identify the damage of the superstructural members of two-dimensional plane frame structures. However, the actual frame structures are relatively complex three-dimensional spatial structures. The effectiveness of the vibration-based damage identification methods for the damage identification of three-dimensional frame structures needs further verification. Therefore, the damage identification of the superstructural members of three-dimensional frame structures was further studied by adopting vibration-based damage identification methods. These research works were also mainly based on the measured responses or the indexes indirectly calculated from the measured responses, such as modal frequencies and modal shapes [28,29,30,31,32,33], modal strain energy [34], the measured displacement responses [35], the measured acceleration responses [36,37,38]. In these works, some can only effectively identify the damage location of the superstructure members of three-dimensional plane frame structures [32, 34, 36, 38], while others can effectively identify the damage location and damage degree both [28,29,30,31, 33, 35, 37]. The above research works showed that the vibration-based damage identification methods can identify the damage of the superstructural members of three-dimensional plane frame structures. It seems that the above research can solve the problem of damage identification of actual frame structures. However, the existing research works on vibration-based damage identification methods of frame structures mainly focused on the damage identification of beams and columns or joints of frame structures, but the damage identification of floor slabs in frame structures has not been considered. At the same time, the existing methods are proposed under the rigid base assumptions, without considering the influences of the soil-foundation-structure interaction (SSI) effect. However, the SSI effect will make the dynamic characteristics and responses of the structural system great differences with the rigid foundation assumption situation. It will inevitably affect the accuracy of the vibration-based damage identification methods. In addition, the existing methods for damage identification of frame structures are merely applicable to the damage identification of its superstructural members, but not applicable to the damage identification of its hidden substructural members. Therefore, it is necessary to study the damage identification method of soil-foundations-frame structure as a whole, so as to realize the joint identification of superstructural and substructural damage. As the authors’ knowledge, there has been no research on this issue.

In this paper, a vibration-based method to jointly identify the damage locations of the superstructure and substructure of the piles-supported frame structures was proposed. Firstly, the high-efficiency modes which are sensitive to the damage of the piles-supported frame structure were determined. Then, the element modal strain energy difference functions of the high-efficiency modes were calculated before and after the damage, and finally the damage locations were identified by the average values of the absolute values of the wavelet transform coefficients of the element modal strain energy difference functions of high-efficiency modes. Through numerical simulation, the feasibility of the proposed vibration-based method to jointly identify the damage locations of the superstructure and substructure of the piles-supported frame structures was preliminarily verified.

2 The Description of the Proposed Damage Identification Method

In this paper, the proposed damage identification method for piles-supported frame structure is introduced from the following aspects: damage identification process, high-efficiency modes determination, element modal strain energy and strain energy difference functions calculation, wavelet transform analysis, and damage identification index.

2.1 Damage Identification Process

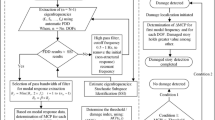
The identification process of the proposed damage identification method is shown in Fig. 1. Specific identification steps are illustrated as follows:

Fig. 1.
figure 1

Flow chart of damage identification of piles-supported frame structure.

Full size image

Firstly, the finite element model of undamaged piles-supported frame structure will be established based on the available engineering data. Through the modal analysis, the modal frequencies and modal shapes of undamaged piles-supported frame structure will be obtained.

Secondly, by means of environmental excitation, the vibration response data of the damaged piles-supported frame structure will be obtained under the operating state. Through the modal identification, the measured modal frequencies and modal shapes of the damaged piles-supported frame structure will be obtained.

Thirdly, the high-efficiency modes will be determined by calculating the change rate of modal frequency of each order mode of the piles-supported frame structure before and after damage.

Fourthly, the element modal strain energy of the corresponding high-efficiency modes of the undamaged and damaged piles-supported frame structure will be calculated respectively. Then, the difference functions of element modal strain energy of the high-efficiency modes will be calculated before and after the damage.

Finally, the damage locations of corresponding members (such as beams, columns, plates and piles) can be determined by the average values of the absolute values of the wavelet transform coefficients obtained from wavelet transform analysis of the difference functions of element modal strain energy of the high-efficiency modes.

2.2 High-Efficiency Modes Determinations

According to the change rate \(\delta\) of modal frequency of each mode before and after damage, the high-efficiency modes used for structural damage identification will be selected. The change rate \(\delta_i\) of modal frequencies of the ith mode before and after damage can be calculated by Eq. (1).

$$\delta_i = \frac{{f_i^{\text{u}} - f_i^{\text{d}} }}{{f_i^{\text{u}} }} \times {100}\%$$
(1)

Where \(f_i^{\text{u}}\) and \(f_i^{\text{d}}\) are the modal frequencies of the structure’s ith mode before and after damage, respectively, in Hz.

The existence of structural damage can be judged according to \(\delta_i\). The larger the \(\delta_i\) value is, the mode is more sensitive to the structural damage.

The high-efficiency modes for subsequent damage identification will be selected according to the following criteria: Firstly, the mode which has the largest \(\delta\) value will be selected. Secondly, the modes that their \(\delta\) values are not less than 80% of the largest \(\delta\) value will be selected. If the number of selected modes is only one order, the selection criteria can be appropriately relaxed to ensure the number of the selected modes is not less than two orders.

2.3 Element Modal Strain Energy and Strain Energy Difference Functions Calculation

The element modal strain energy can be calculated by modal shapes and stiffness matrix. Since the element modal strain energy can reflect the change of local characteristics of the structure and it is sensitive to the local structural damage which is much higher than that of the modal shapes. Therefore, the element modal strain energy will be used as the basic quantity to determine the locations of structural damage.

The element modal strain energy of the ith high-efficiency mode of the jth element can be calculated as follows [39,40,41,42,43,44]:

$$MSE_{i,j}^{\text{u}} = ({\bf{\Phi }}_\iota^\upsilon )^{\text{T}} {\bf{K}}_j^{\text{u}} {\bf{\Phi }}_i^{\text{u}}$$
(2)
$$MSE_{i,j}^{\text{d}} = ({\bf{\Phi }}_i^{\text{d}} )^{\text{T}} {\bf{K}}_j^{\text{d}} {\bf{\Phi }}_i^{\text{d}}$$
(3)

Where \(MSE_{i,j}^{\text{u}}\) and \(MSE_{i,j}^{\text{d}}\) are the element modal strain energy of the ith high-efficiency mode of the jth element before and after damage respectively; \({\bf{K}}_j^{\text{u}}\) is the element stiffness matrix of the jth element before damage; \({\bf{K}}_j^{\text{d}}\) is the element stiffness matrix of the jth element after damage. Since the element stiffness after damage cannot be measured, \({\bf{K}}_j^{\text{u}}\) is generally adopted to replace \({\bf{K}}_j^{\text{d}}\).

The difference function of the element modal strain energy of the ith high-efficiency mode of the jth element before and after damage,\(MSEC_{i,j}\), can be obtained by Eq. (4).

$$MSEC_{i,j} = MSE_{i,j}^{\text{u}} - MSE_{i,j}^{\text{d}}$$
(4)

2.4 Wavelet Transform Analysis

Once the structure is damaged, the \(MSEC\) value of the element which located in the structure damage area will be small obvious change. Due to the wavelet transform can analyze the change of signal data well [23]. Therefore, in order to obtain better identification effect of damage localization, the one-dimensional continuous wavelet transform (CWT) will be used to analyze the \(MSEC\) value of the element of each high-efficiency mode. The biorthogonal spline wavelet function bior6.8 will be used as the wavelet basis function. The sequence constituted by \(MSEC_{i,j}\) values will be taken as the real-valued input signal, and the element number which is corresponding to location of the element will be taken as the time variable. The absolute values of the wavelet transform coefficient of the element modal strain energy difference function of the ith high-efficiency mode of the jth element, \(MSECD_{i,j}\), will be obtained by wavelet transform. According to the peak of \(MSECD_{i,j}\) values with the number of elements, the locations of the structure damage can be determined.

2.5 Damage Identification Index

In order to reduce the influence of random noise, the n order high-efficiency modes will be used to identify damage locations of the structure. The average value of the absolute values of the wavelet transform coefficients of the element modal strain energy difference functions of high-efficiency modes, MSECM, will be used as the damage identification index. The average value of the absolute values of the wavelet transform coefficients of the element modal strain energy difference functions of high-efficiency modes of the jth element, \(MSECM_j\), can be calculated by Eq. (5). The damage locations of the structure will be identified according to the peak of the above damage identification index along with the locations of the elements.

$$MSECM_j = \frac{1}{n}\sum_{i = 1}^n {MSECD_{i,j} }$$
(5)

3 Damage Identification Numerical Simulation

3.1 Numerical Modeling of Piles-Supported Frame Structure Test Model

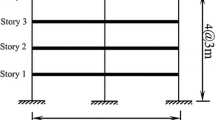
The numerical simulation study had taken the test model (as show in Fig. 2 and Fig. 3) of the subsequent model test as the simulation object. The model test has not been carried out yet, and the feasibility of the proposed method was preliminarily discussed in this paper based on the numerical simulation.

The finite element models of undamaged and damaged cases of the piles-supported frame structure test model were established.

The integral finite element model of soil-piles-frame structure under undamaged case was established by using ANSYS software, as shown in Fig. 4. The finite element model of piles-frame structure is shown in Fig. 5 (soil, soil box and concrete base are not shown).

Fig. 2.
figure 2

The design of test model (unit: mm). (a) Front elevation. (b) Side elevation. (c) Section. (d) Layout of measuring points.

Full size image
Fig. 3.
figure 3

The design of test soil box and the layout of the test model (unit: mm). (a) Layout of test model in the soil box. (b) Section 1–1.

Full size image
Fig. 4.
figure 4

The finite element model of the undamaged soil-piles-frame structure system.

Full size image
Fig. 5.
figure 5

The finite element model of piles-frame structure system.

Full size image

The corresponding dimensions of beams, columns, piles, floor slabs, cap, soil field, soil box and concrete base are same as the test model, as shown in Fig. 2 and Fig. 3.

In the numerical simulation study, the assumed values of material parameters are as follows: The elastic modulus, density and Poisson ratio of steel are 2.1 × 105 MPa, 7850 kg/m3 and 0.33, respectively. The elastic modulus, density and Poisson ratio of loose sand are 25 MPa, 1900 kg/m3 and 0.35, respectively. The elastic modulus, density and Poisson ratio of dense sand are 120 MPa, 2000 kg/m3 and 0.3, respectively. The elastic modulus, density and Poisson ratio of Polystyrene foam plate are 7 MPa, 30 kg/m3 and 0.3, respectively. The elastic modulus, density and Poisson ratio of concrete are 3 × 104 MPa, 2500 kg/m3 and 0.2, respectively.

The steel beams, steel columns and steel pipe piles were simulated by beam188 elements. The steel floor slabs and soil box were simulated by shell63 elements. The steel cap, soil, Polystyrene foam plate and concrete base were simulated by solid45 solid elements. Each steel beam, steel column and steel pipe pile was all divided into 10 elements. Each steel floor slabs was divided into 144 elements. Steel soil box was divided into 1520 elements. The steel cap, soil, Polystyrene foam plate and concrete base were divided into 36 elements, 4680 elements, 920 elements and 1536 elements respectively.

At the bottom of the concrete base, the solid boundary was adopted. As the structural responses under environmental excitation are generally small, the nonlinear effects of soil and the separation and slip between piles and soil have no obvious influence on the structural responses. Therefore, the nonlinear effects mentioned above were ignored in the numerical simulation.

3.2 Damage Identification Numerical Simulation Cases

The damage cases of the numerical simulation study are shown in Table 1. The damage location numbers are shown in Fig. 5, where ① represents the damage of pile top element, ② represents the damage of the element at the top of the first layer of the column, ③ represents the damage of the element at the end of the second floor side beam, and ④ represents the damage of the element at the mid-span of the third floor slab. In the numerical simulation, the stiffness of the corresponding damage element was reduced to simulate the damage of the structure. For each damage cases, only by modifying the material parameters at the corresponding damaged element (reducing the elastic modulus) on the basis of the undamaged piles-supported frame structure finite element model, the damaged structure finite element model under the corresponding damage cases were obtained.

Table 1. Damage identification numerical simulation cases
Full size table

3.3 Modal Analysis and High-Efficiency Modes Selection

The modal shapes calculated from the above six damaged cases models are similar to the undamaged case model, with the mode numbers corresponding to each other. Figure 6 shows the modal frequency change rates of the first 50 modes in each damaged case. According the Fig. 6 and the selection criteria of high-efficiency mode described in Sect. 2.2, the high-efficiency modes can be determined for each damaged case, as shown in the Table 2.

The high-efficiency modes determined in Table 2 are shown in Fig. 7 (soil, soil box and concrete base are not shown). The modal frequencies of the modes corresponding to Fig. 7 calculated from the models of the undamaged and damaged cases are shown in Table 3.

Fig. 6.
figure 6

The frequency change rate \(\delta_i\) of the first 50 modes for damaged. (a) Case 1. (b) Case 2. (c) Case 3. (d) Case 4. (e) Case 5. (f) Case 6.

Full size image
Table 2. Selection of high-efficiency modes for damaged cases
Full size table
Fig. 7.
figure 7

The modal shapes of high-efficiency modes. (a) 1-order. (b) 2-order. (c) 3-order. (d) 5-order. (e) 13-order.

Full size image
Table 3. The modal frequencies of the high-efficiency modes of undamaged and damaged models (unit: Hz)
Full size table

4 Results and Analysis of the Damage Identification Numerical Simulation

4.1 Results and Analysis of the Single Damage Identification

In order to verify the validity of the proposed method in this paper for damage location identification of a single damaged case, the damage identification algorithm mentioned above was used to identify the damage locations of damaged cases 1 to 4. Figure 8, Fig. 9, Fig. 10 and Fig. 11 show the damage location identification results of the above four damaged cases.

Figure 8 shows that the damage identification results for damaged case 1. The average values of the absolute values of the wavelet transform coefficients of the element modal strain energy difference functions of high-efficiency modes (namely MSECM values) of pile element No. 9375 and its adjacent pile element No. 9376 have an obvious peak. The MSECM values of column elements, beam elements and slab elements change small. Furthermore, the MSECM value of the pile element No. 9375 is the largest of all. Therefore, it is known that there may be damage at and near pile element No. 9375.

Fig. 8.
figure 8

The damage identification results of the damaged case 1. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image

Figure 9 shows that the damage identification results for damaged case 2. The MSECM values of column element No. 30 and its adjacent column element No. 29 and beam elements No. 563, 572 to 573 and 582 have an obvious peak. The MSECM values of pile elements and slab elements change small. Furthermore, the MSECM value of the column element No. 30 is the largest of all. Therefore, it is known that there may be damage at and near column element No. 30.

Fig. 9.
figure 9

The damage identification results of the damaged case 2. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image

Figure 10 shows that the damage identification results for damaged case 3. The MSECM values of beam element No. 623 and its adjacent beam element No. 624, slab elements No. 385 to 387 and 406 to 408, column elements No. 61, 70, 101 and 110 have an obvious peak. The MSECM values of pile elements change small. Furthermore, the MSECM value of the beam element No. 623 is the largest of all. Therefore, it is known that there may be damage at and near beam element No. 623.

Fig. 10.
figure 10

The damage identification results of the damaged case 3. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image

Figure 11 shows that the damage identification results for damaged case 4. The MSECM values of slab element No. 475 and its adjacent slab elements No. 474 to 476 have an obvious peak. The MSECM values of pile elements, column elements and beam elements change small. Therefore, it is known that there may be damage at and near slab element No. 475.

Fig. 11.
figure 11

The damage identification results of the damaged case 4. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image

Through the numerical simulation results of the above four single damaged cases, it can be seen that the proposed damage location identification method in this paper can better identify the damage location of single damage that may exist in different parts of the piles-supported frame structure. Despite the influence of adjacent effect exists, but the damage area of the piles-supported frame structure still can be effectively located.

4.2 Results and Analysis of the Multiple Damage Identification

In order to verify the validity of the proposed method in this paper for damage location identification of a multiple damaged case, the damage identification algorithm mentioned above was used to identify the damage locations of damaged cases 5 to 6. Figure 12 and Fig. 13 show the damage locations identification results of the above two damaged cases.

Figure 12 shows that the damage identification results for damaged case 5. There are two main locations where the MSECM values have an obvious peak: (1) Pile element No. 9375 and its adjacent pile element No. 9376. (2) Column element No. 30 and its adjacent beam elements No. 563, 572 to 573 and 582. The MSECM values of slab elements change small. Furthermore, the MSECM value of the pile element No. 9375 is the largest in the pile elements. The MSECM value of the column element No. 30 is the largest in the column elements. Therefore, it is known that there may be damage at and near pile element No. 9375 and column element No. 30.

Figure 13 shows that the damage identification results for damaged case 6. There are two main locations where the MSECM values have an obvious peak: (1) Pile element No. 9375 and its adjacent pile element No. 9376. (2) Beam element No. 623 and its adjacent beam element No. 624, slab elements No. 385 to 387 and 406 to 408 and column elements No. 61, 70, 101 and 110. Furthermore, the MSECM value of the pile element No. 9375 is the largest in the pile elements. The MSECM value of the beam element No. 623 is the largest in the beam elements. Therefore, it is known that there may be damage at and near pile element No. 9375 and beam element No. 623.

Fig. 12.
figure 12

The damage identification results of the damaged case 5. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image
Fig. 13.
figure 13

The damage identification results of the damaged case 6. (a) Pile elements. (b) Column elements. (c) Beam elements. (d) Slab elements.

Full size image

Through the numerical simulation results of the above two multiple damaged cases, it can be seen that the proposed damage location identification method in this paper can better identify the damage locations of multiple damage that may exist in different parts of the piles-supported frame structure. Despite the influence of adjacent effect exists, but the damage areas of the piles-supported frame structure still can be effectively located.

5 Conclusion and the Prospect of Further Research

A vibration-based damage identification method for the damage location jointly identification of superstructure and substructure of the piles-supported frame structure was proposed, which takes the soil-piles-frame structure as a whole for damage identification. The influence of soil-piles- structure interaction on the damage identification of piles-supported frame structure was considered. The validity of the proposed method was preliminarily verified by numerical simulation. The results show that the method can identify the damage location of the piles-supported frame structure under the cases of single damage or multiple damage, and can effectively locate the damage area in spite of the adjacent effect exist. In addition, the damage locations of hidden pile foundation can be identified by this method.

It should be pointed out that the above research work is a preliminary numerical simulation study under the assumption that the modal parameters of the damaged structure have been obtained and the influence of random noise is not considered. In order to apply this method to damage identification and health monitoring of piles-supported frame structures, the following problems need to be further studied:

Firstly, how to predict the acceleration response data of unknown measurement points of damaged structure based on the acceleration response data of limited known measurement points of damaged structure? This problem can be solved by predicting the acceleration response data of the unknown measurement points of the damaged structure according to acceleration response data of the known measurement points of the damaged structure and the acceleration response transitivity function of the known and unknown measurement points of the undamaged structure.

Secondly, how to identify the modal frequencies and mode shapes of the damaged structure according to the acceleration response data of measuring points (including the acceleration response data of the known measuring points and the predicted acceleration response data of unknown measuring points)? This problem can be solved by using stochastic subspace method to identify the modal frequencies and mode shapes of the damaged structure according to the acceleration response data of the damaged structure.

Thirdly, how to effectively identify the damage degree of damaged structure when the location of structural damage is known? This problem can be solved by using support vector machine (SVM) method to identify the damage degree of damaged structure.

Finally, the further numerical and experimental verification of actual feasibility of damage location and damage degree identification of soil-pile-frame structure should be carried out. Combined with the results of the above three further research work and considering the acceleration response of random noise effects, further numerical simulation and model tests research work will be carried out to verify the effectiveness and robustness of the joint identification method for the damage of superstructure and substructure of piles-supported frame structure.

The vibration-based joint identification method for the damage of superstructure and substructure considering soil-foundation-structure interaction is a challenging work, which can further improve the structural health monitoring research work of actual engineering. The purpose of this research report in this paper also hopes to attract more relevant researchers to adopt more effective methods and means to study this problem.