Investigating the Self-Efficacy Beliefs and Classroom Practices of Out-of-Field, In-Field, and Upskilled Mathematics Teachers

Abstract

The study that we report in this chapter contributes to our broader research agenda for evaluating the impact of a national professional development programme that upskills out-of-field post-primary mathematics teachers in Ireland. The aim of the study was to compare the self-efficacy beliefs, perceived and observed classroom practices of six post-primary mathematics teachers (three groups of 2) who were either out-of-field, upskilled via the professional development programme, or in-field. The teachers completed surveys of their self-efficacy beliefs and approaches to teaching mathematics. Video recordings of three mathematics lessons taught by each teacher were analysed using the Productive Pedagogies classroom observation framework. The findings showed that there were similarities and differences between the three groups of teachers; however, the upskilled teachers were developing self-efficacy beliefs and pedagogical practices that are similar to those of in-field teachers of mathematics.

1 Introduction

‘Out-of-field’ teaching is an international phenomenon that involves teachers being assigned to teach subjects that do not match their training or education (Ingersoll, 2002). This practice seems particularly prevalent in mathematics. Out-of-field teachers of mathematics generally possess a teaching qualification that is not mathematics-specific, and so they typically lack the necessary mathematics content knowledge and pedagogical content knowledge that are required for developing students’ mathematical understanding (Baumert et al., 2010). Out-of-field teachers may also have low confidence levels, especially in relation to the subject content they are teaching, and this can impact their classroom practice and hinder their development of a professional identity in their out-of-field subject (Du Plessis, 2016).

There is growing recognition of the need for professional development programmes that meet the needs of out-of-field teachers (Du Plessis et al., 2015). While programmes are being developed in some countries, little research has so far been conducted on their effectiveness (Faulkner et al., 2019). In addition, there have been calls for research into the teaching practices of out-of-field teachers (Ní Ríordáin et al., 2017). This chapter aims to address these identified research gaps. We report on aspects of a larger study that is evaluating the impact of a long-term, large-scale, government-funded, nationally consistent and university-accredited programme offered to out-of-field teachers of mathematics in Ireland—the Professional Diploma in Mathematics for Teaching (PDMT).

2 Background and Context

In Ireland, growing concerns about the underperformance of post-primary school students in mathematics at the beginning of the twenty-first century, coupled with the low uptake of Higher Level mathematics in the senior post-primary years, led to an overhaul of the post-primary school mathematics curriculum. This new curriculum, known locally as ‘Project Maths’, was introduced in 2010 and shifted the emphasis away from memorisation and procedures towards understanding and problem-solving (National Council for Curriculum & Assessment, 2005). A national survey of mathematics teachers, conducted by Ní Ríordáin and Hannigan (2009) around the same time as the introduction of Project Maths, revealed that 48% of respondents were teaching mathematics without recognised subject-specific qualifications. Such a high incidence of out-of-field teaching may be due to the small size of many schools in Ireland and the autonomy accorded to school principals in the recruitment and assignment of teachers to subjects and classes. Ní Ríordáin and Hannigan’s finding was perceived by education policy makers as a potential threat to the successful implementation of the new mathematics curriculum. In response to this survey, the Department of Education and Skills (DES) funded a national programme (PDMT) to develop out-of-field teachers’ content and pedagogical content knowledge in mathematics to meet the required level as specified by the Irish Teaching Council (2013). The Teaching Council requires that in mathematics, fully qualified teachers must have a degree qualification with the specific study of mathematics comprising at least one-third of the degree. There are also minimum credit requirements in algebra, analysis, geometry, and probability and statistics with additional credits to be obtained in a variety of optional topics.

The PDMT is a two-year part-time postgraduate programme with teachers’ tuition fees fully funded by the DES. Delivery of the programme is led by the University of Limerick in conjunction with a national consortium of 13 higher education institutions in Ireland. The PDMT programme comprises ten mathematics modules, each of which is presented over a six-week intensive session, with additional face-to-face and online support. Two year-long mathematics pedagogy modules are delivered face-to-face over weekend workshops and a one-week summer school. The pedagogy modules place an emphasis on classroom practices that foster problem-solving and develop conceptual understanding. One of these pedagogy modules requires participants to complete a supervised action research project on their mathematics classroom practice. Participants of the PDMT programme are usually teaching full-time in schools and are not released from regular duties to undertake the programme. Six cohorts comprising 1078 teachers participated in the PDMT from 2012–2020.

One of the main aims of the PDMT is to develop out-of-field teachers’ knowledge of mathematics content and pedagogy. The programme is also aimed at supporting teachers in developing pedagogical practices that are in alignment with the goals of Project Maths, and this is the focus of the present chapter. We analysed video-recorded mathematics lessons taught by teachers who are currently out-of-field, upskilled (as a result of having completed the PDMT) and in-field, as well as survey responses of these three groups of teachers with respect to their self-efficacy and perceptions of classroom practices. The research question that we investigate is: What insights can be gained from comparing the self-efficacy beliefs, perceived and observed classroom practices of out-of-field, upskilled and in-field teachers of mathematics?

In the following sections, we present a discussion of relevant literature on teacher professional development, self-efficacy beliefs and classroom practices, followed by a summary of our study’s methodology. We then present key findings from analysis of quantitative and qualitative data collected from the teacher participants and reflect on insights into similarities and differences between those who were out-of-field, upskilled and in-field with respect to mathematics.

3 Conceptualising and Evidencing the Impact of Professional Development

Researching the impact of teacher professional development poses methodological and conceptual challenges. Desimone (2009) discussed the strengths, weaknesses and trade-offs between observations, interviews and surveys as the most common methods for studying teacher learning and emphasised the importance of choosing data collection methods to align with research questions. Adler and colleagues (2005) also point out that due to having a personal investment in teaching, it is difficult for teacher educators to take a critical stance towards the research we do with teachers. They suggest the development of strong theoretical languages in order to distance ourselves from what we are looking at. In the present study, as we have the dual roles of researchers and teacher educators in the PDMT, we aimed to achieve this critical distance by situating our research within Desimone’s conceptual framework for studying teacher professional development.

Desimone’s (2009) framework consists of two components. The first component classifies the critical features that define effective professional development in terms of increasing teacher knowledge and skills and improving practice. Drawing on existing empirical research, Desimone proposed that this set of critical features places emphasis on (a) content focus (b) active learning (c) coherence (d) duration and (e) collective participation. The second component of the conceptual framework is ‘an operational theory of how professional development works to influence teacher and student outcomes’ (p. 184). For this component, Desimone proposed a model with the following steps:

• 1. Teachers experience effective professional development (defined in terms of the set of critical features outlined above).

• 2. The professional development increases teachers’ knowledge and skills and/or changes their attitudes and beliefs.

• 3. Teachers use their new knowledge and skills, attitudes and beliefs to improve the content of their instruction or their approach to pedagogy, or both.

• 4. The instructional changes foster increased student learning. (p. 184)

Desimone (2009) acknowledged that other potentially important factors existed, but these were not incorporated into her model because they have not yet been the subject of much research on the impact of professional development. These factors may include, for example, professional identity (Hobbs, 2012), the role of the principal in providing opportunities for teacher learning (Du Plessis et al., 2015), and the role of curriculum materials and implementation (Remillard & Heck, 2014). Desimone also conceded that her model could be criticised as representing a positivist viewpoint. However, she maintained that the model could still be used in studies with different theoretical perspectives on teacher learning as a means of integrating the knowledge generated by empirical research with ‘the emerging consensus of what is good professional development’ (p. 187).

Desimone (2009) noted that it is rare for a single study to investigate all four elements of her proposed model; in particular, there are significant methodological difficulties in designing evaluations that measure the effects of professional development on student achievement. Research conducted by our larger team has analysed the critical features of the PDMT programme (Step 1 in Desimone’s model; see Goos et al., 2020) and its effect on the teachers who participated in the programme (Steps 2 and 3; see Lane & Ní Ríordáin, 2019; Ní Ríordáin et al., 2017; O’Meara & Faulkner, 2021). In this chapter, we further examine the impact of the PDMT on teachers’ self-efficacy beliefs (Step 2) and their classroom practices (Step 3) as key elements in Desimone’s model of teacher change.

4 Teacher Self-Efficacy Beliefs and Classroom Practice

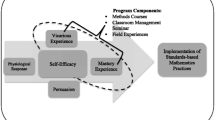
Teacher self-efficacy beliefs refer to the beliefs held by individual teachers about their abilities to perform specific teaching tasks (Dellinger et al., 2008; Enochs et al., 2000). Self-efficacy beliefs are specific to a task and situation, rather than fixed traits of individuals; thus, measures of this construct should assess teacher self-efficacy beliefs in the context in which they are formed (Dellinger et al., 2008). Of relevance to our research on professional development for out-of-field teachers of mathematics is existing evidence that shows teachers with low levels of self-efficacy tend to favour teacher-centred approaches such as reading from a textbook (Czerniak & Schriver, 1994), while highly efficacious teachers are more likely to use student-centred or inquiry approaches (Enochs et al., 2000). Although there has been little research on out-of-field teachers’ self-efficacy beliefs, Ingersoll (1999) proposed that the incorrect assignment of out-of-field teachers to classes and subjects they were not qualified to teach was likely to have a negative impact on their sense of self-efficacy. More recently, O’Meara and Faulkner (2021) surveyed participants in the PDMT to examine their self-efficacy beliefs before and after completing the mathematics pedagogy workshop component of the programme. They found statistically significant improvements in self-efficacy as well as a shift in the teachers’ self-reported classroom practices from teacher-led to student-centred approaches focusing on developing mathematical understanding. This body of research aligns with Desimone’s (2009) conceptual framework, as it suggests that participation in professional development may improve out-of-field teachers’ self-efficacy beliefs and subsequently lead to changes in their classroom practices.

The Productive Pedagogies framework was chosen as the classroom observation instrument for this study as it has been theoretically and statistically validated in Australian research in primary and secondary school classroom across all subject areas (Lingard et al., 2001; Mills et al., 2009). The Productive Pedagogies framework, although not specifically designed for mathematics classrooms, has been used in longitudinal studies of mathematics teaching and is particularly useful for evaluating the intellectual and social environment of the classroom (Maker, 2011). The framework consists of four dimensions. Two of the dimensions, namely Intellectual Quality and Connectedness (shown in the top row of Fig. 15.1), are concerned with the academic outcomes of schooling; the remaining two dimensions of Supportive Classroom Environment and Recognition of Difference are concerned with the social outcomes.

Fig. 15.1

Productive Pedagogies dimensions and components

The Intellectual Quality dimension emphasises the importance of all students being presented with challenging work. Connectedness makes learning meaningful by linking new knowledge to prior knowledge, other subjects in the curriculum, and the world beyond school. In the Supportive Classroom Environment dimension, the focus is on relationships and giving students a voice in the classroom, while Recognition of Difference notes the degree to which students are facilitated to participate as responsible members of a democratic society. A 5-point rating scale is used to provide an index of the variation in quality of classroom practice for each of the twenty components across the four dimensions (Fig. 15.1).

Desimone’s (2009) conceptual framework provides a useful heuristic for studying the impact of teacher professional development. However, it would be an over-simplification to regard the framework as a model of how teachers learn, since it could be interpreted as proposing a linear pathway that does not take account of the complexities of teachers’ professional contexts and histories. Nevertheless, the framework does draw attention to key ‘ingredients’ that need to be considered when seeking to understand teacher change. This is our aim in investigating the possible impacts of the PDMT on teachers’ beliefs about their ability to teach mathematics effectively and their classroom practices as perceived by the teachers themselves and systematically recorded by an independent observer.

5 Methodology

Our research team’s earlier analysis of PDMT participants’ action research reports indicated that teachers perceived a shift over time in their pedagogical practices towards more student-centred approaches that emphasised conceptual understanding and problem-solving (Lane & Ní Ríordáin, 2019). A related study of PDMT participants’ self-efficacy beliefs found statistically significant improvements after completion of the programme’s pedagogy workshops (O’Meara & Faulkner, 2021). A corresponding pre-post research design for investigating the impact of the PDMT on participants’ classroom teaching approaches would require observation of lessons taught before and after the teachers experienced the programme. However, this was not possible due to resource constraints and the demands of delivering a large, complex programme involving 13 higher education institutions. Instead, we designed an instrumental multiple-case study (Stake, 2003) to gain insight into the pedagogical practices of three groups of teachers: (a) those currently teaching mathematics out-of-field (n = 2); (b) those who had been upskilled to fully qualified status by completing the PDMT (n  = 2); and (c) those who had always been fully qualified, in-field teachers of mathematics (n = 2).

The six mathematics teachers participating in the study worked in six different post-primary schools. They were recruited from the 344 teachers who responded to a national survey (adapted from Goos et al., 2019) that examined their perceptions and experiences of teaching mathematics. Those who were interested in participating in a subsequent classroom-based study gave their contact details by completing the final question in the survey. Altogether, 37 of the surveyed teachers indicated initial interest, of whom 30 were in-field, five out-of-field and two upskilled. Upon follow-up, only two of the five out-of-field teachers were willing to participate in this component of the study. It was no surprise to us that teachers were so reluctant to volunteer for research involving classroom observation, since there has been no tradition of teacher observation, peer coaching or mentoring in Ireland (OECD, 2007). Instead, the practice of teaching in Ireland is characterised by ‘pedagogical solitude’ with few opportunities to ‘see, understand and develop pedagogy’ (Conway et al., 2011, p. 90). This culture of professional isolation creates challenges for engaging teachers in classroom-based research.

Selection of the six participants was guided by the replication logic underpinning multiple-case studies, which differs from the sampling logic that applies to surveys (Yin, 2003). Sampling logic requires a statistical procedure to ensure selection of a representative subset of an identified population, whereas cases are instead selected to predict either similar results (literal replication) or contrasting results for predictable reasons (theoretical replication). Both types of replication were built into the design of our study. The participants were six teachers who had contrasting backgrounds in their preparation for mathematics teaching. They comprised the two out-of-field and two upskilled teachers who had indicated willingness to be involved, and two in-field teachers who were selected so as to achieve the best match with the demographic characteristics of the other participants (gender, years of experience of teaching mathematics and teaching assignments in terms of class year level).

The research study was designed to generate rich insights into teacher experience across multiple sites, using both quantitative and qualitative data collection and analysis. The data sources were teacher surveys, pre- and post-lesson interviews and structured classroom observations. To address our research question, only selected survey and observation data are reported in this chapter.

The Teacher PDMT Survey (adapted from an instrument designed by Goos et al., 2019) sought demographic data and included items investigating teachers’ perceptions of their classroom practice. The latter items came from Question 14 in the Trends in International Mathematics and Science Study (TIMSS) Grade 8 Teacher Questionnaire Mathematics (International Association for the Evaluation of Educational Achievement, 2014) and asked respondents to indicate how often they used the listed strategies while teaching their mathematics class: in every/almost every lesson, in about half the lessons, in some lessons or never.

The 31-item Teachers’ Efficacy Beliefs System-Self (TEBS-Self) Survey developed by Dellinger et al. (2008) was also completed by the six teachers. In this chapter, the focus is on three of the survey’s six sub-scales, concerning communicating/clarification, accommodating individual differences and higher order thinking skills. Responses were given on a 4-point scale, indicating whether the teachers’ beliefs in their capabilities were weak, moderate, strong or very strong. All survey data were analysed using the Statistical Package for the Social Sciences (SPSS), with frequencies and means reported where relevant.

Teachers were observed by the second author as they taught six junior secondary mathematics lessons in two blocks of three consecutive lessons. These lessons were also video-recorded for later analysis. In this chapter, we present analyses of three consecutive lessons for each teacher. Before observing and video-recording lessons, the second author discussed the Productive Pedagogies scoring manual with the first author, who is an experienced user of the Productive Pedagogies framework. Both authors used the scoring manual independently to rate an online video of a junior secondary mathematics lesson, after which they compared their ratings and resolved any differences via further discussion. After the data collection was completed, the second author watched the video-recorded lessons, assigned scores for each item and calculated mean scores on each dimension for each of the three types of teachers (out-of-field, upskilled, in-field). Similarities and differences between the teachers were further examined for each dimension by inspecting item scores.

6 Key Findings

6.1 Teacher Demographic Characteristics

Table 15.1 summarises the gender, years of mathematics teaching experience and grouping (out-of-field, upskilled, in-field) of the six participating teachers. The school year in which upskilled and in-field teachers gained their mathematics teaching qualification through the PDMT or initial teacher education programme respectively is also shown in Table 15.1, in addition to the school type (mixed gender, female or male) and class year, mathematics level and class size taught (first-third year; common, foundation, ordinary or higher level mathematics; number of students in class) for each of the six participating teachers.

Table 15.1 Teacher demographic characteristics

6.2 Teacher Self-Efficacy Beliefs

Responses of the six teachers to the relevant items of the Teacher Efficacy Beliefs Survey are recorded in Table 15.2. Looking across the rows of Table 15.2 enables comparison between the three groups of teachers on each self-efficacy item. In general, for each item, the strength of the teacher’s belief in their capabilities increases from out-of-field to upskilled to in-field teachers. The upskilled and in-field teachers reported either strong or very strong beliefs in their capabilities to perform every teaching task listed in the survey: these two groups did not differ greatly in their self-efficacy beliefs. On the other hand, the out-of-field teachers reported only weak or moderate beliefs in their capabilities for most survey items, with one of these teachers indicating stronger self-efficacy beliefs for some items.

Table 15.2 Teacher self-efficacy beliefs

Differences in self-efficacy beliefs of the three groups of teachers were most pronounced for the following three items (shaded in Table 15.2), referring to the teachers’ beliefs in their capabilities to:

• actively involve students in developing concepts;

• actively involve students in critical thinking and/or problem-solving;

• provide opportunities for students to learn at more than one cognitive level.

Out-of-field teachers reported weak or moderate belief in their capabilities to provide learning environments described by these three items, whereas upskilled and in-field teachers reported strong or very strong beliefs for the same items.

6.3 Teacher Perceptions of Classroom Practices

Table 15.3 presents the six teachers’ responses to the TIMSS Grade 8 Teacher Questionnaire Mathematics, indicating how often they claimed to use the listed approaches when teaching their mathematics class. For five of the seven items, the reported frequencies increased from out-of-field to upskilled to in-field teachers, with upskilled and in-field teachers reporting similar frequencies for most approaches.

Table 15.3 Teacher’s perceived engagement in classroom practices

The most frequent approaches, endorsed by all three groups, involved:

• linking new content to students’ prior knowledge;

• asking students to explain their answers.

The least frequent approaches (shaded in Table 15.3), which also revealed the greatest differences between the perceptions of out-of-field and upskilled/in-field teachers, referred to:

• asking students to complete challenging exercises that require them to go beyond the instruction;

• encouraging classroom discussions among students;

• asking students to decide their own problem-solving procedures.

Out-of-field teachers reported that they either never used these approaches or only used these approaches in some classes. The upskilled and in-field teachers reported that they used these approaches for about half of the classes or in almost every class.

6.4 Observations of Classroom Practice

The mean scores on the Productive Pedagogies dimension for each group of teachers over the three lessons for which they were observed are shown in Table 15.4. Each mean score is calculated from six observations (2 teachers × 3 lessons). Looking down the columns of Table 15.4 reveals some similarities between the three groups of teachers: each group scored highest on the dimension of Supportive Environment and lowest on the dimension of Connectedness. The same pattern was found in Makar’s (2011) analysis of pedagogical practices in Australian primary school teachers’ ‘regular’ mathematics lessons.

Table 15.4 Productive pedagogies mean scores

Looking across the rows of Table 15.4 allows a comparison to be made between each of the three groups of teachers for each dimension of the Productive Pedagogies framework. In-field teachers were the group that achieved the highest mean score for the dimensions of Intellectual Quality and Supportive Classroom Environment. Upskilled teachers recorded the highest mean score for the dimension of Connectedness, with the mean score of the in-field teachers being very similar. Out-of-field teachers achieved the highest mean score for the Recognition of Difference dimension, largely due to significantly higher scores on the Inclusivity component of this dimension. This may be because they were the only teachers with mixed-ability, rather than ability-streamed, mathematics classes. It was observed that the out-of-field teachers placed particular emphasis on the element of Inclusivity within the dimension of Recognition of Difference by encouraging the participation of weaker students. Out-of-field T5 also paid particular attention to questioning and encouraging responses from female students, as in this class there was a tendency for male students to dominate the answering of questions.

Because the PDMT is mainly concerned with teaching mathematics for academic outcomes, its effects are most likely to be observed in teachers’ pedagogical practices corresponding to the academic dimensions of Intellectual Quality and Connectedness. Table 15.5 presents each teacher’s score totals for the three observed classes for each component of the dimension of Intellectual Quality. The maximum possible score total for each teacher is 15 (3 lessons × 5 points). Score totals instead of mean scores are presented for each component within the dimension for ease of comparison across the teachers and components.

Table 15.5 Intellectual quality score totals

The greatest differences between the groups of teachers within the dimension of Intellectual Quality occurred in Higher Order Thinking, Deep Knowledge and Problematic Knowledge (shaded in Table 15.5). The differences in the score totals between individual teachers for these components was at least 6 points across the three lessons or an average of 2 points per lesson on the 5-point observation scale. In general, the score totals increase from out-of-field to upskilled to in-field teachers.

According to the Productive Pedagogies classroom observation manual, Higher Order Thinking requires students to manipulate information and ideas in ways that transform their meaning and implications, which occurs when students combine facts and ideas in order to synthesise, generalise, explain, hypothesise or arrive at some conclusion or interpretation. Brief excerpts from lessons taught by T5 (out-of-field), T4 (upskilled) and T6 (in-field) are presented below to illustrate differences with respect to the quality of their questioning to necessitate student engagement in Higher Order Thinking. The excerpts represent typical practice of each teacher.

T5 (out-of-field) had used the analogy of a balance scale to show the method of solving an equation by ‘doing the same to both sides’ and thus maintaining the balance on both sides:

T5::

Now what happens if it is scales and I take 8 away from 12 on the right-hand side? What happens to the scales?

$\Delta + 8 = 12$

$\underline {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - 8}$

$\,\,\,\,\,\,\,\,\,\,\,\Delta = 4$

T5::

I’ll be left with 4. That side (points to right-hand side of equals sign) is now lighter than this side (points to left-hand side). This side (RHS) has only 4 on it and this side (LHS) has something plus 8. Remember both sides have to be equal. So whatever you do to one side of the scales you must do to the other side. So if I take 8 away from here as well (on LHS), we’ve cancelled them out so that means you’ve only your triangle left. So the triangle equals 4.

$\Delta + 8 = 12$

$\underline {\,\,\,\,\,\,\,\, - 8 = - 8}$

$\,\,\,\,\,\,\,\,\,\,\,\,\,\Delta = 4$

T5 then set the students to work individually on textbook exercises, and reconvened the whole class to check on their progress on solving the following equation:

$\square - 5 = 4$

T5::

How much is the square worth.

Student::

9

T5::

Is she right, is the square worth 9?

Many students::

Yes.

T5::

What did she do to both sides of the equation?

The final question asked by T5 only requires students to reproduce previously learned mathematical procedures and therefore does not elicit higher order thinking.

T4 (upskilled) was teaching students how to solve linear simultaneous equations. Student A had begun to solve a pair of equations as shown below:

$x + 2y = 7$

$\underline {2x + y = 8}$

$3x - y = 15$

A typical first step in solving simultaneous equations is to decide on a strategy for eliminating one of the variables. This is done by either adding or subtracting the equations (or a multiple of either or both equations that will give equal coefficients of either x or y). However, in this case, the student appears to have added x and 2x, but then subtracted y from 2y, and added 7 and 8. The following excerpt shows how T4 tried to find out what the student had done:

T4::

Student A we’ll start with you.

Student A::

So I plused the xs.

T4::

So 3x, I’m confused about what you did with the ys. Can you explain to me what you did?

Student A::

So I plused the x and the 2x and I got 3x and then y-2y is –y.

T4::

(continues with questions to guide Student A towards the correct procedure)

T4’s question (in bold type) asked Student A to explain, which is an instance of higher order thinking that manipulates rather than only reproduces information, as occurred in the previous example.

T6 (in-field) was also teaching students how to solve simultaneous equations. In the introductory lesson for this topic, he provided students with the following list of equations and asked:

T6::

Which of these equations do you think is the hardest to solve? Why?

• (1) $95x^2 - 2x + 105 = 0$

• (2) $3x + 2y = 8$

• (3) $9x^4 - 39x^3 + 9x^2 - 90x + 3035 = 0$

• (4) $\sqrt[4]{9x^4 } - \frac{9}{2}x^3 - 4^{5x} - 87x = 0$

Through further questioning of individual students, T6 elicited the conclusion that Eq. (2) is the most difficult to solve because it has two variables and, in fact, this equation has an infinite number of solutions. However, it is possible to find values of x and y that satisfy two equations of this type simultaneously. T4’s question requires a high level of higher order thinking on the part of students, because they must synthesise several pieces of prior knowledge about what it means to solve an equation in order to arrive at and justify a conclusion.

To summarise, higher order thinking is necessary to answer the question posed by T6 and is required to some extent to answer the question posed by T4; however, the questions posed by T5 mainly require the students to rehearse mathematical procedures.

The differences between teacher groups were considerably less for the dimension of Connectedness (Table 15.6); this may be due to the lower score totals obtained by all three groups. The main difference in this dimension occurred for the component of Problem-Based Curriculum (shaded in Table 15.6), with the difference being equivalent to at least 3 points across the three lessons, or a mean of 1 point per lesson on the 5-point observation scale. The Problem-Based Curriculum component refers to the extent to which students are presented with real, practical or hypothesised problems to solve, including the recognition of the connection between classroom knowledge and situations outside the classroom with the exploration of these connections to create significance for the knowledge.

Table 15.6 Connectedness score totals

The Productive Pedagogies classroom observation manual defines a problem as a task with no specified correct solution that requires knowledge construction on the part of students. In keeping with the mathematics education research literature, we re-interpreted this definition to mean that a mathematical problem is a task for which the student does not know and needs to construct the solution method (National Council of Teachers of Mathematics, 2000). The following brief excerpts from lessons taught by T3 (out-of-field), T1 (upskilled) and T2 (in-field) illustrate differences in how these teachers engaged students in a problem-based curriculum. The excerpts were chosen because they represent typical practice of each teacher.

T3 (out-of-field) was teaching the class how to perform the algebraic manipulations of expanding and simplifying. She began with a numerical example and showed two solution methods, the second of which involved use of the distributive law, the algebraic procedure she wished the students to learn:

$4(3 + 2)$

Two methods: $4\left(5\right)=20$ and

$4(3) + 4(2) = 12 + 8 = 20$

She then asked students to expand $4(x+2)$. As students were expected to mimic the solution method that had been demonstrated by the teacher, this task is not classified as a problem and so there is no evidence of a problem-based curriculum in this excerpt.

T1 (upskilled) was introducing the topic of patterns and relationships as part of the study of algebra. He posed the following task:

T1::

If I gave you this pattern here: x, y, z, x, y, z, x, y, z, … What letter is in the 63^rd position?

Student A::

z

T1::

Why z?

Student A::

Because 3 goes into 63 evenly.

This was a fairly straightforward, but nevertheless unfamiliar, task for which the students needed to construct a solution method based on the recurring x, y, z pattern.

T2 (in-field) was introducing Pythagoras’ Theorem, which specifies the relationship between the side lengths of any right-angled triangle: the area of the square on the hypotenuse (the longest side) is equal to the sum of the areas of the squares on the other two sides. This relationship can be written algebraically as ${a}^{2}+{b}^{2}={c}^{2}$, where c represents the length of the hypotenuse and a and b the lengths of the other two sides. Instead of just giving the students this formula, T2 had the students construct a right-angled triangle with side lengths of 6, 8 and 10 units and draw the squares on all three sides (see Fig. 15.2). Because the triangle was drawn on graph paper, it was easy to count the small ‘boxes’ in the squares on the two shorter sides to arrive at a measure of their areas. However, because of the orientation of the square on the hypotenuse, this counting of ‘boxes’ was not straightforward, so the teacher and students negotiated an estimation strategy that involved counting all the ‘full boxes’ and then combining ‘half boxes’ to complete the count. This was a genuine problem for which several alternative solution methods were possible.

Fig. 15.2

Investigating Pythagoras’ theorem

Thus, there is some evidence that the kind of knowledge construction that characterises a problem-based curriculum is called for in the tasks offered by T2 and T1, while the task set by T3 instead requires using well-defined algorithms for algebraic manipulation.

7 Discussion

This study contributes to our larger research agenda for investigating the impact of the Professional Diploma in Mathematics for Teaching, a large-scale professional development programme for out-of-field teachers of mathematics. To date, our research has relied on teacher self-reports (Goos et al., 2019; O’Meara & Faulkner, 2021), assessments of teacher knowledge (Ní Ríordáin et al., 2017) or analyses of teachers’ action research reports (Lane & Ní Ríordáin, 2019) to gather evidence of the programme’s impact. Some of these studies collected data on self-reported beliefs and classroom practices before and after teachers experienced components of the PDMT (e.g. pedagogy workshops, action research), while others interpreted the self-reported beliefs and classroom practices of PDMT graduates in the light of international mathematics education research literature. In this chapter, for the first time, we report on direct observation of the classroom practices of PDMT graduates.

While we would have liked to observe lessons taught before and after participating teachers had completed the PDMT in order to make stronger claims about the programme’s impact, logistical constraints make it very challenging to implement such research designs. Instead, we adopted a multiple-case study design to seek insights into ‘a contemporary phenomenon within its real-life context’ (Yin, 2003, p. 13): the classroom practices of these upskilled teachers, teachers who were still teaching mathematics out-of-field and qualified teachers of mathematics who had always been in-field. We focused on three aspects of practice: teacher beliefs about their capability to perform specific teaching tasks (self-efficacy beliefs), teacher perceptions about their classroom practices (perceived practices) and structured independent observations of teachers’ actual classroom practices (observed practices).

7.1 Insights into Self-Efficacy Beliefs and Classroom Practices of Out-of-Field, Upskilled and In-Field Teachers of Mathematics

There were clear differences between the self-efficacy beliefs of the out-of-field teachers, on the one hand, and the upskilled and in-field teachers, on the other hand. Upskilled and in-field teachers resembled each other in reporting stronger self-efficacy beliefs than out-of-field teachers in relation to their capabilities of actively involving students in developing concepts, engaging in critical thinking and/or problem-solving and in providing opportunities for students to learn at more than one cognitive/performance level. The upskilled and in-field teachers, more so than the out-of-field teachers, also perceived that they made more frequent use of teaching practices that ask students to complete challenging tasks, engage students in discussion and encourage students to decide their own problem-solving procedures. These perceptions of classroom practice may indicate that out-of-field teachers are less comfortable using teaching approaches that invite students to go beyond the limits of the teachers’ own content knowledge. All teachers claimed that they linked new content to students’ prior knowledge in at least half the lessons they taught; however, evidence from the lessons that were observed suggests that connections were made to students’ school knowledge of the topic rather than to any out-of-school experiences that might enhance their understanding of the new material.

With respect to the classroom observations, the groups of teachers were similar in that they all scored highest on Supportive Classroom Environment and lowest on Connectedness, a finding that aligns with previous research into mathematics teaching using the Productive Pedagogies framework (Makar, 2011). Some of the differences between the groups suggested that the upskilled teachers (graduates of the PDMT programme) may be adopting pedagogical practices that are more like those of in-field teachers than those who are still teaching mathematics out-of-field, especially in relation to the provision of intellectual quality and connectedness.

7.2 Insights into Evidencing the Impact of Professional Development

Desimone’s (2009) conceptual framework for studying teacher professional development provided a useful heuristic for planning our research into the impact of the PDMT. She wrote that classroom observation and teacher self-reports are commonly used methods for measuring the effects of professional development. She further argued that both methods can provide valid data if the same observer uses a well-constructed protocol for all classroom observations and the teacher self-report protocol focuses on what teachers did rather than how well they did it. In our study, a single observer used the Productive Pedagogies observation protocol to ensure a consistent approach to gathering and analysing data on teachers’ classroom practices. The teacher self-report instruments asked teachers about the strength of their self-efficacy beliefs and the frequency of implementing the nominated teaching approaches, thus avoiding evaluative judgments as recommended by Desimone.

A challenge for research into teacher change is the possibility of social desirability bias, which ‘can occur in any form of data collection’ (Desimone, 2009, pp. 189–190), whether this involves surveys, interviews or observations. Such biases can be avoided by using well-constructed instruments that are aligned with a study’s research questions and administered appropriately. We suggest that, additionally, data collection instruments that combine teacher self-report with independent observation need to be aligned so that they tap into the same, or similar, underlying constructs. For example, many of the items that were used in the Teacher Efficacy Beliefs Survey (see Table 15.2) refer to teacher beliefs in their abilities to engage students in developing concepts, higher order thinking, critical thinking and problem-solving—all of which strengthen the intellectual quality of a lesson as defined by the Productive Pedagogies protocol. Similarly, the TIMSS Grade 8 Teacher Questionnaire Mathematics elicits teacher perceptions of the frequency of classroom practices such as encouraging student discussion, offering challenging tasks (both of which align with intellectual quality) and relating lessons to students’ prior knowledge and daily lives (aligned with connectedness, another of the Productive Pedagogies dimensions). It would be beneficial for future research into the impact of the PDMT to conduct a more detailed mapping of alignment between the data collection instruments used in the present study.

8 Conclusion and Recommendations

The conclusions that we draw from this study can only be tentative, given the small sample and case study design. A case is not a sample from which one can generalise to a population; however, case study findings permit analytic generalisation in order to expand the theories upon which the study was based (Yin, 2003). Our findings suggest that the structured lesson observation provided by the Productive Pedagogies framework may be useful in supplementing the upskilled teachers’ self-reported changes in their pedagogical practices arising from participation in a professional development programme. In addition, such structured observations may usefully inform the design of programmes aimed at developing out-of-field teachers’ (and also pre-service teachers’) knowledge of mathematics and pedagogical practices, particularly in pinpointing specific items within the academic outcomes of schooling that require further consideration (e.g. knowledge integration and connectedness beyond the classroom).

Two recommendations arise from the findings of the present study, and the broader research programme that is investigating the impact of the PDMT. Firstly, research into the effectiveness of professional development programmes for out-of-field teachers should be guided by a conceptual framework that operationalises how such programmes influence teacher learning and, ultimately, the improvements to student learning that are claimed to result. We used Desimone’s (2009) path model, but other frameworks exist (e.g. see Clarke & Hollingsworth, 2002; Guskey, 2000). The second recommendation is directed at education policy makers who may fund professional development programmes for out-of-field teachers. While such investment in teacher development is welcome, significant funding is also needed to gather evidence of the impact of these programmes, and especially in terms of changes to teachers’ classroom practices. Large-scale classroom observation studies are rare and costly (see, Lingard et al., 2001, for an example), but can reveal trends that support further policy and practice initiatives. Our own study, while involving only a small number of participants, offers insights into the knowledge that can be gained from classroom-based research with newly upskilled teachers of mathematics.