Collective Motion of Atoms in Metals by First Principles Calculations

Abstract

Fundamental information on the collective motion of atoms can be learned by tracing imaginary phonon modes in deformed crystals. This should be useful to investigate the atomic process of plaston in a logical manner. Here, we summarize our works on the collective motion of atoms in unary metallic crystals examined by first principles phonon calculations. A simple algorithm for automated searching of the structural transition pathway following the imaginary phonon modes has been constructed. We first show the construction of structure evolution diagrams in Cu, Mg, Ti, and Hf by taking a simple cubic (SC) structure as a starting structure. The pathway corresponds to a route connecting initial and final structures without any energy barrier. Effects of the hydrostatic pressure on the diagram have been examined as well. In the second part, the collective motion of atoms in HCP-Ti under homogeneous shear deformation corresponding to the {$10\overline{1} 2$} twinning mode is shown. The structural transition pathway from the parent to twin, which is widely accepted as the “shuffling”, is shown in detail.

1 Introduction

The plaston concept has been proposed recently in order to explain interesting plastic deformation behaviors that appear in some ultrafine grained metals or bulk nanostructured metals (BNM). They show both high strength and large tensile ductility contrary to the general trade-off relationship between strength and ductility in metals (Tsuji and Ogata et al. 2020). Normal dislocation mode is predominant in the early stage of plastic deformation of ordinary metals. Sequential nucleation of different deformation modes, such as unusual dislocation modes, deformation twinning, and martensitic transformation, would induce strain-hardening ability of such BNMs, leading to high strength and large ductility.

Collective motion of atoms occurs under a stress field in materials leading to nucleate various plastic deformation modes that are not only dislocation glide but also deformation twinning and martensitic transformation. The atomic process of plastic deformation is called plaston. A logical way to scrutinize the collective motion of atoms is given by systematic calculations tracing imaginary phonon modes in deformed crystals. Although nucleation of plastic deformation modes in polycrystalline materials predominantly takes place at grain boundaries and other crystalline imperfections where atomic arrangements are irregular and stress field is complicated, we have started our calculations on perfect crystals in order to study the collective motion of atoms in a simple way. Firstly, we will show the collective motion of atoms associated with the phase transition in metallic elements (Togo and Tanaka 2015a). A simple algorithm for automated searching of the phase-transition pathway following the imaginary phonon modes is presented. Secondly, the collective motion of atoms in HCP-Ti under homogeneous shear deformation corresponding to the {$10\overline{1} 2$} twinning mode (Togo et al. 2020) will be shown.

2 Phase-Transition Pathway in Metallic Elements

The phase-transition pathway (PTP) connects structures before and after the phase transition by continuous atomic displacements and lattice deformation. In the past, PTP was searched via group-subgroup relationships of crystal structures choosing a limited number of pathways. The energy change along the PTP was not examined. Consequently, the resulted pathways were not necessarily realistic.

The PTPs can be unambiguously examined by a combination of the first principles calculations and the symmetry analysis. Although the PTP can be started from an arbitrarily chosen crystal structure, the starting crystal is better to have high symmetry and high energy. In the study described in Togo and Tanaka (2015a), we took a simple cubic (SC) structure as the start. For the first principles calculations, the plane-wave basis projector augmented wave method (Blöchl 1994) within the framework of density functional theory (DFT) as implemented in the VASP code (Kresse Non-Cryst 1995; Kresse and Furthmüller 1996; Kresse and Joubert 1999) was employed. Dynamical matrices of a given crystal were firstly obtained by the first principles phonon calculation using the phonopy code (Togo and Tanaka 2015b). The dynamical stability of the crystal was investigated by the eigenvalues of the dynamical matrices. The square root of the eigenvalue is the phonon frequency. The negative eigenvalue, i.e., the imaginary phonon frequency indicates the dynamical instability. If the sign of the instability was found, the structure was deformed along the direction indicated by the eigenvector of the unstable eigensolution that provides information of collective displacement of atoms to break the crystal symmetry minimally. In this manner, the symmetry constraint was removed, and the geometry of the structure could be further relaxed. Since it is difficult to relax the structure strictly to the local minimum of the potential energy surface at which high crystal symmetry may recover, the relaxed structure was cast in one of space group types accepting a predetermined tiny tolerance. The procedure was repeated by returning to the phonon calculations of the relaxed structure. When there were multiple instabilities, the procedure was split into multiple branches. Finally, the set of the connections produced a line diagram as shown in Fig. 4.1 for Cu and Mg.

Fig. 4.1

Adapted from Togo and Tanaka (2015a) with small modification (CC BY 3.0)

Structure evolution diagrams showing phase-transition pathway (PTP) of a Cu and b Mg. Phonon band structure of simple cubic (SC) Cu is shown in the inset. Open and filled symbols, respectively, represent dynamically unstable and stable crystal structures.

Instabilities of phonon were found at the wave vectors of M and X points for SC-Cu as shown in the inset (phonon band structure) of Fig. 4.1. The deformation at the M point broke the symmetry of the SC structure (Pm$\overline{3}$m) to P4/nmm. The twofold degenerated instability at the X point led to Pmma and Cmcm. A calculation unit was defined as a set of procedures from one phonon calculation including relaxation of the input crystal structure to the creation of deformed crystal structures following the dynamical instabilities. The deformed crystal structures were used as the input of the next units. The next units were processed in the same way. The deformed crystal structure of P4/nmm was relaxed to the body-centered tetragonal (BCT) structure. Pmma and Cmcm were relaxed to simple hexagonal (SH) and face-centered cubic (FCC) structures, respectively. If no instability was found in a unit, this unit ended. The unit of Cmcm formed no next unit since FCC was dynamically stable for Cu. The whole procedure finished when all crystal structures of the end-point units became dynamically stable.

In Fig. 4.1, PTPs are shown by thick (blue) lines. The line was drawn only when the final structures were made by continuous atomic displacements and lattice deformation of the initial structure. The common subgroup of initial and final structures was written vertically next to the line. The energy decreased monotonously with the phase transition along the line, meaning that the transition can occur without an energy barrier. The line ended when the final structure became dynamically stable.

In this study, the supercell size was limited in order to search for simple PTPs. The explosion of the computational demands can then be avoided. Both of the 3 × 3 × 2 and 2 × 2 × 2 supercells were used to calculate force constants for the hexagonal primitive cells, and the 2 × 2 × 2 supercells were used for the other primitive cells. If the length of a supercell lattice vector exceeded 20 Å, the primitive cell was no more expanded in this direction. The elastic instability was calculated by introducing strains to the crystal structures. However, we did not find any different crystal structures from those found without considering the elastic instability. The freedom of elastic instabilities was not included for the simplicity of the algorithm.

We can find some similarities and differences between diagrams of Cu and Mg. HCP is lower in energy than FCC in Mg, which is consistent with the fact that Mg forms HCP under ordinary conditions. 9R structure (R$\overline{3}$m), known as the samarium structure, is one of the long-period-stacking (LPS) structures with ABABCBCACA stacking of the close packed planes. The diagram shows that the 9R structure is formed from the Cmmm structure via P$\overline{2}$/c. The structural relationships of the FCC and 9R structures to the Cmmm are shown in Fig. 4.2. Another LPS structure, 18R, is found in the diagram of Mg. Both 9R and 18R structures are experimentally known to be formed in Mg alloys.

Fig. 4.2

Adapted from Togo and Tanaka (2015a) with small modification (CC BY 3.0)

Crystal structures of FCC, Cmmm, and 9R structures. Thick lines show the edges of the conventional unit cells. The conventional unit cell of the Cmmm structure is doubled along both of a and b axes to show the correspondence between Cmmm and 9R structures.

Diagrams for two HCP metals, Ti and Hf, are displayed in Fig. 4.3. As expected, HCP shows lower energy than FCC. Two diagrams look similar. But, the path connecting SH and ω is absent in Ti, which implies that there is an energy barrier in the SH → ω path. The SH → ω path can be seen both in Cu and Mg (Fig. 4.1) and also in Hf. We made a separate set of calculations for the ω structure of 27 transition elements. (Ikeda and Tanaka 2016) ω-Ti is dynamically stable and the energy is lower than HCP. ω-Ti was experimentally reported to be existent under the external pressure of 2 GPa at 293 K (Sikka et al. 1982). The critical pressure decreases with decreasing temperature by approximately dT/dp = 100 K/GPa (Sikka et al. 1982), which suggests that ω is more stable than HCP at temperatures <90 K. However, a large hysteresis was experimentally reported for the transition between HCP and ω under pressure. The HCP → ω transition has not yet been reported experimentally under the ordinary pressure. The presence of a large energy barrier between SH and ω is implied by these experimental results. The absence of the SH → ω path in Fig. 4.3a is consistent with the experimental reports.

Fig. 4.3

Adapted from Togo and Tanaka (2015a) with small modification (CC BY 3.0)

Structure evolution diagrams of a Ti and b Hf.

Pressure effects on the structure evolution diagram can also be examined in the same way as described above. Figure 4.4 shows the result for Cu under 30 GPa of hydrostatic pressure. Note that the vertical axis shows relative enthalpy here. As compared to the zero-pressure case shown in Fig. 4.1a, the number of dynamically stable phases increased under 30 GPa. BCC-Cu became dynamically stable. The formation of BCC-Cu was experimentally reported in the initial process precipitation in Fe-Cu alloys (Othen et al. 1994). Three LPS structures, i.e., 9R, 12R, and 18R appeared under 30GPa, similar to the case of Mg (0 GPa). The 9R-Cu was experimentally reported as a thin layer of the Σ3 grain boundary in Cu (Wolf and Ernst 1992) and in severely deformed Cu single crystals (Dymek and Wróbel 2003).

Fig. 4.4

Adapted from Togo and Tanaka (2015a) with small modification (CC BY 3.0)

Structure evolution diagram of Cu at 30 GPa.

3 HCP-Ti Under Shear Deformation Along Twinning Mode

Figure 4.5a shows the conventional unit cell of HCP-Ti. In order to represent the {$10\overline{1} 2$} twinning mode, the unit cell is retaken by using η₁ and η₂ directions and K₁ and K₂ planes as shown in Fig. 4.5b. P (green) is the shear plane. Symmetry constraints are given to distinguish four structures, i.e., the parent, sheared-parent, shuffling, sheared-twin, and twin structures. Three structures are shown in Fig. 4.5c–e. The parent and twin structures have the space group type of P6₃/mmc. The sheared-parent structure has the space group of C2/m in general. It becomes Cmcm only when the sheared lattice becomes the same lattice as the parent in a different orientation. The shuffling structure appears during the transformation from the sheared-parent to sheared-twin structures.

Fig. 4.5

Adapted from Togo et al. (2020) with small modification (CC BY 3.0)

a The conventional unit cell of HCP-Ti. b An extended unit cell to represent the {$10\overline{1} 2$} twinning mode of HCP-Ti. The twinning mode is characterized by K₁ (red) and K₂ (blue) planes and η₁ and η₂ directions. Structures of an extended unit cell of c parent, d sheared-parent, and e twin. The atoms with the same symbols (open or filled) are located on the same plane parallel to the plane P. Two planes with the open and filled symbols are separated by 0.5b′ each other.

Atomic positions of the sheared-parent structures were optimized under the symmetry constraint. Shears were sampled to 21 points within 0 ≤ s/s_t ≤ 1, where s/s_t denotes homogeneous shear, s, normalized by the twinning shear, s_t. In order to introduce homogeneous shear, the positions of atoms have to be properly set since there are degrees of freedom to relax atomic positions under symmetry constraints. We defined atomic displacement u(s/s_t) as the difference between the atomic positions after and before the relaxation. The initial position before the relaxation was given keeping the crystallographic coordinates of the HCP unit cell. The displacement distances |u(s/s_t)| with respect to s/s_t are shown in Fig. 4.6. Since |u(s/s_t)| of all atoms in the unit cell at given s/s_t are the same, only one value at each s/s_t is shown. In the inset, the directions of the displacements are shown. In this figure, only two directions that are directed in the opposite directions can be seen. The atoms having the same displacement directions are symmetrically equivalent by the lattice translation. The displacement distance |u(s/s_t)| increases with s/s_t. Even at s/s_t = 1, |u(s/s_t)| is only 4% of the nearest neighbor distance. Therefore, for the schematic analysis, this optimization process is unimportant, although it is necessary to perform phonon calculations accurately.

Fig. 4.6

Adapted from Togo et al. (2020) (CC BY 3.0)

Displacement distance, |u(s/s_t)|, for the {$10\overline{1} 2$} twinning mode as a function of s/s_t. In the inset, the sheared-parent structure at s/s_t = 1 before the optimization is shown. The arrows show the approximate directions of the displacements.

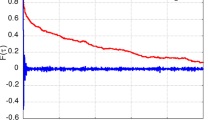
In Fig. 4.7, the electronic total energy of the sheared-parent structure is shown as a function of the homogeneous shear s/s_t. With increasing the shear, the energy increases harmonically. According to the definition of the deformation twinning, the sheared-twin structures should have the same energy curve with respect to 1 − s/s_t, which is drawn as the mirror image of the energy curve of the parent (dotted curve in Fig. 4.7). The presence of the crossing of the energy curves at s/s_t = 0.5 means that their energy surfaces are disjoined under the symmetry constraint of C2/m.

Fig. 4.7

Adapted from Togo et al. (2020) (CC BY 3.0)

Energy increases per atom of the sheared-parent structures for the {$10\overline{1} 2$} twinning mode. The dotted curve is the mirror image of the energy curve of the sheared-parent structure representing the energy increases of the sheared-twin structures. The vertical dashed arrows indicate energies released by the transformation from the sheared-parent to the sheared-twin structures. The inset shows the sheared-parent structure at s/s_t = 1. The displacement directions indicated by the eigenvector of the imaginary phonon mode at M′(1/2, 0, 0) are shown by thick arrows.

The sheared-parent structure transforms to the sheared-twin structure spontaneously by breaking the symmetry constraint at s/s_t > 0.5. The phonon band structures at six s/s_t are shown in Fig. 4.8. One phonon mode at M′(1/2, 0, 0) clearly shows the imaginary frequency at large shears, which implies that spontaneous structural transformation should occur by breaking the symmetry. By plotting the squared frequencies at M′(1/2, 0, 0) with respect to the homogeneous shear s/s_t, the critical shear to induce the spontaneous structural transformation can be estimated to be s/s_t ~ 0.68.

Fig. 4.8

Adapted from Togo et al. (2020) (CC BY 3.0)

A series of phonon band structures corresponding to the {$10\overline{1} 2$} twinning mode at s/s_t = 0, 0.2, 0.4, 0.6, 0.8, and 1. Those at different s/s_t are drawn by the different line styles from solid to shorter dashed lines. In vertical axis, phonon frequency lower than zero denotes imaginary frequency. Wave vectors are labeled as A′(0, 0, 1/2), H′(1/3, 1/3, 1/2), K′(1/3, 1/3, 0), Γ(0, 0, 0), M′(1/2, 0, 0), and L′(1/2, 0, 1/2). Although the homogeneous shear breaks the crystal symmetry, we adopt the same labels for points in the Brillouin zones for easy comparison. Since the shapes of the Brillouin zones are different for the different shears, the positions of the reciprocal points in the Cartesian coordinates measured from the Γ points disagree slightly. The filled circles at the M′ points indicate the soft phonon modes that have the eigenvector drawn in the inset of Fig. 4.7.

The eigenvector of the soft phonon mode at M′(1/2, 0, 0) as illustrated in the inset of Fig. 4.7 indicates the information on the collective atomic displacements to properly break the symmetry of the crystal. The arrows indicate the direction of displacement of the atoms with the same relative amplitude. The breaking of symmetry expands the primitive cell twofold. The space group type then becomes P2₁/c (No. 15). The sheared-parent structure models were generated by introducing minimum finite displacements along the directions as described above, so that the first principles calculation code, VASP, can properly detect the broken symmetry. Then, the first principles calculations were made to optimize these structure models at given homogeneous shears fixing their basis vectors. After the structure optimizations, the sheared-twin structures at s/s_t = 0.7 to 0.95 and the twin structure at s/s_t = 1 were obtained. This is the shuffling that we consider. The atomic displacements by this transformation at s/s_t = 1 are shown by short black arrows in Fig. 4.9. The displacement distance is roughly constant by ~0.5 Å (17% of the interatomic distance) at all s/s_t larger than the critical shear. Four atoms are involved in the collective displacement as the minimum unit. Two types of parallelogram units by alternately changing their rotation directions depicted by red circular arrows are arranged to fill the crystal structure. The spaces surrounded by these rotating units behave as if they were breathing. In this manner, the internal structural distortion is considered to be minimized. This figure is similar to the one obtained by Crocker and Bevis reported in 1970 (Crocker and Bevis 1970) for the shuffling of the {$10\overline{1} 2$} twinning mode from the crystallographic discussion. In this study, we found that the shuffling necessarily occurs at a shear larger than the critical value based on the first principles calculations.

Fig. 4.9

Adapted from Togo et al. (2020) (CC BY 3.0)

Displacements of atoms induced by the structural relaxation from the sheared-parent structure (Fig. 4.5d) to the twin structure (Fig. 4.5e) depicted as the short black arrows. The circular red arrows depict how the displacements are arranged as units.

The vertical dashed arrows in Fig. 4.7 correspond to the energy between the sheared-parent and sheared-twin structures, which is released by the shuffling. The presence of a potential energy barrier may prevent the initiation of the shuffling between s/s_t = 0.5 and the critical shear s/s_t ~0.68. When crystalline imperfections are present, as in a real material, the potential energy barrier may be lowered locally, and the shuffling initiated from the imperfection may propagate over the macroscopic range to result in the macroscopic twinning. Once the shuffling is locally initiated, the sheared-parent may relax toward the twin instantaneously. Although it would be difficult to observe the initiation of the twin at an atomic level, evidence of the shuffling mechanism may be experimentally obtained by measurement of the frequency change of the characteristic phonon mode at s/s_t < 0.5 by inelastic neutron or X-ray scattering techniques.