1 Introduction

Ultra-stable lasers with high-frequency stability and phase coherence are indispensable as fundamental tools in the field of precision spectroscopy measurement science, optical atomic clocks, gravitational wave detection, ultralow phase noise optical or microwave synthesis and fundamental physics tests [1,2,3,4,5,6,7,8]. In the last two decades, the development of ultra-stable lasers with high-frequency stability and phase coherence has never been suspended. State-of-the-art ultra-stable lasers are usually realized by stabilizing laser frequency to an ultra-high-finesse Fabry–Pérot (FP) cavity using the Pound–Drever–Hall (PDH) method. Although this approach can achieve a level of frequency stability below \(1\times {10}^{-16}\) [9, 10], it requires precise mode matching, alignment of free-space-optical elements, precise temperature control or even cryocooler, and thus the system is bulky and complex. Therefore, it is difficult to meet the requirements in the transportable applications, such as optical atomic clock for geodesy [6] and gravitational wave detection in space [11,12,13]. In this letter, as a simple and compact alternative, fiber-delay-line (FDL) stabilized lasers are reported.

2 Material and Methods

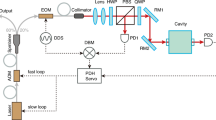
In Fig. 35.1a, an arm-unbalanced optical fiber interferometer is used as a frequency discriminator to convert the frequency fluctuation (\(\Delta \nu \)) of the laser into the phase fluctuation (\(\Delta \varphi \)). The phase fluctuation is then detected and fed to the laser for frequency stabilization. The transfer function of the interferometer can be defined by

$$\varGamma \left(f\right)=\frac{\Delta \varphi \left(f\right)}{\Delta \nu \left(f\right)}=\frac{1-{\mathrm{e}}^{-2\pi if\tau }}{\mathrm{i}f}$$
(35.1)

where f is the Fourier frequency, \(\tau \) is the unbalanced time delay of the interferometer which can be written as \(\tau =2nL/c\), n is the effective refractive index of optical fiber, L is the length difference between the two arms of the interferometer, and c is the speed of light in vacuum. At low frequencies \(\left(f\ll 1/\tau \right)\), the transfer function can be approximately equal to the follows

$$\varGamma \left(f\right)=\frac{1-{\mathrm{e}}^{-2\pi if\tau }}{\mathrm{i}f}\approx 2\pi \tau $$
(35.2)
Fig. 35.1
figure 1

a Principle of FDL laser stabilization and b transfer function of the interferometer

Full size image

The transfer function is plotted in magnitude in Fig. 35.1b. The transfer function has a series of zeros at the frequencies of \(n/\tau \) (\(n=1, 2, 3\dots \)) and the first one limits the bandwidth of the control loop of the laser frequency stabilization. At low frequencies (\(f\ll 1/\tau \)), the transfer function is approximately equal to \(2\pi \tau \), which means a longer fiber increases the gain of the discriminator while reduces the bandwidth of the control loop. In general, a compromise is required between the bandwidth of the control loop and the gain of the discriminator.

Recently, the FDL laser frequency stabilization has been demonstrated to achieve a sub-hertz linewidth ultra-stable laser [14,15,16]. Compared to the FP cavity method, this approach can provide not only agile frequency tunability, but also compactness, high reliability, small volume, and light weight [17]. These advantages make it possible to develop a miniaturized transportable ultra-stable laser. However, this approach is sensitive to temperature fluctuation. To migrate this problem, a delicate thermal shield system is required. Besides, an ultralow vibration sensitivity optical fiber spool is used to reduce the excess frequency noise induced by mechanical vibration.

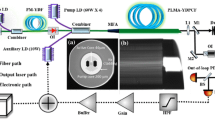
The scheme of the laser frequency stabilization is shown in Fig. 35.2. A 1550 nm DFB fiber laser (NKT photonics) is used as the laser source. The laser beam passes through an acousto-optic modulator (AOM1) before going to an unbalanced Michelson interferometer, and then is split into two parts by an optical coupler with a coupling ratio of 99:1. The small part is sent to the interferometer for laser frequency stabilization while the large one is used as the laser output. In the interferometer, another acousto-optic modulator (AOM2) is inserted into the long arm to produce a radio frequency (RF) shift for heterodyne detection. The output of interferometer is connected to a photodiode, yielding a RF beat note signal. This signal is then demodulated by a tunable synthesizer to produce the error signal. A proportional-integral servo circuit converts the demodulated error signal into the correction signal which simultaneously acts on a piezo-electric transducer (PZT) stretcher and a voltage-controlled oscillator driving the AOM1.

Fig. 35.2
figure 2

The scheme of the laser frequency stabilization system. PZT: piezo-electric transducer; AOM: acousto-optic modulator; VCO: voltage-controlled oscillator; RF: radio frequency

Full size image

In this scheme, the optical fiber is sensitive to the temperature fluctuation that can cause a long-term frequency instability. Therefore, the temperature stabilization of the optical fiber is of importance. The temperature fluctuations mainly come from (1) cabinet environmental temperature fluctuation; (2) optical power fluctuation; (3) RF signal power fluctuation. To migrate these problems, we adopt several modifications on the system described in our previous work [18]. First, a four-layer thermal shields are used (shown as Fig. 35.3). Each layer of the shields is treated by polishing and gold-plating to reduce their emissivity. The solar absorptivity of the shield surface is about \(0.3\) while the emissivity is about \(0.03\). Using a finite-element-method analysis, the calculated thermal time constant is about 20 days. Second, a two-stage active temperature stabilization is employed in this experiment and the temperature fluctuation of the outer shield is small than \(0.5\mathrm{ mK}\) over a time of 24 h. Third, both the optical power injecting into the interferometer and the RF power driving the AOM1 are stabilized. Last but not least, to reduce the size of the laser stabilization system, a miniature optical fiber spool with low vibration sensitivity is designed and its volume is small than \(1.7 L\). The measured vibration sensitivity on the radial and axial direction is about \({3\times 10}^{-11}/g\) and \({8\times 10}^{-11}/g\), respectively, for a frequency range of 20–200 Hz [19]. The whole volume of the assembled laser stabilization system is about \(5.0 L\).

Fig. 35.3
figure 3

a Schematic of the vacuum chamber and b its practicality picture

Full size image

3 Results and Discussion

We construct two identical laser systems to evaluate the performance of the ultra-stable laser. Each laser is constructed using a separate fiber laser source, a separate fiber interferometer, a separate temperature control system, and separate electronics. Furthermore, both systems are identical and their contributions to the measurements can be considered as the same. The experimental setup used to measure the laser frequency stability is shown in Fig. 35.4. The light beams of the two stabilized lasers are combined by an optical fiber coupler and a heterodyne beat-note signal of approximate 160 MHz is detected by a photodiode. The frequency drift of the beat-note signal is compensated to less than 0.1 Hz/s by applying a small frequency offset to the tunable RF synthesizer [16].

Fig. 35.4
figure 4

Simplified diagram of the experimental setup. Optical paths are in solid, electrical in dotted line of dark. LPF: Low Pass Filter

Full size image

The beat-note signal is then sent to a time interval analyzer (Symmetricom 5125A) for frequency comparison against a reference signal from an active hydrogen maser (iMaser3000, T4Science). The recorded phase data from the time interval analyzer are then used to calculate the frequency stability of the two lasers. For one laser, the calculated frequency stability should be divided by \(\sqrt{2}\). The measured frequency stability for a single system is shown in Fig. 35.5. In the time scale of 1–128 s, the frequency stability is better than \(5\times {10}^{-15}\). The ascending trend at long-term time scale is mainly due to the residual temperature fluctuations or laser intensity fluctuations.

Fig. 35.5
figure 5

Fractional frequency stability of all-fiber-based ultra-stable laser systems

Full size image

4 Conclusions

In conclusion, we demonstrate an all-fiber-based miniaturized transportable ultra-stable laser with a medium-term frequency stabilization of below \(5\times {10}^{-15}\) in the time scale of 1–128 s. In future work, a more stable temperature control system should be further investigated to improve the long-term frequency stability.